When I was maybe five or six years old, my mother (a distinguished teacher) said to me about problem solving, more or less: if you can draw a picture of a problem-situation, you can understand it well enough to solve it.
Over the many years since, that has served me well.
Where, after so many months of debates over FSCO/I and/or CSI, I think many of us may well be losing sight of the fundamental point in the midst of the fog that is almost inevitably created by vexed and complex rhetorical exchanges.
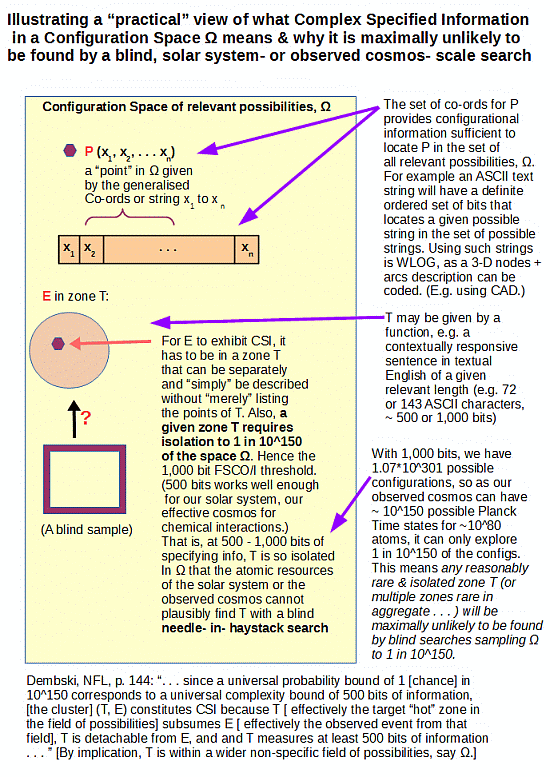
So, here is my initial attempt at a picture — an info-graphic really — of what the Complex Specified Information [CSI] – Functionally Specific Complex Organisation and/or Information [FSCO/I] concept is saying, in light of the needle in haystack blind search/sample challenge; based on Dembski’s remarks in No Free Lunch, p. 144:
 Of course, Dembski was building on earlier remarks and suggestions, such as these by Orgel (1973) and Wicken (1979):
Of course, Dembski was building on earlier remarks and suggestions, such as these by Orgel (1973) and Wicken (1979):
ORGEL, 1973: . . . In brief, living organisms are distinguished by their specified complexity. Crystals are usually taken as the prototypes of simple well-specified structures, because they consist of a very large number of identical molecules packed together in a uniform way. Lumps of granite or random mixtures of polymers are examples of structures that are complex but not specified. The crystals fail to qualify as living because they lack complexity; the mixtures of polymers fail to qualify because they lack specificity. [The Origins of Life (John Wiley, 1973), p. 189.]
WICKEN, 1979: ‘Organized’ systems are to be carefully distinguished from ‘ordered’ systems. Neither kind of system is ‘random,’ but whereas ordered systems are generated according to simple algorithms [i.e. “simple” force laws acting on objects starting from arbitrary and common- place initial conditions] and therefore lack complexity, organized systems must be assembled element by element according to an [originally . . . ] external ‘wiring diagram’ with a high information content . . . Organization, then, is functional complexity and carries information. It is non-random by design or by selection, rather than by the a priori necessity of crystallographic ‘order.’ [“The Generation of Complexity in Evolution: A Thermodynamic and Information-Theoretical Discussion,” Journal of Theoretical Biology, 77 (April 1979): p. 353, of pp. 349-65. (Emphases and notes added. Nb: “originally” is added to highlight that for self-replicating systems, the blue print can be built-in. Observe also, the idea roots of the summary terms specified complexity and/or complex specified information (CSI) and functionally specific complex organisation and/or associated information, FSCO/I.)]
Where, we may illustrate a nodes + arcs wiring diagram with an exploded view (forgive my indulging in a pic of a classic fishing reel):
That is, the issue pivots on being able to specify an island of function T containing the observed case E and its neighbours, or the like, in a wider sea of possible but overwhelmingly non-functional configurations [OMEGA], then challenging the atomic and temporal resources of a relevant system — our solar system or the observed cosmos — to find it via blind, needle in haystack search.

In the case of our solar system of some 10^57 atoms, which we may generously give 10^17 s of lifespan and assign actions at the fastest chemical reaction times, ~10^-14 s, we can see that if we were to give each atom a tray of 500 fair H/T coins, and toss and examine the 10^57 trays every 10^-14s, we would blindly sample something like one straw to a cubical haystack 1,000 light years across as a fraction of the 3.27 * 10^500 configurational possibilities for 1,000 bits.
Such a stack would be comparable in thickness to our galaxy at its central bulge.
Consequently, if we were to superpose our haystack on our galactic neighbourhood, and then were to take a blind sample, with all but absolute certainty, we would pick up a straw and nothing else. Far too much haystack vs the “needles” in it. And, the haystack for 1,000 bits would utterly swallow up our observed cosmos, relative to a straw-sized scale for a 10^80 atoms, 10^17 s, once each per 10^-14 s search. Just, to give a picture of the type of challenge we are facing.
(Notice, I am here speaking to the challenge of blind sampling based on a small fraction of a space of possibilities, not a precise probability estimate. All we really need to see is that it is reasonable that such a search would reliably only capture the bulk of the distribution. To do so, we do not actually need odds of 1 in 10^150 for success of such a blind search, 1 in 10^60 or so, the result for a 500-bit threshold, solar system scale search on a back of envelope calculation, are quite good enough. This is also closely related to the statistical mechanical basis for the second law of thermodynamics, in which the bulk cluster of microscopic distributions of matter and energy utterly dominates what we are likely to see, so the system tends to move strongly to and remain in that state-cluster unless otherwise constrained. And that is what gives teeth to Sewell’s note that we may sum up: if something is extremely unlikely to spontaneously happen in an isolated system, it will remain extremely unlikely, save if something is happening . . . such as design . . . that makes it much more likely, when we open up the system.)
Or, as Wikipedia’s article on the Infinite Monkey theorem (which was referred to in an early article in the UD ID Foundations series) put much the same matter, echoing Emile Borel:

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare.
In this context, “almost surely” is a mathematical term with a precise meaning, and the “monkey” is not an actual monkey, but a metaphor for an abstract device that produces an endless random sequence of letters and symbols. One of the earliest instances of the use of the “monkey metaphor” is that of French mathematician Émile Borel in 1913, but the earliest instance may be even earlier. The relevance of the theorem is questionable—the probability of a universe full of monkeys typing a complete work such as Shakespeare’s Hamlet is so tiny that the chance of it occurring during a period of time hundreds of thousands of orders of magnitude longer than the age of the universe is extremely low (but technically not zero) . . . .
Ignoring punctuation, spacing, and capitalization, a monkey typing letters uniformly at random has a chance of one in 26 of correctly typing the first letter of Hamlet. It has a chance of one in 676 (26 × 26) of typing the first two letters. Because the probability shrinks exponentially, at 20 letters it already has only a chance of one in 2620 = 19,928,148,895,209,409,152,340,197,376 (almost 2 × 1028). In the case of the entire text of Hamlet, the probabilities are so vanishingly small they can barely be conceived in human terms. The text of Hamlet contains approximately 130,000 letters.[note 3] Thus there is a probability of one in 3.4 × 10183,946 to get the text right at the first trial. The average number of letters that needs to be typed until the text appears is also 3.4 × 10183,946,[note 4] or including punctuation, 4.4 × 10360,783.[note 5]
Even if every atom in the observable universe were a monkey with a typewriter, typing from the Big Bang until the end of the universe, they would still need a ridiculously longer time – more than three hundred and sixty thousand orders of magnitude longer – to have even a 1 in 10500 chance of success.
The 130,000 letters of Hamlet can be directly compared to a Genome at 7 bits per ASCII character , i.e. 910 k bits, in the same sort of range as a genome for a “reasonable” first cell-based life form. That is, we here see how the FSCO/I issue puts a challenge before any blind chance and mechanical necessity. In effect, such is not a reasonable expectation, as storage of information depends on high contingency [a necessary configuration will store little information], but searching the relevant space of possibilities then is not practically feasible.
The same Wiki article goes on to acknowledge the futility of such searches once we face a sufficiently complex string-length:
One computer program run by Dan Oliver of Scottsdale, Arizona, according to an article in The New Yorker, came up with a result on August 4, 2004: After the group had worked for 42,162,500,000 billion billion monkey-years, one of the “monkeys” typed, “VALENTINE. Cease toIdor:eFLP0FRjWK78aXzVOwm)-‘;8.t” The first 19 letters of this sequence can be found in “The Two Gentlemen of Verona”. Other teams have reproduced 18 characters from “Timon of Athens”, 17 from “Troilus and Cressida”, and 16 from “Richard II”.[24]
A website entitled The Monkey Shakespeare Simulator, launched on July 1, 2003, contained a Java applet that simulates a large population of monkeys typing randomly, with the stated intention of seeing how long it takes the virtual monkeys to produce a complete Shakespearean play from beginning to end. For example, it produced this partial line from Henry IV, Part 2, reporting that it took “2,737,850 million billion billion billion monkey-years” to reach 24 matching characters:
- RUMOUR. Open your ears; 9r"5j5&?OWTY Z0d…
500 bits is about 72 ASCII characters, and the configuration space doubles for each additional bit, we are looking at being able to search a space of 10^50, about a factor of 10^100 short of the CSI/ FSCO/I target thresholds.
Where also, of course, this is a case of an admission against notorious ideological interest on the part of Wikipedia.
But, what about Dawkins’ Weasel?
This was an intelligently targetted search that rewarded non-functional configurations for being an increment closer to the target phrase. That is, it inadvertently illustrated the power of intelligent design; though, it was — largely successfully — rhetorically presented as showing the opposite. (And, on closer inspection, Genetic Algorithm searches and the like turn out to be much the same, injecting a lot of active information that allows overwhelming the search challenge implied in the above. But the foresight that is implied is exactly what we cannot allow, and incremental hill-climbing is plainly WITHIN an island of function, it is not a good model of blindly searching for its shores.)
Another implicit claim is found in the Darwinist tree of life (here, I use a diagram that comes from the Smithsonian, under fair use):
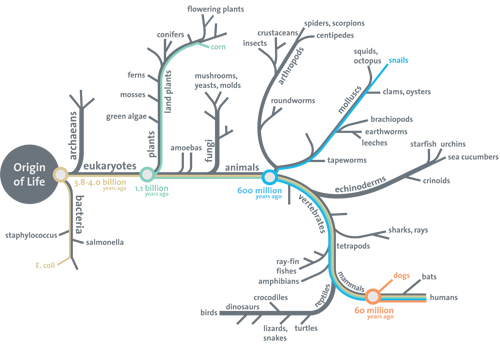
The tree reveals two things, an implicit claim that there is a smoothly incremental path from an original body plan to all others, and the missing root of the tree of life.
For the first, while that may be a requisite for Darwinist-type models to work, there is little or no good empirical evidence to back it up; and it is wise not to leave too many questions a-begging. In fact, it is easy to show that whereas maybe 100 – 1,000 kbits of genomic information may account for a first cell based life form, to get to basic body plans we are looking at 10 – 100+ mn bits each, dozens of times over.
Further to this, there is in fact only one actually observed cause of FSCO/I beyond that 500 – 1,000 bit threshold, design. Design by an intelligence. Which dovetails neatly with the implications of the needle in haystack blind search challenge. And, it meets the requisites of the vera causa test for causally explaining what we do not observe directly in light of causes uniquely known to be capable of causing the like effect.
So, perhaps, we need to listen again to the distinguished, Nobel-equivalent prize holding astrophysicist and lifelong agnostic — so much for “Creationists in cheap tuxedos” — Sir Fred Hoyle:
From 1953 onward, Willy Fowler and I have always been intrigued by the remarkable relation of the 7.65 MeV energy level in the nucleus of 12 C to the 7.12 MeV level in 16 O. If you wanted to produce carbon and oxygen in roughly equal quantities by stellar nucleosynthesis, these are the two levels you would have to fix, and your fixing would have to be just where these levels are actually found to be. Another put-up job? . . . I am inclined to think so. A common sense interpretation of the facts suggests that a super intellect has “monkeyed” with the physics as well as the chemistry and biology, and there are no blind forces worth speaking about in nature. [F. Hoyle, Annual Review of Astronomy and Astrophysics, 20 (1982): 16.]
And again, in his famous Caltech talk:
The big problem in biology, as I see it, is to understand the origin of the information carried by the explicit structures of biomolecules. The issue isn’t so much the rather crude fact that a protein consists of a chain of amino acids linked together in a certain way, but that the explicit ordering of the amino acids endows the chain with remarkable properties, which other orderings wouldn’t give. The case of the enzymes is well known . . . If amino acids were linked at random, there would be a vast number of arrange-ments that would be useless in serving the pur-poses of a living cell. When you consider that a typical enzyme has a chain of perhaps 200 links and that there are 20 possibilities for each link,it’s easy to see that the number of useless arrangements is enormous, more than the number of atoms in all the galaxies visible in the largest telescopes. [–> ~ 10^80] This is for one enzyme, and there are upwards of 2000 of them, mainly serving very different purposes. So how did the situation get to where we find it to be? This is, as I see it, the biological problem – the information problem . . . .
I was constantly plagued by the thought that the number of ways in which even a single enzyme could be wrongly constructed was greater than the number of all the atoms in the universe. So try as I would, I couldn’t convince myself that even the whole universe would be sufficient to find life by random processes – by what are called the blind forces of nature . . . . By far the simplest way to arrive at the correct sequences of amino acids in the enzymes would be by thought, not by random processes . . . .
Now imagine yourself as a superintellect [–> this shows a clear and widely understood concept of intelligence] working through possibilities in polymer chemistry. Would you not be astonished that polymers based on the carbon atom turned out in your calculations to have the remarkable properties of the enzymes and other biomolecules? Would you not be bowled over in surprise to find that a living cell was a feasible construct? Would you not say to yourself, in whatever language supercalculating intellects use: Some supercalculating intellect must have designed the properties of the carbon atom, otherwise the chance of my finding such an atom through the blind forces of nature would be utterly minuscule. Of course you would, and if you were a sensible superintellect you would conclude that the carbon atom is a fix.
Noting also:
I do not believe that any physicist who examined the evidence could fail to draw the inference that the laws of nuclear physics have been deliberately designed with regard to the consequences they produce within stars. [“The Universe: Past and Present Reflections.” Engineering and Science, November, 1981. pp. 8–12]
No wonder, in that same period, the same distinguished scientist went on record on January 12th, 1982, in the Omni Lecture at the Royal Institution, London, entitled “Evolution from Space”:
The difference between an intelligent ordering, whether of words, fruit boxes, amino acids, or the Rubik cube, and merely random shufflings can be fantastically large, even as large as a number that would fill the whole volume of Shakespeare’s plays with its zeros. So if one proceeds directly and straightforwardly in this matter, without being deflected by a fear of incurring the wrath of scientific opinion, one arrives at the conclusion that biomaterials with their amazing measure or order must be the outcome of intelligent design. No other possibility I have been able to think of in pondering this issue over quite a long time seems to me to have anything like as high a possibility of being true. [This appeared in a book of the same title, pp. 27-28. Emphases added.]
Perhaps, the time has come to think again. END
_________________
PS: Let me add an update June 28, by first highlighting the design inference explanatory filter, in the per aspect flowchart form I prefer to use:
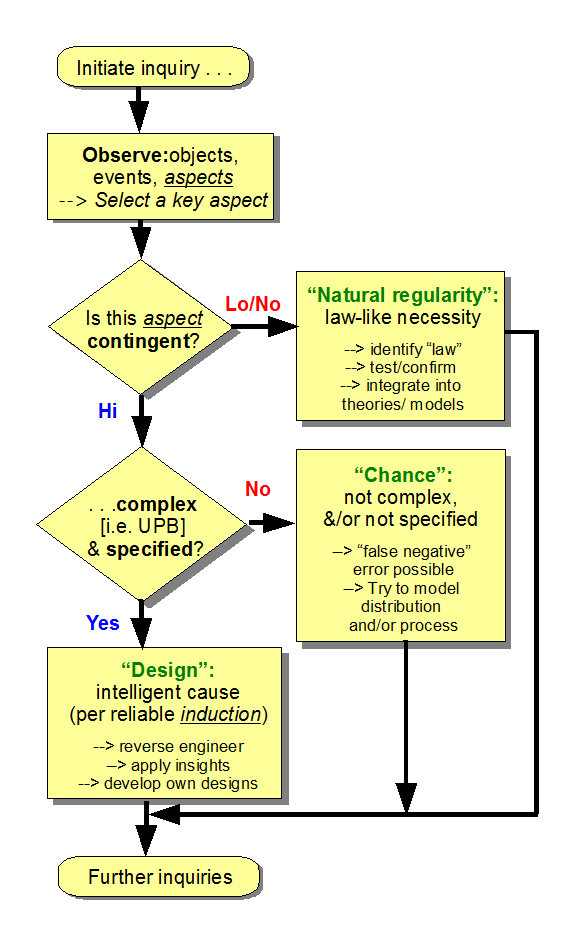 Here, we see that the design inference pivots on seeing a logical/contrastive relationship between three familiar classes of causal factors. For instance, natural regularities tracing to mechanical necessity (e.g. F = m*a, a form of Newton’s Second Law) give rise to low contingency outcomes. That is, reliably, a sufficiently similar initial state will lead to a closely similar outcome.
Here, we see that the design inference pivots on seeing a logical/contrastive relationship between three familiar classes of causal factors. For instance, natural regularities tracing to mechanical necessity (e.g. F = m*a, a form of Newton’s Second Law) give rise to low contingency outcomes. That is, reliably, a sufficiently similar initial state will lead to a closely similar outcome.
By contrast, there are circumstances where outcomes will vary significantly under quite similar initial conditions. For example, take a fair, common die and arrange to drop it repeatedly under very similar initial conditions. It will predictably not consistently land, tumble and settle with any particular face uppermost. Similarly, in a population of apparently similar radioactive atoms, there will be a stochastic pattern of decay that shows a chance based probability distribution tracing to a relevant decay constant. So, we speak of chance, randomness, sampling of populations of possible outcomes and even of probabilities.
But that is not the only form of high contingency outcome.
Design can also give rise to high contingency, e.g. in the production of text.
And, ever since Thaxton et al, 1984, in The Mystery of Life’s Origin, Ch 8, design thinkers have made text string contrasts that illustrate the three typical patterns:
1. [Class 1:] An ordered (periodic) and therefore specified arrangement:
THE END THE END THE END THE END
Example: Nylon, or a crystal . . . .
2. [Class 2:] A complex (aperiodic) unspecified arrangement:
AGDCBFE GBCAFED ACEDFBG
Example: Random polymers (polypeptides).
3. [Class 3:] A complex (aperiodic) specified arrangement:
THIS SEQUENCE OF LETTERS CONTAINS A MESSAGE!
Example: DNA, protein.
Of course, class 3 exhibits functionally specific, complex organisation and associated information, FSCO/I.
As the main post shows, this is an empirically reliable, analytically plausible sign of design. It is also one that in principle can quite easily be overthrown. Show credible cases where cases of FSCO/I beyond a reasonable threshold are observed to be produced by blind chance and/or mechanical necessity.
Absent that, we are epistemically entitled to note that per the vera causa test, it is reliably seen that design causes FSCO/I. So, it is a reliable sign of design, even as deer-tracks are reliable signs of deer:

Consequently, while it is in-principle possible for chance to toss up any outcome from a configuration space, we must reckon with available search resources and the plausibility that feasible blind samples would be reasonably expected to catch needles in the haystack.
As a threshold, we can infer for solar system scale resources that, using:
Chi_500 = Ip*S – 500, bits beyond the solar system threshold,
we can be safely confident that if Chi_500 is at least 1, the FSCO/I observed is not a plausible product of blind chance and/or mechanical necessity. Where, Ip is a relevant information-content metric in bits, and S is a dummy variable that defaults to zero, save in cases of positive reason to accept that observed patterns are relevantly specific, coming from a zone T in the space of possibilities. If we have such reason, S switches to 1.
That is, it is default that first, something is minimally informational. the result of mechanical necessity, which would show as a low Ip value. Next, it is default that chance accounts for high contingency so that while there may be a high information-carrying capacity, the configurations observed do not come from T-zones.
Only when something is specific and highly informational (especially functionally specific) will Ip*S rise beyond the confident detection threshold that puts Chi_500 to at least 1.
And, if one wishes for a threshold relevant to the observed cosmos as scope of search resources, we can use 1,000 bits as threshold.
That is, the eqn summarises what the flowchart does.
And, the pivotal test is to find cases where the filter would vote designed, but we actually observe blind chance and mechanical necessity as credible cause. Actually observe . . . the remote past of origins or the like is not actually observed. We only observe traces which are often interpreted in certain ways.
But, the vera causa test does require that before using cause-factor X in explaining traces from the unobserved past, P, we should first verify in the present through observation that X can and does credibly produce materially similar effects, P’.
If this test is consistently applied, it will be evident that many features of the observed cosmos, especially the world of cell based life forms, exhibit FSCO/I in copious quantities and are best understood as designed.
IF . . .