Hasn’t Quantum Theory proved that the law of non-contradiction that ID thinkers use is outdated?
Weak Argument: At its foundation ID is based on a logical construct that posits that for any proposition A, A cannot be true and false at the same time and in the same formal relation. Modern quantum mechanics has proven this logical construct – the so-called “law of non-contradiction” — is outdated and does not always holds true.
Now, in the in-a-nutshell form of the answer to this question, we showed how:
. . . the heart of the scientific method inescapably and deeply embeds the classic laws of thought. You cannot do science, including Quantum Theory science, without basing your work on the laws of thought. So, it is self-refuting and absurd to suggest that Quantum Theory results can or do undermine these laws of thought.
But, unfortunately, that blunder is exactly what is now all too commonly seen; too often, from physicists who should know better, but don’t. A typical example of the problem is found in physicist Dr Larry Krauss’ opening remarks during his debate with philosopher Dr William Lane Craig:
“The interesting thing about the universe is it’s not logical. At least it’s not classically logical….It’s [science] taught us that the universe is the way it is whether we like it or not….The point is if we continue to rely on our understanding of the universe on…classical logic…then we’d still be living in a world where heavier objects, we think, fall faster than light objects…instead of doing the experiment to check it out. We can’t rely on what we think to be sensible; we have to rely on what the universe tells us is sensible….The universe just simply isn’t sensible.” [Transcribed, Randy Everist. Debate videos here.]
Obviously, and sadly, Dr Krauss is unaware that:
If a scientific theory,T is consistent with and predicts observations O, but we see the denial of O, i.e. NOT-O, O is first seen as distinct and recognisably different from NOT-O [LOI]. We can also see that O and NOT-O cannot both be so in the same sense and circumstances [LNC], and once O is distinct they would see O or NOT-O, not both or something else [LEM]. Going further, when scientists scratch out their equations and derivations on their proverbial chalk boards, they are using distinct symbols, and are reasoning step by step on these same three laws.
An online exchange here, shows the sort of claims Krauss was getting at:
[Anonymous Physicist:] Do you know anything about quantum mechanics, for example? About the fact that there can be linear superpositions of physical states? . . . . we can have a state of physical reality where an electron has spin “up” and spin “down” simultaneously . . . . It is equivalent to having a person being alive and dead, simultaneously. Presumably you would claim that a person cannot be both alive and dead simultaneously. But quantum mechanics proves otherwise *with the following caveat*. . . . Macroscopic states, due to something called “decoherence”, generally assume classical behaviors . . . . I cannot accept the “law of noncontradiction” because I know of instances where it does not apply . . . . there is a problem with classical notions of contradiction when one goes to the quantum level — the way the universe works . . .
To see where this argument goes off the rails, let’s remind ourselves of UD contributor StephenB’s key principle: Scientists do not use observed evidence to evaluate the principles of logic; they use the principles of logic to evaluate such evidence. It is only by following this approach that the researcher can uncover counterintuitive observed facts about nature and develop groundbreaking models, laws or theories for explaining them. Only through rationality can we discover surprises and anomalies because only rationality can tell us what is odd.
We can see this from the way that the very same quantum mechanics was put together; not least because we may otherwise lose our way in the thicket of quantum weirdness.
Now, proverbially, the theoretical physicists of a century ago scratched out their analyses on chalk boards, as we can here see from Einstein’s office as he left it:
(Source: Life magazine, fair use)
To work on those chalk boards, the physicists used specific chalk scratch-marks that functioned as symbols connected together in rather definite ways, e.g. h for the now famous Planck’s constant 6.626 *10^ -34 Js. So, for instance when Einstein explained the photoelectric effect and thus set quantum theory on its feet once and for all (it had been viewed as rather dubious till that time) — winning a Nobel Prize along the way – he deduced something like:
KE_max = h*f – w
Each of these symbols is quite definite and symbolises something specific. The mathematical-logical relationships between them are just as definite, too.
First, the photon – this is where it got its name – has a definite energy h*f, and that energy is tied to the frequency of the light being shone on a metal surface, potentially triggering emission of electrons. Where also, for electrons to be emitted from the metal’s surface and fly off, the energy of the photon must be enough to overcome the work function, w. The remainder ends up as electron energy of motion, KE (up to a definite maximum value). Also, below a certain frequency, even with quite bright light, essentially no electrons are emitted. Above it, even with very weak light, electrons are emitted; there is a frequency threshold. Lastly, the work function is a measure of the relevant potential barrier for the metal surface.
That is, we are here seeing how, even in quantum mechanics, our thinking and correlation of that thinking with reality as observed pivot on the recognition of distinct identity and on not confusing things with their opposites, as a crucial first step of reasoned scientific and general thought.
So, first ,we recognise the world around us, with all sorts of things in it; as a common point of our experience:
I: { . . . * * * . . . }
(I experience/observe a world full of different things, of various sorts.)
Next, we observe something specific in it, whether Einstein’s scratch-marks on a chalk board or a red ball on a table or a stream of photo-emitted electrons when light hits a metal surface in a vacuum, or whatever:
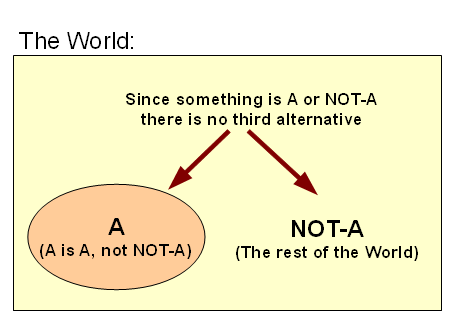
I:A –> {(A) | NOT-A}
(I observe A and infer A distinct from not-A, the rest of the world.)
But is this all in the head, a mental world of phenomena that is on one side of an unbridgeable gulf to the world of things as they are in themselves?
No, that is an error, for as F H Bradley noted (and as W L Craig cited):
“The man who is ready to prove that metaphysical knowledge is impossible has . . . himself . . . perhaps unknowingly, entered the arena [of metaphysics] . . . . To say that reality is such that our knowledge cannot reach it, is to claim to know reality.” [Appearance and Reality, 2nd Edn. (Clarendon Press, 1930), p.1]
If logic was not linked to the real world, we could not understand or think rationally about our everyday experiences or scientific experiments alike.
To be sure, we could advance VALID arguments (those that play by the rules of the little game called logic . . . ). However, we could not, under those circumstances, present SOUND arguments – those that are not only valid but stand on true premises and lead to true conclusions by helping us make correct inferences as to what follows from such premises. Where truth “tells it like it is,” about reality.
So, if logic cannot connect to reality through true premises, there would be no way that we could make our arguments and conclusions connect accurately to reality. Which of course is a principal aim of scientific reasoning: to accurately describe and explain the world, based on careful observations.
We may indeed err in our perceptions and thoughts about reality, but that is itself to already know something about extra-mental reality beyond reasonable doubt: we are error-prone creatures.
So, knowledge is not hopelessly subjective.
Indeed, Josiah Royce takes this principle and uses it to ground truth and knowledge: “error exists” is undeniably true as to try to deny it is at once to confirm instead. So, truth exists – as that which says of what is that it is, and of what is not, that it is not (Aristotle, Metaphysics, 1011b) — and credibly warranted truth exists. Therefore, knowledge exists.
Let’s get back on track:
(a) we have seen how we routinely recognise distinct realities, e.g. A, that we can mark out as separate from the rest of the world, NOT-A. From this, we then
(b) see that A is itself, and A is not to be confused with or equated to what is not itself, NOT-A. Also,
(c) given the recognised distinction{(A) | NOT-A}, there is no third option to A and NOT-A that bridges the borderline or branches off from it or is embedded in it. That is,
(d) the “middle” is excluded once we have an act of distinct recognition of a specific, A.
Just so, if at any time we recognise ANY distinct identity, all of that follows, quite naturally. It is not an alien and arbitrary “axiom” unconnected to experienced reality that sets up rules for an idle game we call “logic.” Instead, we can see a common sense form of the classical three main laws of thought, that come about once we have in mind a given thing A, e.g. a bright red ball lying on a table:
(Source: TKI, fair, non-commercial use permission granted)
[a] A thing, A, is what it is (the law of identity);
[b] A thing, A, cannot at once be and not-be (the law of non-contradiction);
[c] A thing, A, is or it is not, but not both or neither (the law of the excluded middle).
In short, reality imposes the principle and experience that we may accurately recognise real things. So also we can see that the same thing cannot be A and NOT-A in the same sense and circumstances, and that something is going to be either A or NOT-A, but not both and not neither.
That bright red ball on the table again.
And, those quantum theory equation scratched on the chalk board again.
Not to mention that strange threshold effect where dim light above a certain frequency triggers photoelectrons, but bright light below the thresholds does not. And the like.
Further to all this, plainly, we can at least sometimes accurately describe and state what we see or think, saying what is or is not. Such assertions of what is or is not are called propositions, like: Socrates is a man. Which could also be expressed as There Exists s: sele M, where s stands for the claim, that there exists a certain Socrates and the colon ( : ) means “such that,” where also s ele M, says that s is an individual member of the set M for Man. (The usual symbols for existential quantifier and being a member of can be inserted if you know them.) We have a set M., with s in it:
M: { . . . s, . . . }
So, then, we have propositions as potentially true claims, the meaning in the statements we make when we say that something is true or false.
In dealing with such propositions, the key law, non contradiction, says that we cannot have A being both true and false in the same sense under the same circumstances:
NOT (A and NOT-A)
NOT (Socrates is a man and Socrates is not a man)
. . . and, the three classic laws of thought are now:
(a) A is A (symbolically, [A => A] = 1),
(b) A will not be the same as NOT-A ( [A AND NOT-A] = 0); and
(c) there is no third option to being A or NOT-A ( [A OR NOT-A] = 1).
But, a whole raft of further debates can be triggered. For instance, what of “this sentence is false” and “the Barber shaves those men of the village who who do not shave themselves, so who shaves him?” Or “Cretans are liars” so do we believe this when spoken by a Cretan?
These and many other similar pathological cases just show us how easy it is to tangle ourselves up in our words, seeming to assert what is or is not, but only managing to hopelessly contradict ourselves.
A self-referential argument, sentence or claim may well contradict itself and is thus false. The Barber paradox shows that not all groups that we may describe in seemingly plausible words are valid sets; hence, why more sophisticated forms of set theory were created. Also, yes perhaps Cretans are liars (like most of us), but on Kant’s Categorical Imperative, we can be sure they are not lying every time they open their mouths or society would break down, making lying pointless: lying only works when it is relatively rare. Even, for Cretans.
Another favourite objection is the case of vague memberships, like how do we define a bald man, or the shades of grey between white and black. The easiest way to think of this sort of thing is to use a control systems example where Fuzzy Set Membership is defined and used to drive crisp control action.
For instance, we may look at a system where control action must respond to the ambient temperature [say, the response of an air conditioner to its load on a cold, warm or hot day] where three ideal points for cold, warm and hot have been defined. It is often useful to then define that at any given temperature the controller should trigger a weighted average of the required control actions for cold, warm and hot, e.g. a certain temperature can be viewed as 30% hot, 60% warm and 10% cold. But that certain temperature is a definite item, and we are giving it a functional weighting relative to certain ideal ranges to decide just what equally specific control action should be carried out based on a weighted superposition of the three cases.
Similarly, we can regard shades of grey as superpositions of white and black. But that does not mean that white and black have lost their meaning, just that they can be blended to give particular greys, say:
70% W + 30% B –> 70/30 G
Further to this, computer screens define colours by a similar process of weighted mixing of red, green and blue.
We can see that superposition of parent inputs yields a child outcome but has not removed the distinction between the parents. Just because greys exist does not mean that black and white are now meaningless or to be seen as more or less the same.
Standing waves in physics, like those on a string, are a classic case of such superposition, as the fixed ends of the string force these to be nodes, best thought of as what happens when waves moving to the left and the right superpose. That in turn means that there are natural vibration frequencies of a stretched string, which will be quantised – these modes come at distinct, separate frequencies.
It should turn out to be no surprise, then, to see that how the quantization of energy levels emerges in a quantum system is that when a microscopic particle is confined in a “box” or a potential well, it has similar boundary conditions that create in effect standing waves. That’s where the quantization typically comes from.
Going further, when we fire such matter-wave micro-particles (e.g. electrons) at a double slit, the waves superpose and interfere rather like water ripples in a ripple tank and that is where we get the strange effect that say electrons will hit a detector screen in front of a double slit in an interference pattern. It looks rather like:
. . . | | | | | . . .
This happens, providing, we do not disturb the set-up by trying to observe the “actual path.” If we do so, we have triggered collapse of the wave function and will see a “particle pattern” — two bands — instead:
| |
This of course tells us that matter on the small scale has both wave and particle properties, which we may see in one setup or another. But if we go looking for particles, the act of intervening to detect such triggers a “collapse” of the waves. Just what these waves are has been of course disputed since the 1920’s and we obviously are not going to resolve it in this note. (In short, the shut up and calculate school of thought has a point: a scientific theory or model is a map, not the actual territory.)
Something else is looming through the mists of this weird and wonderful quantum world: we are looking at very definite things, and are making very definite calculations and tests where successful prediction counts for a lot. As in, we are using the principles of identity and non-contradiction and the distinctness of being one thing or not that thing, all along the way.
So, first and foremost, the reply to the main objection above is that not even physicists can get away with sawing off the branch on which they are sitting. That is:
Quantum physicists, just as the rest of us, are utterly and inescapably dependent on the basic laws of logical reasoning when they carry out their quantum analyses and experiments. So, to reject such logic on the strength of observed results “contradicting” the predictions of an older theory in physics, e.g. showing us that a single photon or electron seems to interfere with itself in a double slit experiment (or that it “knows” when it is being watched, before or after the slits), or that there are superposed states, is to implicitly use and take for granted the very logic one wishes to reject. For we are reasoning thusly: If a theory T were true, the observations O would follow. But, NOT-O, so NOT-T. In short, all along, we are implicitly assuming and using the law of non-contradiction, build into the heart of the scientific method. To then turn around and assert that the method now shows that the logic that underlies it does not work, is confusion. Yes, at small scale matter shows wave-like properties, which leads to superposition, interference etc. and all sorts of weirdness. That just means we have to reckon with that, not that the underlying logic we have but little choice to use, has broken down.
Again: it makes no sense to saw off the branch on which one sits.
Yes, quantum results are strange indeed, what with particles dissolving into a strange hybrid, the wavicle, that tends to penetrate barriers, and manifests waves that interfere, superposes, etc etc. But we again see one of the key problems; since we are analysing quantum realities based on familiar objects – “particles,” and “waves,” we are making models or maps, we do not have a direct, God-like access to quantum reality. Indeed, the uncertainty principles that we cannot refine position and momentum or energy and time observations below a certain limit, tell us that.
The map is not the territory, and we should not be surprised that the quantum world of the very small is not like our expectations.
But, in all of this strangeness, when we appeal to observational evidence as a test of the accuracy of our theories, laws and models, we are implicitly relying on the three key laws of logic. The same holds when we carry out the analyses that give us scientific laws, models and theories by scratching, interpreting and manipulating symbols on the proverbial chalk boards, or their modern computer replacements.
To then try to use this process to claim that the root principle we are relying on to develop what we are doing, and to test the results against observations is now overturned, because . . . the predictions contradict our observations . . . is to saw off the branch on which we are sitting.
Science, like any other rational activity, implicitly relies on these laws of thought, and can neither prove nor disprove them. The only reasonable basis we can hold them on is that they are self-evident and undeniable, i.e. to try to deny or dismiss them directly lands us in patent absurdities. Such as we just saw.
Other things, we may test. These, we must hold trustworthy, if we are to test at all.
We can go on, summarising a cluster of six key first principles of right reason that we all implicitly depend on in our reasoning, and that when one objects, sooner rather than later s/he will be sawing away at the branch on which s/he sits:
Consider the world as we experience and observe it, with various things in it:
{ . . . * * * . . . }
Identify some definite A in it:
{ . . . (A) | NOT-A (the rest of the world) . . . }
Notice, the point of the “pipe” character, |, is to mark the boundary of distinction, i.e. we have A, and we have everything else, which is NOT-A.
Now, let us analyse, stating six First Principles of Right Reason:
[1] A thing, A, is what it is (the Law of Identity);
[2] A thing, A, cannot at once be and not-be (the Law of Non-Contradiction).
–> It is worth clipping Wiki’s cites from Aristotle in Metaphysics, to show this in different forms:
1. ontological*: “It is impossible that the same thing belong and not belong to the same thing at the same time and in the same respect.” (1005b19-20)
[*NB: Ontology, per Am HD etc, is “The branch of metaphysics that deals with the nature of being,” and the ontological form of the LNC is talking about that which really exists or may really exist, once we have some definite thing A in the world, e.g. Socrates as a Man, or men as rational animals.]
2. psychological: “No one can believe that the same thing can (at the same time) be and not be.” (1005b23-24)
3. logical: “The most certain of all basic principles is that contradictory propositions are not true simultaneously.” (1011b13-14)
[3] A thing, A, is or it is not, but not both or neither (the Law of the Excluded Middle).
[4] “to say that what is is, and what is not is not, is true.” (Aristotle, Basic Definition of Truth, i.e. “telling it like it is.”)
[5] “Of everything that is, it can be found why it is.” (Principle of Sufficient Reason, per Schopenhauer.)
[6] If something has a beginning or may cease from being — i.e. it is contingent — it has a cause.* (Principle of Causality, a direct corollary of principle [5]. Cf. the discussion at UD here. Principles 5 and 6 are especially relevant to science and to the debates over design theory. Typically, issues over principles 1 – 3 emerge in debates that start over 6 and 5, with the added issue that nothing properly means non-being, “what rocks dream of,” as Aristotle put it, for rocks do not dream! Design thinkers are firmly committed to the view that from such non-being — no matter in any form, and similarly no energy, no space, no time, no fields, no mind etc., nothing can or does come to be. Non-being has no causal power, in short.)
_________
*F/N: Principles 5 & 6 point to the possibility of necessary, non-contingent beings, e.g. the truth in 2 + 3 = 5 did not have a beginning, cannot come to an end, and is not the product of a cause, it is an eternal reality. In this context, too, we must give a basic definition of nothing: non-being, or as Aristotle put it, “what rocks dream of” – as, rocks plainly don’t have dreams. The most significant candidate necessary being is an eternal Mind. Indeed, down this road lies a path that has led many to to infer and argue for the existence of God as architect, designer and maker of the cosmos. (Cf. Plato’s early argument along such lines, here.)
(If you doubt that these six first principles of right reason are indeed self evident first principles, try the “saw off the branch . . .” test for yourself: see if you are indeed forced to rely on what you are trying to dismiss when you go about scientific and other reasoning. If, in order to think soberly about serious things, you have to use a principle of thought, then to swivel around and object to it when a design thinker uses it is self-referentially absurd and selectively hyperskeptical. It is self-defeating or self-refuting and indeed, patently irrational. You may also find the posts and discussions at UD here and here helpful.)
-END-