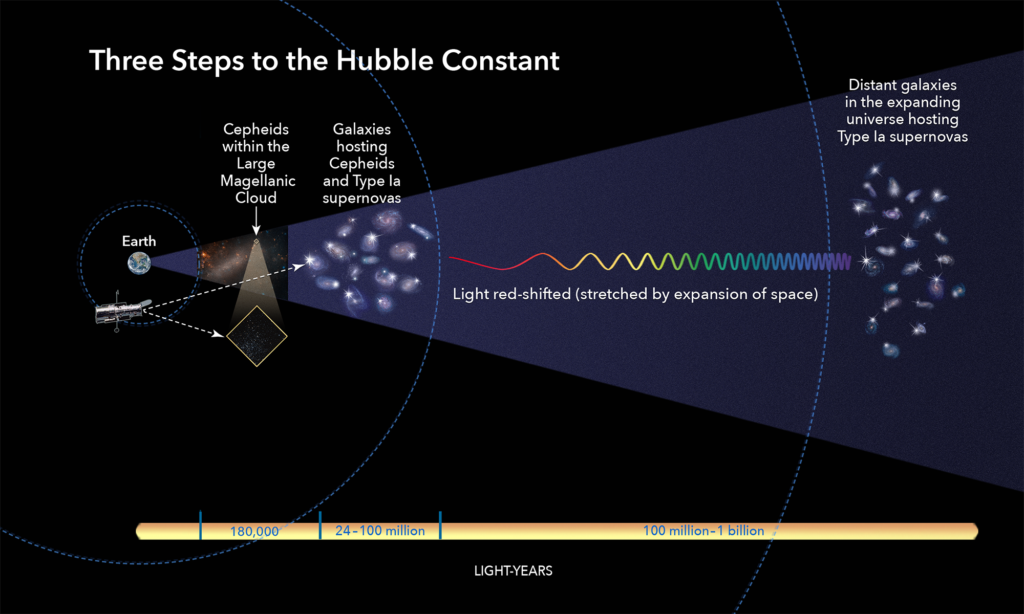
The three basic steps astronomers use to calculate how fast the universe expands over time, a value called the Hubble constant. /NASA, ESA, and A. Feild (STScI)
Recently, we heard that new Hubble measurements show that the universe is expanding much faster than expected:
New measurements from NASA’s Hubble Space Telescope confirm that the Universe is expanding about 9% faster than expected based on its trajectory seen shortly after the big bang, astronomers say.
The new measurements, accepted for publication in Astrophysical Journal, reduce the chances that the disparity is an accident from 1 in 3,000 to only 1 in 100,000 and suggest that new physics may be needed to better understand the cosmos.
“This mismatch has been growing and has now reached a point that is really impossible to dismiss as a fluke. This is not what we expected,” says Adam Riess, Bloomberg Distinguished Professor of Physics and Astronomy at The Johns Hopkins University, Nobel Laureate and the project’s leader. Chanapa Tantibanchachai, “New Hubble Measurements Confirm Universe Is Outpacing All Expectations of its Expansion Rate” at Johns Hopkins University
We asked Rob Sheldon, our physics color commentator, to help us understand what that implies:
—
The news isn’t exactly new, we have been hearing this for several years now. The essential problem is not the expansion of the universe (that goes back to the 1920’s and the Hubble constant), nor is it acceleration of the universe (that is the dark energy hypothesis, and the 2011 Nobel prize was awarded to Riess, Perlmutter & Schmidt for supposedly demonstrating this with supernovae).
Rather the hullabaloo is that two different methods for measuring Hubble’s constant (H0) are disagreeing. The measurement of Hubble’s constant has been an ongoing task since 1927, and one of my professors in grad school, Virginia Trimble, has written a series of papers on the history of that measurement: Here. , here, and here.
In units of km/s/parsec, H0 has been as high as 625 (Lemaitre) and as low as 33 (Trimble). Over the years, different methods have converged on a number around either 68 or 74. At first, the error bars were large and no one thought too much of the discrepancy, but in recent years the error bars have shrunk to less than 2, and shown no sign of converging. That is to say, there’s less than one chance in million that the two numbers will magically agree in the future.
What does this mean?
Well the two methods differ in that one is “direct” and the other “indirect”. Clearly one or both of them is making a mistake. Since it is hard to find (and people have looked) a reason why the direct method is failing, the feeling is that the indirect method must have a mistake in its model.
To explain further, here is a long description of the two approaches.
Starting with the direct method, we measure the difference to neighboring galaxies, measure how fast the galaxy is moving away using the red shift, and plot up thousands of galaxies to see how their distance from us is correlated to their speed away from us. A best fit line is plotted up, and we get Hubble Constant = 74 km/s/parsec. The red shift measurement is good to 4 or 5 decimal places, but the distance is a bit tricky, which is described next.
Nearby stars we can measure by parallax (like using two eyes to thread a needle), but for more distant stars we need to use Cepheid variables. Nearby galaxies have distinguishable Cepheids, but distant galaxies are just a blur. So we construct a “distance ladder”, use parallax on nearby Cepheids to calibrate, then use Cepheids in nearby galaxies to calibrate, then use calibrated galaxies (Fisher-Tully) to measure truly distant galaxies, and finally use supernovae in calibrated galaxies to measure truly distant supernovae. This chain gives us distances which we can then plot the red-shift to get the velocity. The recent measurement discussed in this article was done by Adam Riess on Cepheids in nearby galaxies to recalibrate and check the first “step” on the ladder, whose errors propagate up the ladder, so we need to know it precisely.
The 2nd method of measuring Hubble’s constant, is to find the “temperature” of the Cosmic Microwave Background Radiation (CMBR). One prediction of Lemaitre’s “Big Bang” was that we should see the afterglow of the explosion today, but greatly cooled down by the expansion of the universe. In 1978 Penzias and Wilson got the Nobel prize for having discovered this afterglow in the microwave spectrum while setting up a satellite communication systems to look at the sky. As you all know from your stove heating elements, a cold stove is black, a hot one is cherry red, and should you have a welder’s torch, a really, really hot stove element is blue-white. The color comes from the shape of the “blackbody spectrum” or the light emitted from hot objects. (It’s called blackbody because the color doesn’t come from paint.)
So by measuring the temperature of the CMBR with 9 different microwave channels the Planck satellite could fit a really good curve through the data and get the temperature to 4 or 5 decimal places. This tells us the temperature of the universe now.
Right after the Big Bang, when was really, really hot, the electrons both emitted light and absorbed it, but on the whole, absorbed it. Electrons made the universe opaque, so the universe was black. As it cooled a bit, the electrons found protons, made hydrogen, and the density of electrons dropped, making the universe transparent, and allowing the light to escape. This is known as “decoupling”, and the light that escaped was thermal, blackbody radiation emitted from “cherry red hydrogen” or plasma.
So we have two temperatures we know, plasma and CMBR, and we can calculate how much we have to “stretch” or expand the universe to make the short-wavelength plasma light look like the long-wavelength microwaves we see today. That gives us an expansion factor. In order to get a Hubble constant, we just need to know the time between those two events. And for that we need a model.
The model of choice is called “The Big Bang Nucleosynthesis” model, one of the first computer versions being a FORTRAN code that Hoyle developed in 1967. There’s a lot of things one could say about it, but like Darwinian evolution, the one thing you cannot say is that it is wrong. Many refinements have been added over the years, but the essential 1-dimensional, isotropic, homogeneous, with no magnetic field, version is unassailable, (despite the fact that modern computers can do 3-D, anisotropic, heterogenous magnetized versions.)
Using this model, the Planck team has reduced their temperature data to fit many of the variables in the model, calling their output “precision cosmology”.
The Wikipedia article has a table of 17 model parameters with 4, 5, and sometimes 6 digit accuracy. Well, one of those numbers is the Hubble constant= 67.31 +/- 0.96, which is some 6 error bars (or “six sigma”) from the Hubble Constant =74 of the direct method. Recall that in astrophysics, 5-sigma is the gold-standard. So we’re talking a serious discrepancy.
Then the hand-wringing is that the model might be wrong, and all those 17 precise cosmological parameters might be wrong as well. This is not just embarrassing to the team. A decade or two of cosmology papers have used these numbers as well.
By the way, I’m working on my non-standard model using large magnetic fields in the BBN to generate a very different equilibrium. Preliminary results with some kluged reaction rates were promising, showing that we might be able to explain not just this expansion problem (magnetic fields can seriously distort the universe expansion rate), but also the Li-7 and deuterium abundance problems, dark matter, and horizon problems. Finding collaborators turned out to be the highest hurdle yet to overcome.
—
Sounds interesting. Maybe he needs a Kickstarter fund to support graduate students who sign on to the project. 🙂
![The Long Ascent: Genesis 1â 11 in Science & Myth, Volume 1 by [Sheldon, Robert]](https://images-na.ssl-images-amazon.com/images/I/51G-veeEcdL.jpg)
Rob Sheldon is author of Genesis: The Long Ascent
See also: Is space really the final illusion? Rob Sheldon comments
and
Quadrillion possible ways to rescue string theory. Rob Sheldon comments.
Follow UD News at Twitter!