To support discussion at the ongoing design inference thread, I briefly clip my briefing note, on the Trevors-Abel FSC concept, a way to visualise CSI:
________________
>> It is worth pausing to jump several decades ahead in time, and introduce and briefly comment on an illustrative figure by Trevors and Abel, Fig 4 from their recent [peer-reviewed] 2005 paper on “Three subsets of sequence complexity and their relevance to biopolymeric information”:
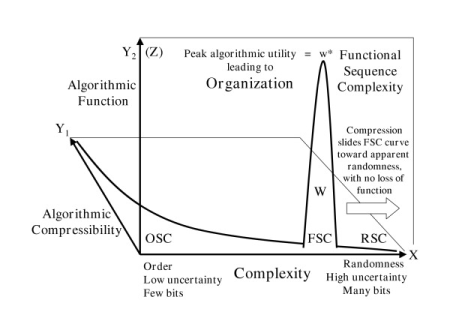
Fig A3.1: Contrasting different types of sequences and their characteristics [used under the US NIH’s Open Access permission]
TA’s description of their Fig 4: Superimposition of Functional Sequence Complexity onto Figure 2 [i.e. from their paper]. The Y1 axis plane plots the decreasing degree of algorithmic compressibility as complexity increases from order towards randomness. The Y2 (Z) axis plane shows where along the same complexity (more …)
Here we may observe that sequences that exhibit order are quite distinct from those that exhibit either random sequence complexity or complex functional organisation. We may observe that complexity is maximised and algorithmic compressibility [ability to be simply and briefly described, in effect] is minimised in a long random sequence [cf TBO’s Class 2 supra]. By contrast, a long but orderly sequence [Class 1] is of high compressibility but low complexity. A long, functionally specified, organised, complex sequence [Class 3] is as a rule not quite as “complex” — per metrics of complexity — as a long random sequence; as it would have in it the redundancies and periodicities that are part and parcel of effective communication. However, by contrast with both order and randomness, it exhibits high functionality; which is of course observable (and so can in principle be associated with a count of the number of ways that components may be configured compatible with that functionality, as opposed to the usually far higher number of possible arrangements in total; cf the microjets case supra). [NB: while of course these ideas are developed relative to linear sequences, they extend to higher dimensionalities as well, and can be generalised in thinking about order, randomness and organised, functional complexity.] . . . >>
____________________
I hope this helps our discussions. END