I dedicate this post to our Denyse O’Leary (UD News desk), who suggested me to deal a bit with this topic.
—
A “whole” (or “all” or “total”) can be a “true whole” or a “false whole”. A “true whole” (or “unit”) is anterior and independent from the consideration of parts, is not obtained from their sum, it doesn’t presuppose them. A “false whole” (or “set”) is the mere sum of parts, is logically posterior to them, and is a fictitious “one” only because we consider it so. While a simple set is artificially composed bottom-up by its parts, a real unit overarches top-down any part.
The above distinction is strictly related to the difference between analysis and synthesis, and the related kinds of knowledge. While analysis is to look at things and data from bottom, by considering any item individually, synthesis is a top vision and global understanding of a true whole. In short, analysis is to see multiplicity in a thing, synthesis is to see its organic unity. Unity is related to the very principle of a thing, and in fact, as A.K.Coomaraswamy said, “the principle of a thing is neither in one of its parts nor in the sum of its parts, but where all its parts are a unity without composition.” Therefore any science entirely and uniquely based on analysis will never reach the ultimate meanings or principles of things:
“Differently from the common opinion, according to which analysis is somehow preparatory to synthesis and leads to it, so that one should always begin with analysis, also when one doesn’t want to stop at it, the truth is one never can effectively reach synthesis by starting from analysis; any synthesis, in the real sense of this term, is something immediate and direct, which is not preceded by any analysis and is fully independent from it, like the mathematical integration is an operation done in a single shot, and that doesn’t presuppose at all the consideration of elements amenable to those of an arithmetic sum; and, as this arithmetic sum cannot provide the means to reach and exhaust the indefinite, so there exist, in all domains, things that resist, for their very nature, to any analysis and whose knowledge is possible only by means of synthesis.” (R. Guénon, “Les Principes du Calcul Infinitesimal”, chap. 21, [my translation from French]).
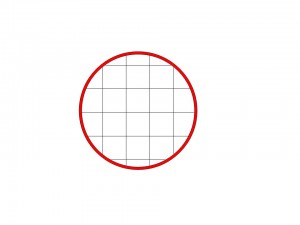
Let’s consider then a mathematical analogy, taken indeed from infinitesimal calculus, which can help to clear the issue (see the picture).
Consider a circle and, inside it, a set of evenly-spaced orthogonal lines describing squares with equal side. If you sum the area of all squares you obtain an imprecise value of the circle’s area. If you thicken the orthogonal lines by decreasing the square’s side and sum their areas you get a better measure. You can iterate this analytic process ad libitum (obtaining always better approximations) but you will never get the exact circle’s area, because the circle is something qualitatively different from squares or any sum of squares or polygons. Circle and square are different archetypes, and the synthetic understanding of the former cannot in principle be reduced to any analysis of the latter. In particular, the exact circle’s area is obtainable only by means of a synthetic operation: the operation that in infinitesimal calculus is called “integration”. This mathematical integration is able to suddenly catch the limit of the succession of all square sums, a limit that is unreachable in the endless analytic process of “squaring”. Just in an example like this one can appreciate how synthesis is different and more powerful than analysis.
As Guénon says, the integration of calculus is only an example / symbol, in the quantitative field of math, of other synthetic operations applicable on higher qualitative fields.
As another application, we can say that analysis vs. synthesis has something to do with the ID / evo debate. Example, when scientists try to reverse-engineer a living being with the mindset and methods of scientism, they are necessarily applying analytic processes, which always will miss the more important aspects of the living beings. Differently, the Designer of the living beings, to design them, used a synthetic knowledge. For this reason any living being entails a organizational principle of organic unity, thanks to which any conception of the being as a simple bottom-up puzzle of plug-in parts or devices is unavoidably reductionistic and simplistic. In short, in principle, in any field, intelligent design is related to synthesis while any non-teleological perspective is related to analysis. What applies to the microcosmos also does to the macrocosmos. So any analytic materialist conception of the cosmos as a bottom-up “evolution of intelligence from matter” is unable to grasp the integrated unity of this grand design.
Last but not least, in ontology, only a synthetic operation of our intellectual intuition can help us to conceive the supreme Being. The Being is not whatever sum of beings or existent things, like a circle is not a sum of squares. The Being transcends any existence, likewise the circle transcends any succession of inscribed polygons. As a consequence, pantheism or other similar modern ideas, which considers God as the analytic sum or set of all existent things, is an entirely absurd conception, since God is the metaphysical supreme Synthesis, or, in a math-symbolic sense, — as mathematician Sara Voss wrote in her “What Number Is God?” — the infinite-dimensional supreme Integral.