The Fourier series is a powerful technique that can be used to break down any repeating waveform into sinusoidal components, based on integer number harmonics of a fundamental frequency:
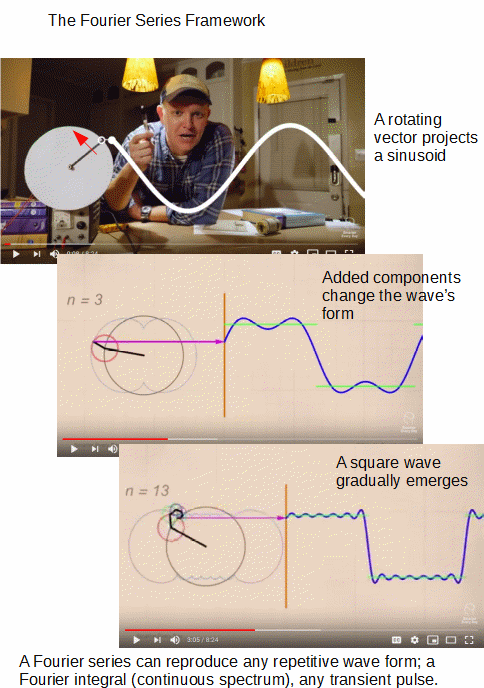
Video:
This is already amazing, that by summing up harmonically related sinusoids (with suitable amplitudes and lagging) we can analyse any repeating waveform as a sum of components. This then extends to any non-repeating pulse, once we go to an integral, which brings in the idea of a continuous spectrum where some wave “energy” is found at every particular frequency in a band.
However, something subtler lurks: As the illustration based on clips from the video shows, a sinusoid can be seen as the projection of a rotating vector (= a phasor). Thus, what the Fourier series is doing is that it is adding up a set of harmonically related rotating vectors instant by instant, yielding the overall result of the periodic waveform (here, a square wave). And indeed, we can get the rotation by adding up two perpendicular oscillating vectors, one on oX, the other on oY. This then gives us two summed harmonic motions, which allows us to bring in the forces and inertia at work. (Where, yes, we can then go on to elliptical, parabolic, hyperbolic and even linear motion.)
Rotating vectors should ring a few bells for those who have been following our discussion recently.
Yes, we can start with the von Neumann construction of the natural counting numbers, N:
{} –> 0
{0} –> 1
{0,1} –> 2, etc
And from that define integers (Z), then rational numbers (Q) then reals, R, eventually the surreals:
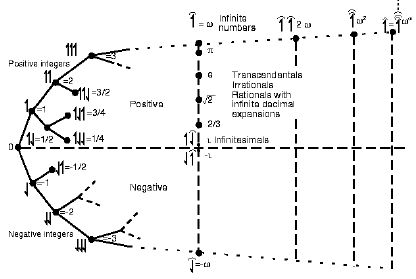
That is interesting, but let us take the reals, R, and define a vector rotation operator i* so that it rotates R through a right angle anticlockwise pivoting on 0. So, any positive x in R is transformed to i*x, along i*R, going upwards. (Yes, the y-axis, oY.) Now, apply i* again, so we see i*i*x = – x, on the negative reals. That is, we have a natural interpretation of i, i.e. i^2 = -1, i is sqrt(-1). The rotating vectors approach makes for a more coherent understanding of so-called imaginary numbers. Thus, complex numbers, C are actually 2-d vectors that help us to do all sorts of interesting things, especially once they get to rotate.
We can go on from here, using power series to define a complex exponential form of the rotating vectors approach, which then yields the famous expression 0 = 1 + e^(i*pi).
All of this then comes back to the Fourier analysis, as the video demonstrates by showing rotating vectors added up tip to tail to form complex wave forms. Which, then points to how we can move freely between the time domain and the frequency domain to better understand phenomena in the real world.
Where, the underlying message clearly is that the logic of structure and quantity — mathematics — is deeply embedded in reality. And no, this is not flogging a dead horse, it is awakening human (as opposed to equine) understanding. END