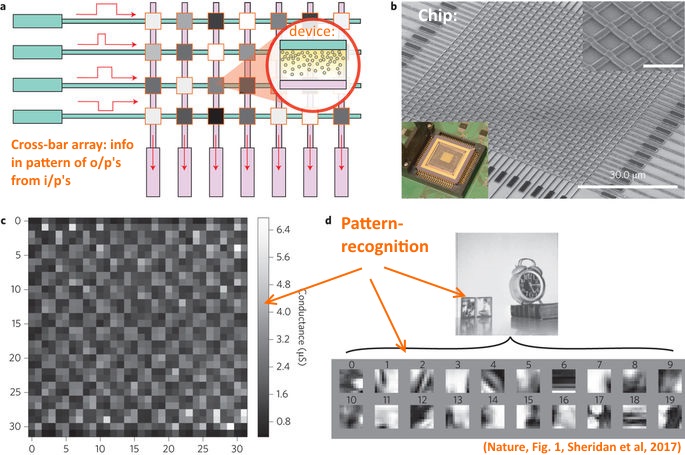
Memristors [= memory + resistors] are a promising memory-based information storage technology that can work as non-volatile memory and in neural networks. They were suggested c. 1971 by Leon Chua, and since HP created a TiO2-based multilayer architecture device exhibiting memristor capabilites in 2007, they have been a focus for research, given their potential.
Here, we may ponder a crossbar array of memristor elements forming a signal-processing matrix:
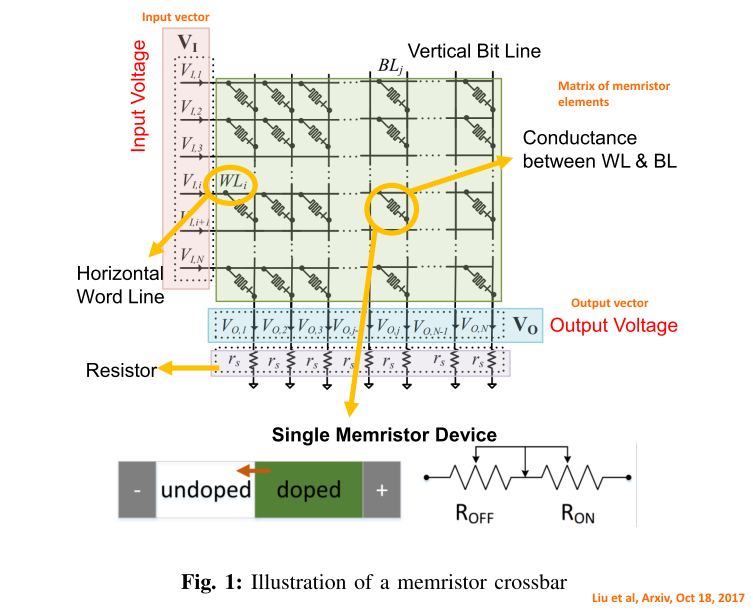
Memristors are of interest to AI as a means to effect neural networks. For instance, a crossbar network (as is illustrated just above) has been used to demonstrate powerful image processing. As Sheridan et al reported in Nature, May 22, 2017 (details pay-walled, of course . . . ):
>>Sparse representation of information provides a powerful means to perform feature extraction on high-dimensional data and is of broad interest for applications in signal processing, computer vision, object recognition and neurobiology. Sparse coding is also believed to be a key mechanism by which biological neural systems can efficiently process a large amount of complex sensory data while consuming very little power. Here, we report the experimental implementation of sparse coding algorithms in a bio-inspired approach using a 32 × 32 crossbar array of analog memristors. This network enables efficient implementation of pattern matching and lateral neuron inhibition and allows input data to be sparsely encoded using neuron activities and stored dictionary elements.>>
That’s impressive, and of course, as reported, it is using the analogue, continuously variable signal mode.
Liu et al report a perhaps even more interesting result on the power of such arrays to process linear expression arrays:
>>Memristors have recently received significant attention as ubiquitous device-level components for building a novel generation of computing systems. These devices have many promising features, such as non-volatility, low power consumption, high density, and excellent scalability. The ability to control and modify biasing voltages at the two terminals of memristors make them promising candidates to perform matrix-vector multiplications and solve systems of linear equations. In this article, we discuss how networks of memristors arranged in crossbar arrays can be used for efficiently solving optimization and machine learning problems. We introduce a new memristor-based optimization framework that combines the computational merit of memristor crossbars with the advantages of an operator splitting method, alternating direction method of multipliers (ADMM). Here, ADMM helps in splitting a complex optimization problem into subproblems that involve the solution of systems of linear equations. The capability of this framework is shown by applying it to linear programming, quadratic programming, and sparse optimization. In addition to ADMM, implementation of a customized power iteration (PI) method for eigenvalue/eigenvector computation using memristor crossbars is discussed. The memristor-based PI method can further be applied to principal component analysis (PCA). The use of memristor crossbars yields a significant speed-up in computation, and thus, we believe, has the potential to advance optimization and machine learning research in artificial intelligence (AI). >>
(In looking at this, we should note too that in state space approaches to control systems, matrix elements can be in effect complex domain transfer functions, giving a higher dimension of power to matrix based processing.)
As Liu et al go on:
>>Memristors, nano-scale devices conceived by Leon Chua in 1971, have been physically realized by scientists from Hewlett-Packard [1], [2]. In contrast with the traditional CMOS technology, memristors can be used as non-volatile memories for building brain-like learning machines with memristive synapses [3]. They offer the ability to construct a dense, continuously programmable, and reasonably accurate cross-point array architecture, which can be used for data-intensive applications [4]. For example, a memristor crossbar array exhibits a unique type of parallelism that can be utilized to perform matrix-vector multiplication and solve systems of linear equations in an astonishing O(1) time complexity [5]–[8]. Discovery and physical realization of memristors has inspired the development of efficient approaches to implement neuromorphic computing systems that can mimic neuro-biological architectures and perform high-performance computing for deep neural networks and optimization algorithms [9]. The similarity between the programmable resistance state of memristors and the variable synaptic strengths of biological synapses facilitates the circuit realization of neural network models [10]. Nowadays, an artificial neural network has become an extremely popular machine learning tool with a wide spectrum of applications, ranging from prediction/classification, computer vision, natural language processing, image processing, to signal processing [11].>>
They also remark, tying in the general hill-climbing [in, steepest descent form] approach commonly discussed in optimisation:
>>a general question to be answered in this context is: how can one design a general memristor-based computation framework to accelerate the optimization procedure? The interior-point algorithm is one of the most commonly-used optimization approaches implemented in software. It begins at an interior point within the feasible region, then applies a projective transformation so that the current interior point is the center of projective space, and then moves in the direction of the steepest descent [37]. However, the inherent hardware limitations prevent the direct mapping from the interior-point algorithm to memristor crossbars. First, a memristor crossbar only allows square matrices with nonnegative entries during computation, since the memristance is always nonnegative. Second, the memristor crossbar suffers from hardware variations, which degrade the reading/writing accuracy of memristor crossbars.>>
Their solution is to use additional memristors to represent negative values to fix the first problem; involving decomposition into sub-problems. Then, with help of ADMM, the array is programmed just once, to get beyond the hardware variation issue. Using suitable scaling and manipulations, memristors are then set up to carry out matrix multiplication. That is an inherently powerful result as anyone familiar with the ubiquity of matrix models in modern systems analysis of various types will testify.
Reversing the inputs and outputs then sets up a solver that can work in O(1) — constant time, effectively “one step” [with seven-league boots] — computation time, which Liu et al aptly describe as “astonishing.”
Food for thought. END