This morning, in the Gonzalez video post comment exchange, I saw where Mung raised a question about how Young Earth Creationists address the Old Cosmos, Old Earth implications of the view raised.
I thought it useful to respond briefly, but then the wider connexions surfaced.
I would like to stir the pot a bit [–> pl. note the new category], by headlining some sketched out thoughts for consideration, on the mathematical ordering of reality, and related worldviews level philosophical and even theological issues. Indeed, somewhere along the line, the whole project of the validity of a natural theology (and Biblical references to same) crops up as connected to the concerns.
Kindly, consider the below scoop-out from my response to Mung as very much preliminary notes on thoughts in progress, and do help me clarify and correct my thinking:
___________________
>> I hear you, though there are of course at least two YEC responses: (i) the for-argument, where one shows that even if X were so, then “architect-ing” of the cosmos is still credible, and (ii) something like the Humphreys argument of an old cosmos, frozen time, young earth model.
A third is indeed to reject — per scripture-interpretation grounds — the design approach as a variant on old earth theistic evolutionary thought, which is I think (not 100% sure) near to the “[Semi-?]official view” of one or two of the major YEC groups.
We may well argue one way or another on whether such are valid approaches, but they are options open to YEC advocates.
What I find interesting about the design argument — setting aside the YEC issues — is how robust it is against age, multiverse etc speculations, it is almost as if someone wanted to make sure that the cosmos would “speak” to us, whether looked at with an appreciative eye or analysed scientifically and/or mathematically and/or philosophically.
Right now, what is exercising my mind in the background, is the concept of mathematical ordering of the cosmos as a sign of rational mind behind it.
You will recall where I recently started with the empty set {} and then constructed the natural numbers by successively equating {} = 0, {0} = 1, {0, 1} = 2, etc. This of course already brings to bear infinity. We can then define operations and mappings so we have addition, subtraction, equality etc. Then, I moved to the reals by using a Baire-like construction that exploits the properties of decimal fractions [WLOG] by defining ordered points in the interval [0, 1] through a countably infinite tree with ten branches at each forking node in succession 0.abc . . . Such allows us to fill up the continuum between 0 and 1, which is all we need to extend to any continuum.
After that, I had used the i operator concept (where i*i*x = -1*x so we see sqrt -1 playing an important role) to get us to space (and BTW, to angles and rotation in time too, implicitly using the series expansion definitions of e^x, cos x and sin x, where x can in turn be generated as w*t, w angular velocity and t, time). Once we have an interval [0, 1], where it can also be shown that there is some continuous function on a proposed space S that will map points in [0,1] to its points, S is continuous too and is pathwise connected. The space of points (x, i*x) is obviously such as r*e^i*q can span it, r being the magnitude of the vector where r is in [0,1]. In addition, it is possible to iteratively define a Peano space filling curve that in effect allows a moving point — here comes kinematics, the study of motion without regard to forces — to fill it by continuously touring all points in the space. By identifying an orthogonal set of unit vectors i, j, k, and by bringing on board vectors and matrices as usually defined, we are at 3-d space and we are also at kinematics in time long since. For dynamics, we only need to move from points and images to inertial properties and forces across space and time thus momentum and energy. Along the way, calculus enters and gives tools to analyse — or to define — dynamics in the continuum. By this time, we are in familiar territory and can keep going to all of maths and physics in space-time domains.
This would fit in with the effectiveness of mathematics in physical science, as if the world is ordered mathematically in a unified way, then it would follow the logical consequences of those underlying principles and consequent dynamics.
That is, we have here a frame that is at least suggestive of an ordering frame for physical reality: logical, mathematical mind. (And BTW, I find a unifying view of mathematics and moving onwards to physical dynamics helps fill my urge to find coherent unity. I therefore find it satisfying and motivating of explorations. Much moreso than the actual isolated and rather utilitarian way in which I was actually exposed to such things way back. In effect I am reviewing and back-filling, connecting dots etc. I wonder if that failure of unifying vision is a part of the problem we have with Math? And with science? Etc?)
That brings me back to a scripturally based theological point (yes!), as we may see some interesting and empirically testable assertions in Jn 1, Col 1 and Heb 1, i.e. points where three of those heavily packed brief phil statements I recently talked about crop up — I cite AMP:
Jn 1:1 In the beginning [before all time] was the Word ([a –> NB: Word is LOGOS, meaning, communication, rationality himself . . . ] Christ), and the Word was with God, and the Word was God [b]Himself.
2 He was present originally with God.
3 All things were made and came into existence through Him; and without Him was not even one thing made that has come into being. [–> Notice the implied contrast of contingent vs necessary being, and so creation is the zone of the contingent that has a beginning. By contrast, mathematical reality as above is mental and logical, and insofar as it denotes necessary truth and implications of such, is beginningless, held eternally in the mind of God]
4 In Him was Life, and the Life was the Light of men.
5 And the Light shines on in the darkness, for the darkness has never overpowered it [put it out or absorbed it or appropriated it, and is unreceptive to it]. [–> this brings out the moral ordering of the world and the true balance of power]
Col 1:15 [Now] He is the [o]exact likeness of the unseen God [the visible representation of the invisible]; He is the Firstborn of all creation.
16 For it was in Him that all things were created, in heaven and on earth, things seen and things unseen, whether thrones, dominions, rulers, or authorities; all things were created and exist through Him [by His service, intervention] and in and for Him.
17 And He Himself existed before all things, and in Him all things consist (cohere, are held together).
Heb 1:1 In many separate revelations [[a]each of which set forth a portion of the Truth] and in different ways God spoke of old to [our] forefathers in and by the prophets,
2 [But] in [b]the last of these days He has spoken to us in [the person of a] Son [–> Word/Logos again], Whom He appointed Heir and lawful Owner of all things, also by and through Whom He created the worlds and the reaches of space and the ages of time [He made, produced, built, operated, and arranged them in order].
3 He is the sole expression of the glory of God [the Light-being, the [c]out-raying or radiance of the divine], and He is the perfect imprint and very image of [God’s] nature, upholding and maintaining and guiding and propelling the universe by His mighty word of power. [–> Definition of natural law in the perspective of “thinking God’s (creative and sustaining, ordering) thoughts after him”!] When He had by offering Himself accomplished our cleansing of sins and riddance of guilt, He sat down at the right hand of the divine Majesty on high,
4 [Taking a place and rank by which] He Himself became as much superior to angels as the glorious Name (title) which He has inherited is different from and more excellent than theirs.
These contexts are of course historically quite important in Christian theology and in civilisations shaped by such. Indeed, we see here outlined the philosophical theology that shaped the mindset that propelled the scientific revolution by giving confidence that there was an intelligible, coherently rational natural order made and sustained by God, c 1200 – 1700 and which in accordance with our creation mandate, we were commissioned to explore, discover and use for good. Unfortunately, too often, we have abused that order on the one hand to do evil, and on the other, have too often turned the very order into an improper substitute for the creator who stands behind it.
It is against that backdrop that we run into a key pair of texts:
Ps 19:1 The heavens declare the glory of God; and the firmament shows and proclaims His handiwork.
2 Day after day pours forth speech, and night after night shows forth knowledge.
3 There is no speech nor spoken word [from the stars]; their voice is not heard.
4 Yet their voice [in evidence] goes out through all the earth, their sayings to the end of the world . . .
Rom 1:19 For that which is known about God is evident to them and made plain in their inner consciousness, because God [Himself] has shown it to them.
20 For ever since the creation of the world His invisible nature and attributes, that is, His eternal power and divinity, have been made intelligible and clearly discernible in and through the things that have been made (His handiworks). So [men] are without excuse [altogether without any defense or justification],
21 Because when they knew and recognized Him as God, they did not honor and glorify Him as God or give Him thanks. But instead they became futile and [c]godless in their thinking [with vain imaginings, foolish reasoning, and stupid speculations] and their senseless minds were darkened.
22 Claiming to be wise, they became fools [professing to be smart, they made simpletons of themselves].
23 And by them the glory and majesty and excellence of the immortal God were exchanged for and represented by images, resembling mortal man and birds and beasts and reptiles.
24 Therefore God gave them up in the lusts of their [own] hearts to sexual impurity, to the dishonoring of their bodies among themselves [abandoning them to the degrading power of sin],
25 Because they exchanged the truth of God for a lie and worshiped and served the creature rather than the Creator, Who is blessed forever! Amen (so be it).
Now, I find in these an echo of the line of thought I have been exploring, and also some pretty bold, empirically testable claims and implications. We had better believe — on evident track record — that if the evidence had come up that the cosmos is a chaos instead, this would have been cast in the teeth of theists, loud and long.
Instead, we find an ordered, mathematically coherent system of reality of amazing beauty. The reaction? Stridency, or insistence, to dismiss the idea that even possibly, there lies behind reality an ordering highly mathematical-logical mind.
Ooops, I raised another issue there, didn’t I.
God, plainly, is a serious candidate to be a necessary being, and the NB that would be foundational to reality — indeed, inter alia the eternal mind in which eternal necessary truths reside eternally. Especially mathematical ones, of course.
But that brings up a challenge, that there is a logic of contingency vs necessity of being. Contingent beings [CB’s] possibly may not exist, i.e there are possible worlds in which they would not be. Thus, they depend on external enabling causal factors [XEF’s], think of these as “on/off switches” that must be on or the CB cannot begin or be sustained; e.g. the four factors for a fire highlighted through the fire tetrahedron: fuel, heat, oxidiser, chain reaction.
A genuine NB, on the other hand, has no XEF’s, so it would have no beginning and no possibility of ending.
It would be eternal.
So, if we consider a candidate NB (CNB), the issue is whether it is genuine or not: that is, it either exists in all possible worlds (GNB), or it is IMPOSSIBLE (IB), it can exist in no possible world. For example there is no possible world (PW) in which 3 + 2 = 5 will fail, not even a world empty of material objects. (That is guaranteed by the force of the cascade from the empty set up, mental constructs can create a mathematical universe!)
Likewise, there is no possible world in which 2 + 3 = 6, or the like; such is an IB.
This brings us to a significant challenge that faces those who would deny or dismiss the reality of God.
As God is indeed a serious CNB, we have the choice: GNB or IB. Or as has been put elsewhere, if a candidate necessary being is possible, it will be actual. That is, if it can feasibly exist in at least one possible world, it is not impossible and by virtue of the logic, it will not only be in one possible world but all possible worlds, including the actual one.
So, to deny or dismiss God is to imply — one may not be aware of this, of course — that one holds God to be IMPOSSIBLE.
That is a serious logical-metaphysical commitment indeed.
And, on track record of the objectors, one that many such are very reluctant to take up. Indeed, in part the rhetorical tack of projecting an imagined unique burden of proof on theism, and assuming that in default of absolute deductively valid and sound proof they can rest comfortable on the default assumption that God does not exist, is patently fallacious.
I say this, as invariably, we have worldviews that trace to core beliefs as a cluster, about reality, ourselves in it etc. On the “every tub must stand on its own bottom” principle my Grandpa was so fond of, each worldview faces the same challenge of being reasonable and coherent, matching well to and explaining the world as we experience it. So, playing at rhetorical default games in a worldviews foundation context — and I here assert that every worldview has a foundation of some sort (as can be seen from the implications of the abstract chain of warrant A –> B –> C –> . . . entered into once we ask in succession, why accept A, B, C . . . once we also accept that infinite regress is impossible for the finite and fallible such as we are) — is a fallacy.
{Let me insert an illustration:
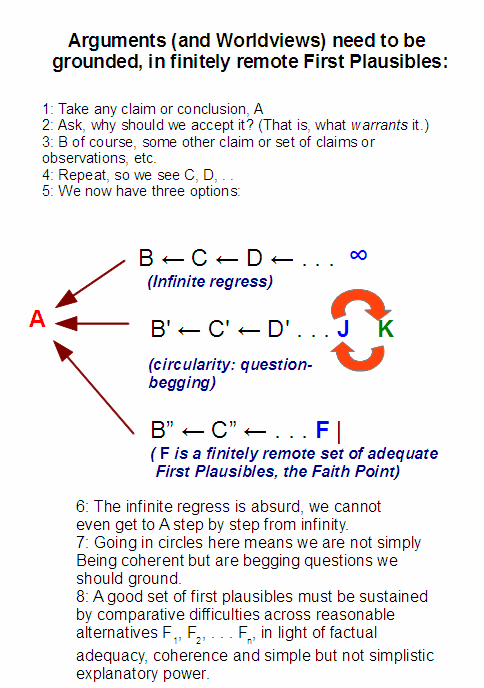
I think some serious re-thinking on worldviews is in order.>>
___________________
Am I on to something here, or am I barking up the wrong tree(s)?
Why or why not? END