(Series)

Emile Borel (1871 – 1956) was a distinguished French Mathematician who — a son of a Minister — came from France’s Protestant minority, and he was a founder of measure theory in mathematics. He was also a significant contributor to modern probability theory, and so Knobloch observed of his approach, that:
>>Borel published more than fifty papers between 1905 and 1950 on the calculus of probability. They were mainly motivated or influenced by Poincaré, Bertrand, Reichenbach, and Keynes. However, he took for the most part an opposed view because of his realistic attitude toward mathematics. He stressed the important and practical value of probability theory. He emphasized the applications to the different sociological, biological, physical, and mathematical sciences. He preferred to elucidate these applications instead of looking for an axiomatization of probability theory. Its essential peculiarities were for him unpredictability, indeterminism, and discontinuity. Nevertheless, he was interested in a clarification of the probability concept. [Emile Borel as a probabilist, in The probabilist revolution Vol 1 (Cambridge Mass., 1987), 215-233. Cited, Mac Tutor History of Mathematics Archive, Borel Biography.]>>
Among other things, he is credited as the worker who introduced a serious mathematical analysis of the so-called Infinite Monkeys theorem (just a moment).
So, it is unsurprising that Abel, in his recent universal plausibility metric paper, observed that:
Emile Borel’s limit of cosmic probabilistic resources [c. 1913?] was only 1050 [[23] (pg. 28-30)]. Borel based this probability bound in part on the product of the number of observable stars (109) times the number of possible human observations that could be made on those stars (1020).
This of course, is now a bit expanded, since the breakthroughs in astronomy occasioned by the Mt Wilson 100-inch telescope under Hubble in the 1920’s. However, it does underscore how centrally important the issue of available resources is, to render a given — logically and physically strictly possible but utterly improbable — potential chance- based event reasonably observable.
We may therefore now introduce Wikipedia as a hostile witness, testifying against known ideological interest, in its article on the Infinite Monkeys theorem:
In one of the forms in which probabilists now know this theorem, with its “dactylographic” [i.e., typewriting] monkeys (French: singes dactylographes; the French word singe covers both the monkeys and the apes), appeared in Émile Borel‘s 1913 article “Mécanique Statistique et Irréversibilité” (Statistical mechanics and irreversibility),[3] and in his book “Le Hasard” in 1914. His “monkeys” are not actual monkeys; rather, they are a metaphor for an imaginary way to produce a large, random sequence of letters. Borel said that if a million monkeys typed ten hours a day, it was extremely unlikely that their output would exactly equal all the books of the richest libraries of the world; and yet, in comparison, it was even more unlikely that the laws of statistical mechanics would ever be violated, even briefly.
The physicist Arthur Eddington drew on Borel’s image further in The Nature of the Physical World (1928), writing:
If I let my fingers wander idly over the keys of a typewriter it might happen that my screed made an intelligible sentence. If an army of monkeys were strumming on typewriters they might write all the books in the British Museum. The chance of their doing so is decidedly more favourable than the chance of the molecules returning to one half of the vessel.[4]
These images invite the reader to consider the incredible improbability of a large but finite number of monkeys working for a large but finite amount of time producing a significant work, and compare this with the even greater improbability of certain physical events. Any physical process that is even less likely than such monkeys’ success is effectively impossible, and it may safely be said that such a process will never happen.
Let us emphasise that last part, as it is so easy to overlook in the heat of the ongoing debates over origins and the significance of the idea that we can infer to design on noticing certain empirical signs:
These images invite the reader to consider the incredible improbability of a large but finite number of monkeys working for a large but finite amount of time producing a significant work, and compare this with the even greater improbability of certain physical events. Any physical process that is even less likely than such monkeys’ success is effectively impossible, and it may safely be said that such a process will never happen.
Why is that?
Because of the nature of sampling from a large space of possible configurations. That is, we face a needle-in-the-haystack challenge.
For, there are only so many resources available in a realistic situation, and only so many observations can therefore be actualised in the time available. As a result, if one is confined to a blind probabilistic, random search process, s/he will soon enough run into the issue that:
a: IF a narrow and atypical set of possible outcomes T, that
b: may be described by some definite specification Z (that does not boil down to listing the set T or the like), and
c: which comprise a set of possibilities E1, E2, . . . En, from
d: a much larger set of possible outcomes, W, THEN:
e: IF, further, we do see some Ei from T, THEN also
f: Ei is not plausibly a chance occurrence.
The reason for this is not hard to spot: when a sufficiently small, chance based, blind sample is taken from a set of possibilities, W — a configuration space, the likeliest outcome is that what is typical of the bulk of the possibilities will be chosen, not what is atypical. And, this is the foundation-stone of the statistical form of the second law of thermodynamics.
Hence, Borel’s remark as summarised by Wikipedia:
Borel said that if a million monkeys typed ten hours a day, it was extremely unlikely that their output would exactly equal all the books of the richest libraries of the world; and yet, in comparison, it was even more unlikely that the laws of statistical mechanics would ever be violated, even briefly.
In recent months, here at UD, we have described this in terms of searching for a needle in a vast haystack [corrective u/d follows]:
let us work back from how it takes ~ 10^30 Planck time states for the fastest chemical reactions, and use this as a yardstick, i.e. in 10^17 s, our solar system’s 10^57 atoms would undergo ~ 10^87 “chemical time” states, about as fast as anything involving atoms could happen. That is 1 in 10^63 of 10^150. So, let’s do an illustrative haystack calculation:
Let us take a straw as weighing about a gram and having comparable density to water, so that a haystack weighing 10^63 g [= 10^57 tonnes] would take up as many cubic metres. The stack, assuming a cubical shape, would be 10^19 m across. Now, 1 light year = 9.46 * 10^15 m, or about 1/1,000 of that distance across. If we were to superpose such a notional 1,000 light years on the side haystack on the zone of space centred on the sun, and leave in all stars, planets, comets, rocks, etc, and take a random sample equal in size to one straw, by absolutely overwhelming odds, we would get straw, not star or planet etc. That is, such a sample would be overwhelmingly likely to reflect the bulk of the distribution, not special, isolated zones in it.
With this in mind, we may now look at the Dembski Chi metric, and reduce it to a simpler, more practically applicable form:
m: In 2005, Dembski provided a fairly complex formula, that we can quote and simplify:
χ = – log2[10^120 ·ϕS(T)·P(T|H)]. χ is “chi” and ϕ is “phi”
n: To simplify and build a more “practical” mathematical model, we note that information theory researchers Shannon and Hartley showed us how to measure information by changing probability into a log measure that allows pieces of information to add up naturally: Ip = – log p, in bits if the base is 2. (That is where the now familiar unit, the bit, comes from.)
o: So, since 10^120 ~ 2^398, we may do some algebra as log(p*q*r) = log(p) + log(q ) + log(r) and log(1/p) = – log (p):
Chi = – log2(2^398 * D2 * p), in bits
Chi = Ip – (398 + K2), where log2 (D2 ) = K2
p: But since 398 + K2 tends to at most 500 bits on the gamut of our solar system [our practical universe, for chemical interactions! (if you want , 1,000 bits would be a limit for the observable cosmos)] and
q: as we can define a dummy variable for specificity, S, where S = 1 or 0 according as the observed configuration, E, is on objective analysis specific to a narrow and independently describable zone of interest, T:
Chi_500 = Ip*S – 500, in bits beyond a “complex enough” threshold
(If S = 0, Chi = – 500, and, if Ip is less than 500 bits, Chi will be negative even if S is positive. E.g.: A string of 501 coins tossed at random will have S = 0, but if the coins are arranged to spell out a message in English using the ASCII code [[notice independent specification of a narrow zone of possible configurations, T], Chi will — unsurprisingly — be positive.)
r: So, we have some reason to suggest that if something, E, is based on specific information describable in a way that does not just quote E and requires at least 500 specific bits to store the specific information, then the most reasonable explanation for the cause of E is that it was intelligently designed. (For instance, no-one would dream of asserting seriously that the English text of this post is a matter of chance occurrence giving rise to a lucky configuration, a point that was well-understood by that Bible-thumping redneck fundy — NOT! — Cicero in 50 BC.)
s: The metric may be directly applied to biological cases:
t: Using Durston’s Fits values — functionally specific bits — from his Table 1, to quantify I, so also accepting functionality on specific sequences as showing specificity giving S = 1, we may apply the simplified Chi_500 metric of bits beyond the threshold:
RecA: 242 AA, 832 fits, Chi: 332 bits beyond
SecY: 342 AA, 688 fits, Chi: 188 bits beyond
Corona S2: 445 AA, 1285 fits, Chi: 785 bits beyond
u: And, this raises the controversial question that biological examples such as DNA — which in a living cell is much more complex than 500 bits — may be designed to carry out particular functions in the cell and the wider organism.
v: Therefore, we have at least one possible general empirical sign of intelligent design, namely: functionally specific, complex organisation and associated information [[FSCO/I] .
But, but, but . . . isn’t “natural selection” precisely NOT a chance based process, so doesn’t the ability to reproduce in environments and adapt to new niches then dominate the population make nonsense of such a calculation?
NO.
Why is that?
Because of the actual claimed source of variation (which is often masked by the emphasis on “selection”) and the scope of innovations required to originate functionally effective body plans, as opposed to varying same — starting with the very first one, i.e. Origin of Life, OOL.
But that’s Hoyle’s fallacy!
Advice: when you go up against a Nobel-equivalent prize-holder, whose field requires expertise in mathematics and thermodynamics, one would be well advised to examine carefully the underpinnings of what is being said, not just the rhetorical flourish about tornadoes in junkyards in Seattle assembling 747 Jumbo Jets.
More specifically, the key concept of Darwinian evolution [we need not detain ourselves too much on debates over mutations as the way variations manifest themselves], is that:
CHANCE VARIATION (CV) + NATURAL “SELECTION” (NS) –> DESCENT WITH (UNLIMITED) MODIFICATION (DWM), i.e. “EVOLUTION.”
CV + NS –> DWM, aka Evolution
If we look at NS, this boils down to differential reproductive success in environments leading to elimination of the relatively unfit.
That is, NS is a culling-out process, a subtract-er of information, not the claimed source of information.
That leaves only CV, i.e. blind chance, manifested in various ways. (And of course, in anticipation of some of the usual side-tracks, we must note that the Darwinian view, as modified though the genetic mutations concept and population genetics to describe how population fractions shift, is the dominant view in the field.)
There are of course some empirical cases in point, but in all these cases, what is observed is fairly minor variations within a given body plan, not the relevant issue: the spontaneous emergence of such a complex, functionally specific and tightly integrated body plan, which must be viable from the zygote on up.
To cover that gap, we have a well-known metaphorical image — an analogy, the Darwinian Tree of Life. This boils down to implying that there is a vast contiguous continent of functionally possible variations of life forms, so that we may see a smooth incremental development across that vast fitness landscape, once we had an original life form capable of self-replication.
What is the evidence for that?
Actually, nil.
The fossil record, the only direct empirical evidence of the remote past, is notoriously that of sudden appearances of novel forms, stasis (with some variability within the form obviously), and disappearance and/or continuation into the modern world.
If by contrast the tree of life framework were the observed reality, we would see a fossil record DOMINATED by transitional forms, not the few strained examples that are so often triumphalistically presented in textbooks and museums.
Similarly, it is notorious that fairly minor variations in the embryological development process are easily fatal. No surprise, if we have a highly complex, deeply interwoven interactive system, chance disturbances are overwhelmingly going to be disruptive.
Likewise, complex, functionally specific hardware is not designed and developed by small, chance based functional increments to an existing simple form.
Hoyle’s challenge of overwhelming improbability does not begin with the assembly of a Jumbo jet by chance, it begins with the assembly of say an indicating instrument on its cockpit instrument panel.
(Indeed, it would be utterly unlikely for a large box of mixed nuts and bolts, to by chance shaking, bring together matching nut and bolt and screw them together tightly; the first step to assembling the instrument by chance.)
Further to this, It would be bad enough to try to get together the text strings for a Hello World program (let’s leave off the implementing machinery and software that make it work) by chance. To then incrementally create an operating system from it, each small step along the way being functional, would be a bizarrely operationally impossible super-task.
So, the real challenge is that those who have put forth the tree of life, continent of function type approach, have got to show, empirically that their step by step path up the slopes of Mt Improbable, are empirically observable, at least in reasonable model cases. And, they need to show that in effect chance variations on a Hello World will lead, within reasonable plausibility, to such a stepwise development that transforms the Hello World into something fundamentally different.
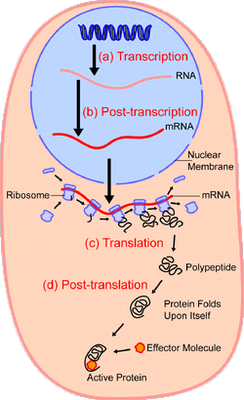
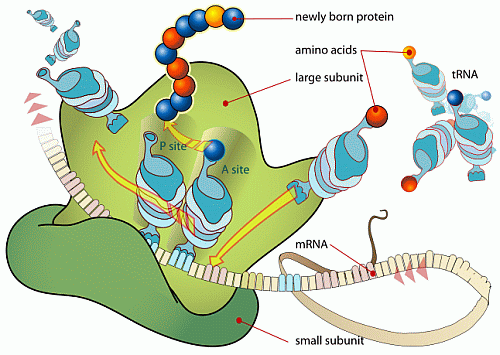
In short, we have excellent reason to infer that — absent empirical demonstration otherwise — complex specifically functional integrated complex organisation arises in clusters that are atypical of the general run of the vastly larger set of physically possible configurations of components. And, the strongest pointer that this is plainly so for life forms as well, is the detailed, complex, step by step information controlled nature of the processes in the cell that use information stored in DNA to make proteins. Let’s call Wiki as a hostile witness again, courtesy two key diagrams:
I: Overview:
II: Focusing on the Ribosome in action for protein synthesis:
Clay animation video [added Dec 4]:
[youtube OEJ0GWAoSYY]
More detailed animation [added Dec 4]:
[vimeo 31830891]
This sort of elaborate, tightly controlled, instruction based step by step process is itself a strong sign that this sort of outcome is unlikely by chance variations.
(And, attempts to deny the obvious, that we are looking at digital information at work in algorithmic, step by step processes, is itself a sign that there is a controlling a priori at work that must lock out the very evidence before our eyes to succeed. The above is not intended to persuade such, they are plainly not open to evidence, so we can only note how their position reduces to patent absurdity in the face of evidence and move on.)
But, isn’t the insertion of a dummy variable S into the Chi_500 metric little more than question-begging?
Again, NO.
Let us consider a simple form of the per-aspect explanatory filter approach:
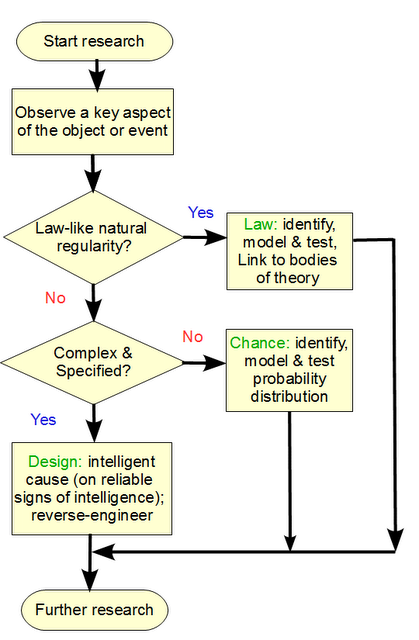
You will observe two key decision nodes, where the first default is that the aspect of the object, phenomenon or process being studied, is rooted in a natural, lawlike regularity that under similar conditions will produce similar outcomes, i.e there is a reliable law of nature at work, leading to low contingency of outcomes. A dropped, heavy object near earth’s surface will reliably fall at g initial acceleration, 9.8 m/s2. That lawlike behaviour with low contingency can be empirically investigated and would eliminate design as a reasonable explanation.
Second, we see some situations where there is a high degree of contingency of possible outcomes under initial circumstances. This is the more interesting case, and in our experience has two candidate mechanisms: chance, or choice. The default for S under these circumstances, is 0. That is, the presumption is that chance is an adequate explanation, unless there is a good — empirical and/or analytical — reason to think otherwise. In short, on investigation of the dynamics of volcanoes and our experience with them, rooted in direct observations, the complexity of a Mt Pinatubo is explained partly on natural laws and chance variations, there is no need to infer to choice to explain its structure.
But, if the observed configurations of highly contingent elements were from a narrow and atypical zone T not credibly reachable based on the search resources available, then we would be objectively warranted to infer to choice. For instance, a chance based text string of length equal to this post, would overwhelmingly be gibberish, so we are entitled to note the functional specificity at work in the post, and assign S = 1 here.
So, the dummy variable S is not a matter of question-begging, never mind the usual dismissive talking points.
I is of course an information measure based on standard approaches, through the sort of probabilistic calculations Hartley and Shannon used, or by a direct observation of the state-structure of a system [e.g. on/off switches naturally encode one bit each].
And, where an entity is not a direct information storing object, we may reduce it to a mesh of nodes and arcs, then investigate how much variation can be allowed and still retain adequate function, i.e. a key and lock can be reduced to a bit measure of implied information, and a sculpture like at Mt Rushmore can similarly be analysed, given the specificity of portraiture.
The 500 is a threshold, related to the limits of the search resources of our solar system, and if we want more, we can easily move up to the 1,000 bit threshold for our observed cosmos.
On needle in a haystack grounds, or monkeys strumming at the keyboards grounds, if we are dealing with functionally specific, complex information beyond these thresholds, the best explanation for seeing such is design.
And, that is abundantly verified by the contents of say the Library of Congress (26 million works) or the Internet, or the product across time of the Computer programming industry.
But, what about Genetic Algorithms etc, don’t they prove that such FSCI can come about by cumulative progress based on trial and error rewarded by success?
Not really.
As a rule, such are about generalised hill-climbing within islands of function characterised by intelligently designed fitness functions with well-behaved trends and controlled variation within equally intelligently designed search algorithms. They start within a target Zone T, by design, and proceed to adapt incrementally based on built in designed algorithms.
If such a GA were to emerge from a Hello World by incremental chance variations that worked as programs in their own right every step of the way, that would be a different story, but for excellent reason we can safely include GAs in the set of cases where FSCI comes about by choice, not chance.
So, we can see what the Chi_500 expression means, and how it is a reasonable and empirically supported tool for measuring complex specified information, especially where the specification is functionally based.
And, we can see the basis for what it is doing, and why one is justified to use it, despite many commonly encountered objections. END
________
F/N, Jan 22: In response to a renewed controversy tangential to another blog thread, I have redirected discussion here. As a point of reference for background information, I append a clip from the thread:
. . . [If you wish to find] basic background on info theory and similar background from serious sources, then go to the linked thread . . . And BTW, Shannon’s original 1948 paper is still a good early stop-off on this. I just did a web search and see it is surprisingly hard to get a good simple free online 101 on info theory for the non mathematically sophisticated; to my astonishment the section A of my always linked note clipped from above is by comparison a fairly useful first intro. I like this intro at the next level here, this is similar, this is nice and short while introducing notation, this is a short book in effect, this is a longer one, and I suggest the Marks lecture on evo informatics here as a useful contextualisation. Qualitative outline here. I note as well Perry Marshall’s related exchange here, to save going over long since adequately answered talking points, such as asserting that DNA in the context of genes is not coded information expressed in a string of 4-state per position G/C/A/T monomers. The one good thing is, I found the Jaynes 1957 paper online, now added to my vault, no cloud without a silver lining.
If you are genuinely puzzled on practical heuristics, I suggest a look at the geoglyphs example already linked. This genetic discussion may help on the basic ideas, but of course the issues Durston et al raised in 2007 are not delved on.
(I must note that an industry-full of complex praxis is going to be hard to reduce to an in a nutshell. However, we are quite familiar with information at work, and how we routinely measure it as in say the familiar: “this Word file is 235 k bytes.” That such a file is exceedingly functionally specific can be seen by the experiment of opening one up in an inspection package that will access raw text symbols for the file. A lot of it will look like repetitive nonsense, but if you clip off such, sometimes just one header character, the file will be corrupted and will not open as a Word file. When we have a great many parts that must be right and in the right pattern for something to work in a given context like this, we are dealing with functionally specific, complex organisation and associated information, FSCO/I for short.
The point of the main post above is that once we have this, and are past 500 bits or 1000 bits, it is not credible that such can arise by blind chance and mechanical necessity. But of course, intelligence routinely produces such, like comments in this thread. Objectors can answer all of this quite simply, by producing a case where such chance and necessity — without intelligent action by the back door — produces such FSCO/I. If they could do this, the heart would be cut out of design theory. But, year after year, thread after thread, here and elsewhere, this simple challenge is not being met. Borel, as discussed above, points out the basic reason why.