From Natalie Wolchover at Quanta:
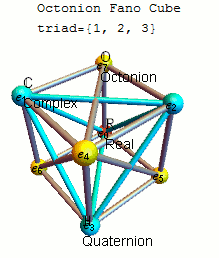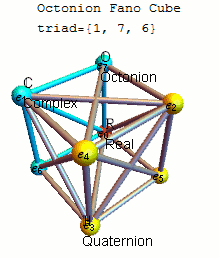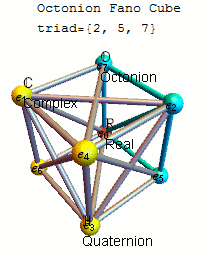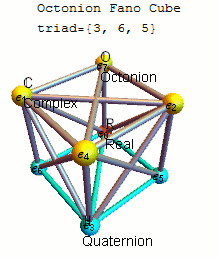
Complex numbers, suitably paired, form 4-D “quaternions,” discovered in 1843 by the Irish mathematician William Rowan Hamilton, who on the spot ecstatically chiseled the formula into Dublin’s Broome Bridge. John Graves, a lawyer friend of Hamilton’s, subsequently showed that pairs of quaternions make octonions: numbers that define coordinates in an abstract 8-D space.
Matemaical approaches to physics were left behind during the pursuit of answers from collides but, as Wolchover writes, no particles beyond the Standard (Big Bang) model have been found.” One rearcher, Cohl Fury,
has since produced a number of results connecting the octonions to the Standard Model that experts are calling intriguing, curious, elegant and novel. “She has taken significant steps toward solving some really deep physical puzzles,” said Shadi Tahvildar-Zadeh, a mathematical physicist at Rutgers University who recently visited Furey in Cambridge after watching an online series of lecture videos she made about her work.
Furey has yet to construct a simple octonionic model of all Standard Model particles and forces in one go, and she hasn’t touched on gravity.
Yes, gravity is the tough one. But this is fun:
When you double the dimensions with each step as you go from real numbers to complex numbers to quaternions to octonions, she explained, “in every step you lose a property.” Real numbers can be ordered from smallest to largest, for instance, “whereas in the complex plane there’s no such concept.” Next, quaternions lose commutativity; for them, a × b doesn’t equal b × a. This makes sense, since multiplying higher-dimensional numbers involves rotation, and when you switch the order of rotations in more than two dimensions you end up in a different place. Much more bizarrely, the octonions are nonassociative, meaning (a × b) × c doesn’t equal a × (b × c). More.
For more number fun, see also: At Vox the number zero is weird
Is celeb number pi a “normal” number? Not normal. And things get worse. Surely this oddity is related in some way to the unreasonable effectiveness of mathematics.
Here’s some zero fun: Is zero even?
and
Must we understand “nothing” to understand physics?