While most people agree that simple laws/rules per se cannot create information, some believe that algorithms are capable to do that. This seems an odd idea, because algorithms, i.e. sets of instructions, after all can be considered complex laws/rules, or set of rules, sort of generalizations of rules.
The usual and simplest example some evolutionists offer to prove that algorithms can produce information is a stochastic algorithm that, by randomly choosing characters from the English alphabet, in a number of trials, finally outputs the phrase “methinks it is like a weasel” (or whatever else phrase with meaning). This way it seems to them that information is produced by randomness + laws, or even created from nothing. Let’s admit for the sake of argument that the phrase “methinks it is like a weasel” so produced is information. The questions are: (1) is that truly creation of information from nothing? (2) what really produces it?
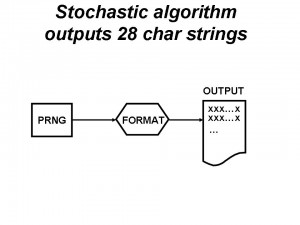
Consider the following schema of such algorithm:
We have on the left a pseudo random number generator PRNG (like the Mersenne twister) that provides random numbers. In the middle, a set of instructions labelled “FORMAT” take the numbers, convert them in characters of the English alphabet (26 characters + space), and finally format them in a series of 28 character long strings listed vertically on a file (on the right). The total possible 28 character strings are Os = ~1.2*10^40 corresponding to a Shannon information of near Oi = ~4.5*10^42 bits. Only a very small subset of those strings are English sentences with a meaning (an interpolation based on a power law says Es = ~10^9 sentences). Therefore a very reduced amount of those combinatorial Shannon bits Oi is meaningful English information Ei = ~4.2*10^10 bits. (By the way, the recognition of the English sentences is a job requiring a linguistic intelligence – both in the syntax and semantics sense – that is hard to simulate mechanistically.)
Here we are interested in the asymptotic behaviour of the system, that is how it works when the running time tends to infinity. Given enough time our algorithm will output all possible 28 char strings and all 28 letter English sentences (“methinks it is like a weasel” included). If the program runs 10^29 seconds (10^12 times the age of the universe) on the fastest computer available today it will output ~10^41 sequences and any given sequence has 0.99976 probability of occurring. Considering the asymptotic behaviour, let’s finally wonder where Ei comes from.
Ei comes from the potentiality that the system contains just from the beginning. This potentiality is somehow front-loaded in the system and develops when the system is running. The potentiality will develop partially or totally dependently from the running time. The information potentiality, measured in Shannon sense is Oi bits, measured in English sense is Ei bits, as shown before. This system (as any closed system) cannot unfold more than its potentiality allows, because, after the production of Os, the sequences repeat and no new sequence is produced. The potentiality is entirely accounted for by the instructions pre-loaded in the algorithm (and obviously by the pre-existent computing environment available to run the program). These instructions (hosted and processed by the informatics infrastructure) define, in a compress way, the potentiality and how it can develop. About the concept of potentiality see here.
Answer to #2 question: given such potentiality is entirely due to the program (plus the computer), what really produces Ei is not the algorithm, rather the cause of its design, the designer. The information provided by the designer exactly accounts for what the program actually does, what the program could potentially do, and its asymptotic tendency. The programmer provides all information in potential/compressed form by design just from the beginning, then the algorithm per se creates zero information. Since the algorithm and its potentiality come from their programmer, also Ei comes from the programmer. The algorithm, its potentiality and all effectively produced (or potentially producible) strings are due to the system designer. The guidance given by the programmer is exactly the program, no more no less.
Therefore one can say that nothing new can be produced that isn’t already there. Nowhere there is something coming from nothing. Nowhere there is more arising from less. No “free-lunch”, as ID theory puts it.
At this point a Darwinist could argue: “since your example of randomness + laws creating information is analogous to my chance + necessity creating organisms, yourself have proved that Darwinism can work”. This argumentation is flawed for two main reasons:
(a) the stochastic system I described is entirely designed;
(b) organisms contain advanced organization, a far higher and qualitative thing, whose vertical hierarchical functional complex specified information is incomparable to the horizontal flat serialization of characters produced by my algorithm.
But this is a point worth of analysis in another thread.