Selensky, Shallit, & Koza vs artificial life simulations

It’s always a pleasure to host Dr Selensky’s thoughtful contributions. Here, he tackles the subject of artificial life simulations and the implications of modelling environments, assumptions, algorithms etc:

____________________________

On Modelling Spontaneous Emergence of Programs and Their Evolutionary Self-Improvement

Evgeny Selensky

Some time ago, I left a comment on Jeffrey Shallit’s blog. We exchanged a couple of phrases. In particular, I referred Jeffrey to the requirement for computational halting in models of artificial life. I praised David Abel’s work, which put him off. In response, Jeffrey recommended that I should “read and understand” the following article. I have done my homework now. However I’d like to post here at UD rather than visit Jeffrey’s blog again. Jeffrey of course is welcome to respond to my note here. My thoughts about the paper follow.

John R. Koza: Spontaneous Emergence of Self-Replicating and Evolutionarily Self-Improving Computer Programs. In: Proceedings of the Third Workshop on Artificial Life (ALIFE-3), 1993. [Link.]

The article, a quite old one now, proposes a mathematical model that, the author believes, justifies an affirmative answer regarding both:

1. the possibility of spontaneous generation of self-replicating code; and
2. its subsequent evolutionary self-correction.

The author analyses the possibility of spontaneous generation of computer code that can replicate itself from one or two parent programs as well as evolutionarily self-correct given enough primitive computational elements at the start. It is assumed that the primitive computational elements interact and collectively are Turing complete. Among other things, elements can form agglomerations.

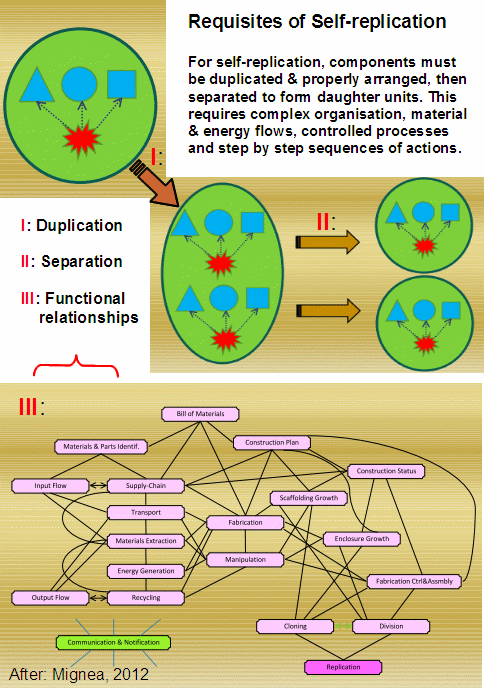
Mathematical modelling allows one to create a virtual world with its own laws. We need therefore to be careful applying conclusions from mathematical modelling in the real world. Any such conclusions must be taken in with a pinch of salt. Even to model something that can allegedly spontaneously emerge, one needs an intelligently set experimental (computational) environment: a programmer (sometimes even a whole team), a complex computational system and intelligent active control of the experiment (broadly speaking, the knowledge how and when to change the algorithm parameter settings and how to guide the search for solutions). Ironically, the relevant branch of computer science is called artificial life whose objective is to demonstrate that biological life is just a simple consequence of a dozen or two of automatic rules given some basic assumptions (it all of course depends what the assumptions are); and that, once such rules are defined and applied to an initial population of self-reproducing organisms, everything else is settled. Well, yes in terms of cellular automata; probably not in terms of it being responsible for all observed biological complexity. In theory, there is no upper bound on the complexity of things that evolution can produce (at least I am not aware of any, other than natural limitations such as the amount of available resource, mutation and reproduction rates, etc.). And yet experience shows that unless one guides the search from outside, nothing genuinely novel and functionally complex can come out of it. Having said this, let’s have a look what the article has to say.

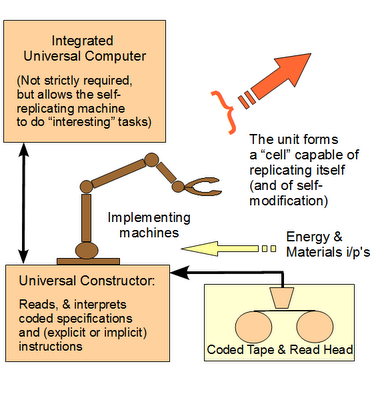
As usual in such papers, the trick is in the power of the starting assumptions and methodology. That evolution occurs in reality is nothing new: as soon as there is an initial population of open-ended self-replicating systems, its evolutionary behaviour is inevitable. Heritable differences in characteristics of individuals will necessitate a selective pressure from the environment, which will cause differential reproduction. Fine. However, the question is, firstly, to what extent we can rely on the conclusions from this or similar computational studies in matters concerning real phenomena such as biological evolution, and how general those conclusions are in real life.

The model kicks off from a starting configuration (the so-called primordial sea of primitive computational elements) given a Turing complete set of functions encoded by the elements. At any instant, a single program is searching for other programs from among its neighbours. The objective is to find self-reproducing programs able to self-improve over generations. The search looks through programs from among those in the sea that are neighbours to the program currently executing. The neighbourhood of a program is changing over time. A neighbour program is selected to execute next if it matches parts of the program currently running. The search terminates as soon as all programs have been run. In practice, however, the process has to be stopped after a few generations because the computational resources get exhausted. The total number of programs may grow over time. Overall, the model actually uses intelligent artificially guided search instead of blind Darwinian search.

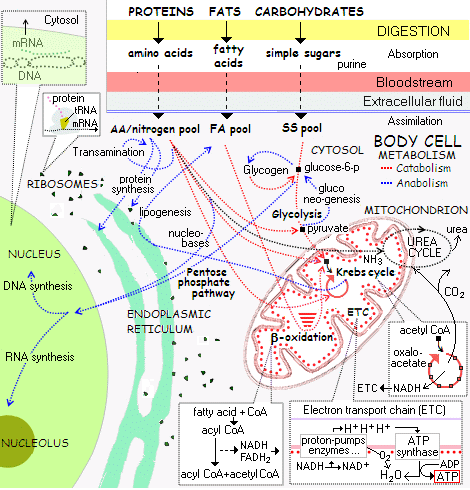
[Overnight, let me insert an overview of the metabolic framework of cell-based life, using a compressed form of the typical wall-sized chart, to illustrate what has to be answered to:]

[Also, let me expand the top left corner, zooming in on Protein Synthesis:]

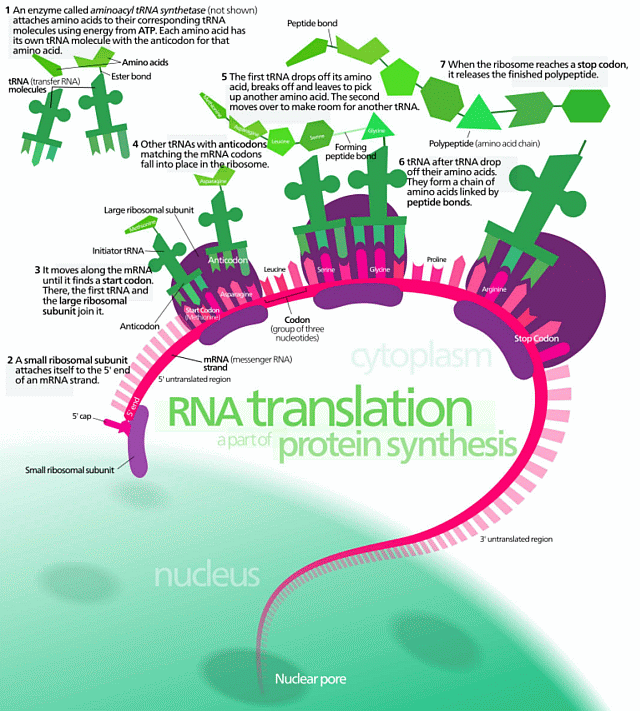
[And while we are at it, here is Yockey’s summary of the implied communication system involved, an irreducibly complex entity:]

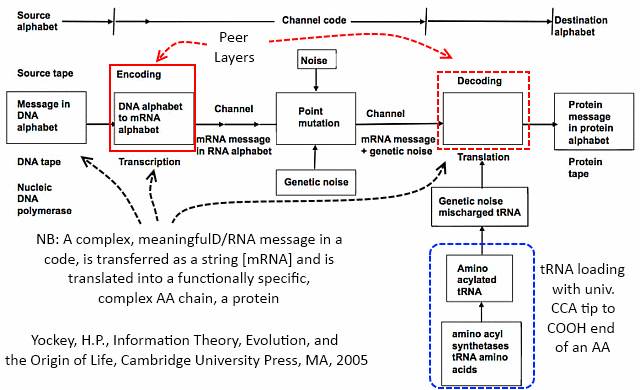
Now the details:

• The paper assumes the presence of a primordial sea composed of a given number of primitive computational elements that model some basic functions of organic molecules. Although the presence of a population of primitive computational elements is taken for granted, one should not forget that the physical laws are not the same as the rules of operation of a computer. The first have physical necessity underpinning it whereas the second is due to some arbitrary logical (i.e. non-physical) correspondence between symbol (a physical token) and meaning (a physical effect). We cannot assume therefore that physical or chemical properties of matter (e.g. properties of carbon or oxygen) are analogous to the behaviour of a computer. This is the weakest point of any paper of this sort simply because drawing such an analogy between the physical laws and the logical rules is unwarranted. As American philosopher Alex Rosenberg put it, in our world no clump of matter is about any other clump of matter. On the contrary, information translation whereby one configuration of matter represents another configuration of matter is the unique property of two kinds of systems: (a) natural human languages or artificial linguistic systems such as mathematics or programming languages and (b) biological systems. Consequently, the most important question is, how the first population of information translators (i.e. physical embodiments of the data-protocol-interpreter tuple) came about. Clearly, computer code generated by some basic routine of a computational element must be syntactically correct to be interpreted correctly; otherwise generated ‘code’ is not code in the true sense but meaningless gibberish.
• Next, the modified (generated) code needs to terminate in reasonable time, hence the need for a halting oracle, which I alluded to in the chat with Jeffrey. In the paper, a limit on the number of nested loops is imposed explicitly. “If the program fails to terminate for any reason within a reasonable number of steps or the symbols […] do not form a valid program”, the program is terminated by force. Recall Gregory Chaitin’s meta-life model [Chaitin 2011] where the programmer essentially acted as a halting oracle, and the computational resources were not considered limited; its critique can be found in [Ewert et. al 2013], a more informal accounts are here and here. Coming back to John Koza’s model, consequently, the efficiency of search is implicitly biased in favour of desired states. Note that syntactic rules are checked explicitly, which is also a means of implicitly biasing the experiments towards desired results.
• There exist different types of complexity in relation to biopolymers (and consequently to the primitive computational elements of the model the paper proposes) [Abel, 2011]:
  • random sequence complexity (RSC) exemplified by a string of symbols whereby every symbol is equiprobable at each position in the string; this type of sequence represents chaotic structures of stochastic origin that are unconstrained by natural law or voluntary act of an agent;
  • ordered sequence complexity (OSC) whereby a string of symbols represents structures patterned either by natural regularities or some statistically weighted means (but again rather not by deliberate choice on the part of an agent);
  • functional sequence complexity (FSC) representing prescription whereby each symbol in a sequence is a result of a specific purposeful selection to encode a function. Functional sequences are physically arbitrary (indifferent, energy-degenerate) and are constrained by choices from an agent. It has been shown that only human languages, mathematics, computer code or biological polymers exhibit statistically significant levels of FSC [Abel 2011].
• Clearly, the paper models the process of generating strings that exhibit high levels of FSC. The (Turing complete) set of primitive elements is selected such that they can already perform the basic functions. What the search is set to achieve is creating their agglomerations and in carefully control manner by collecting the initial pool of self-replicators with the “right” properties. In fact, the paper demonstrates a kind of game using a set of basic rules with a clearly defined goal: to compute for self-reproduction. Evolution in nature does not select for a future function, it selects from among existing functions in the context of a population of self-reproducing organisms competing for limited resources. Actually, even that is a metaphor because active selection is not what happens in nature. What is called selection in nature is rather a consequence of differential reproduction in the given environmental conditions. And so there is no active control as such in real life. However, in the model active control is everything. There is consequently a significant mismatch between the model and reality. Careful control and stages of selection of individual programs are in place to make sure that something presented as spontaneous emergence happens. Simply saying that this is analogous to what takes place in nature is not convincing.
• In addition to that, in real environments processes are accompanied by noise, which the model does not take into account.
• In the model, a function is evolutionarily gained by inclusion of a new neighbouring computational element from the sea based on matching the selection criteria at time t. What the paper calls a new evolutionarily gained function may not be novel. E.g. if the program before such inclusion had one function of type A but has acquired another function of the same type A as a result of inclusion from the sea, the second one is still regarded as new even though this may not contribute to any actual functional novelty. This inclusion only makes sense in the model in view of an explicit future goal state, self-reproduction, for which the model selects.
• In practice, if the search for solutions is to be of any practical value, the programmer needs to guide the search process. Models relying on blind search are not efficient in practice. “Genetic algorithms are widely cited as demonstrating the power of natural selection to produce biological complexity […] Despite their merits, genetic algorithms establish nothing of the sort. Such algorithms succeed not through any intrinsic property of the search algorithm, but rather through incorporating sources of information derived from the programmer’s prior knowledge” [Ewert et al. 2012]. This knowledge is measured as active information that heuristically organizes the search for solutions. Heuristics are rules of thumb that embody expert knowledge of how the search should be organized based on previous experience of solving similar problems.
• Natural selection is nowhere near intelligent selection in efficiency. Natural selection is most efficient and sensitive when selective pressure is acting with respect to a very limited number of traits (optimization criteria). The problem of sensitivity of the selection model in the paper is not addressed. The real questions are: how much active information is passed from the programmer to the algorithm (i.e. information about where in the search space the likelihood of finding “good” solutions is higher) and how it is done in each case. This paper is no exception. Active information is a measure of the extent to which natural selection acting on a population of organisms in real environments is implicitly replaced with artificial intelligent selection by the programmer. The best example of this occurring is genetic algorithms where:
  • The optimization (fitness) function is given explicitly (not so in nature);
  • The programmer can measure with extremely high accuracy the fitness gradient and then can actively control the search based on the value of the gradient (not so in nature);
  • The search is controlled by creating desired neighbourhoods via particular compositions of mutation operators and filtering out early on those no-hoper candidate solutions that the programmer knows would have only adversely affect the next population and wasted computational resources (nature cannot do this; like I said in nature noise is everywhere).
  • Finally, we cannot assume that nature has unlimited computational resources.
• In a word, it is hard to put it better than the author did himself: the controller exists outside of the individuals. Consequently, the proposed model is a model of intelligent artificial selection, not of Darwinian evolution because it uses explicit control by the experimenter. Specifying which rules the elements should encode actively informs the search algorithm how and what to search. In particular, the programmer decides when, after the next element is taken from the neighbourhood, it should be executed and the results analyzed and when the search should only check symbolically if the element has the appropriate structure. Similar rules are in place to control when the program that is being executed start searching its neighbourhood for other programs. If a neighbour program matches a template, the currently executing program can be replaced with a larger program that is an agglomeration of the current one and its neighbour. As expected, the size of programs will tend to grow exponentially. Given that computational resources were necessarily limited this is why some filtering of programs was in place based on size and other parameters.

• Like I said, I agree with the author that because the resources are limited, the existence of a population of differing self-reproducing open-ended systems automatically entails selection pressure and consequently evolution. Nonetheless, the scope of evolutionary movement in the phase space will be limited in practice by a whole range of key biological factors. The practical limits of evolvability are therefore determined by what is biologically feasible. As a result the areas in the phase space of a living system that are evolutionarily reachable from a given initial point are necessarily limited. Therefore, instead of a continent of function, biological systems are confined to evolve in islands/pockets of function; while the borders cannot be crossed. They may well change over time and some islands may perhaps even merge or new islands may form. But that does not resolve the problem of practical evolvability limits in principle.
• The success of the experimental setup depends on a sequence of computational runs in order to get an initial pool of programs capable of self-reproducing. The requirement to have a sequence of runs to get to a starting point is not realistic. Nature will not wait or run experiments in parallel in order to select the best and cleanest intermediate results. This is so simply because nature has no decision making or goal setting capabilities. Therefore I think that even assuming a possibility for spontaneous emergence of a replicator, getting an initial pool of replicators that can trigger evolutionary growth of functional complexity is as hard a problem as that the model purports to solve.
• As far as demonstrating that the model can learn, I have less of a concern: Darwinian evolution is able explain to some degree the adaptation of an existing function in the real world. And yet the model still achieves this by intelligent setup/coding. The respective explicit rules to control which individuals of a population to let produce offspring are presented in the paper. The objective function to the organisms need to emulate is given explicitly. Clearly, the more accurately the software organism emulates the given function, the better chance it has to survive and produce offspring, which is fine. In reality though, again, there will be a lot of noise and a lot less sensitivity/efficiency. The sieve of natural selection on an individual level is very coarse: it is either ‘yes’ (reproduction has been achieved) or a ‘no’ (reproduction has not been achieved for whatever reason).
• The author notes time and time again that if computational resources were not limited, the model would not have to exercise fine control over the experimental setup. However, in reality biological resources are limited and therefore we cannot expect the same level of control and sensitivity from natural selection as is assumed or implemented in the model.

Summing this up, the paper exhibits the capabilities of careful experimental design and control. It models artificial selection and learning. It is no surprise: what you built in your model determines what you get out of it. The question is, as usual, to what extent it reflects reality. Design is written all over it.

Further Reading

1. David Abel (2011): The First Gene.
2. Gregory Chaitin (2011): To a Mathematical Theory of Evolution and Biological Creativity.
3. Winston Ewert, William Dembski, Robert J. Marks II (2012): Climbing the Steiner Tree—Sources of Active Information in a Genetic Algorithm for Solving the Euclidean Steiner Tree Problem, In Bio-complexity.org.
4. Winston Ewert, William Dembski, Robert J. Marks II (2013): Active Information in Metabiology, In Bio-complexity.org.

_____________________________

Considerable food for thought, as usual. END