
Here at Uncommon Descent, we never really celebrated Pi Day (March 14) this year because other stuff intervened. But pi is a really important irrational number:
Pi has been calculated to over one trillion digits beyond its decimal point. As an irrational and transcendental number, it will continue infinitely without repetition or pattern. While only a handful of digits are needed for typical calculations, Pi’s infinite nature makes it a fun challenge to memorize, and to computationally calculate more and more digits. More.
Indeed,
In Carl Sagan’s novel Contact, the main character (Ellie Arroway) is told by an alien that certain megastructures in the universe were created by an unknown advanced intelligence that left messages embedded inside transcendental numbers. To check this, Arroway writes a program that computes the digits of π in several bases, and eventually finds that the base 11 representation of π contains a sequence of ones and zeros that, when properly aligned on a page, produce a circular pattern. More.
But some now say that’s wrong. At Science News, Emily Conover argues,
A longtime fixture of high school math classes, pi has inspired books, art (SN Online: 5/4/06) and enthusiasts who memorize it to tens of thousands of decimal places (SN: 4/7/12, p. 12). But some contend that replacing pi with a different mathematical constant could make trigonometry and other math subjects easier to learn. These critics — including myself — advocate for an arguably more elegant number equal to 2π: 6.28318…. Sometimes known as tau, or the symbol τ, the quantity is equal to a circle’s circumference divided by its radius, not its diameter.
This idea is not new. In 2001, mathematician Bob Palais of the University of Utah in Salt Lake City published an article in the Mathematical Intelligencer titled “ π is wrong!” The topic gained more attention in 2010 with The Tau Manifesto, posted online by author and educator Michael Hartl. But the debate tends to reignite every year on March 14, which is celebrated as Pi Day for its digits: 3/14.
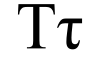
The simplest way to see the failure of pi is to consider angles, which in mathematics are typically measured in radians. Pi is the number of radians in half a circle, not a whole circle. That makes things confusing: For example, the angle at the tip of a slice of pizza — an eighth of a pie — isn’t π/8, but π/4. In contrast, using tau, the pizza-slice angle is simply τ/8. Put another way, tau is the number of radians in a full circle.More.

We recommend digging the big coffee urn out of the back of the closet for this one. Also, cookies and crackers.
See also: Is celeb number pi normal?
Pi: How did mathematics come to be woven into the fabric of reality?
At PBS: Puzzle of mathematics is more complex than we sometimes think
and
Eugene Wigner: Nobel Prize Winner Promotes ID, Ccirca 1960
The dream lives: