Our contributor JB asked to have a conversation on what is important in Mathematics, especially Math education.
I shared some thoughts.
>>Why not, let’s just do that, follow it up and see where it goes?
For instance, I think a key insight is to find a useful, powerful definition of what mathematics is. If we understand what it is we are exploring, it may give us a deeper, richer view on how we may understand and apply it. And for this, I have come to the view that an adaptation of a view I was taught by my very first uni prof is key:
Math is [the study of] the logic of structure and quantity.
That, is, there are two aspects, first, the substance of a certain field of reality: it forms a coherent framework of largely abstract structures and quantities. Coherence, being the gateway to the logic that guides our reasoning, and turns on the premise that realities are so together, thus accurate descriptions of said realities — truths — must equally fit with one another as they must also fit with realities. This means, rational thought is a main tool (and increasing our power of rational thought is a key motive and end) of Mathematics.
Further to this, I see a key application of the logic of being.For, key Mathematical entities, while abstract, are necessary, framework components of any possible world. Which immediately gives them enormous power and depth, as well as being a source of the aesthetic pleasure excited by well done Mathematics — its beauty. Order, intricacy, organising principles reflecting verisimilitude. So, Mathematics can be enriching, enjoyable and en-noble-ing. All of which are highly relevant to education and praxis. Also, the involvement of the appearance and substance of truth (with logical accountability and duties of prudence) brings out an ethical dimension, the other side of axiology.
Mathematics is a value-rich environment.
For example, ponder the compact, powerfully integrative insights locked in Euler’s expression:
0 = 1 + e^i * π
Going beyond, I find that a survey of key structures such as von Neumann’s exploration of the natural counting numbers, N, will help flesh this out, also teaching us the style of creative, insightful exploration that draws out the insightful creativity you are seeking to promote:
{} –> 0
{0} –> 1
{0,1} –> 2
. . . [HUGE!]
{0,1,2, . . . } –> ω
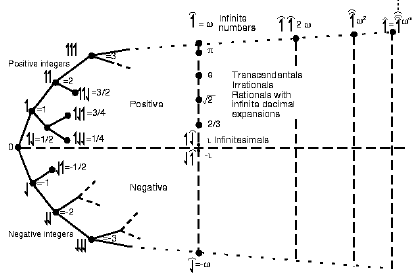
From this we may rapidly access the “mirror-image” additive inverses, thus the Integers Z. Ratios bring us to the rationals, Q. Infinite continued convergent sums of rationals give us the reals, R. Complex numbers C come in as rotating vectors (which then extend to basis vectors, the ijk system, general vectors, quaternions, matrices, tensors thus also groups, rings, fields and algebras). The transfinite ordinals, transfinite hyperreals
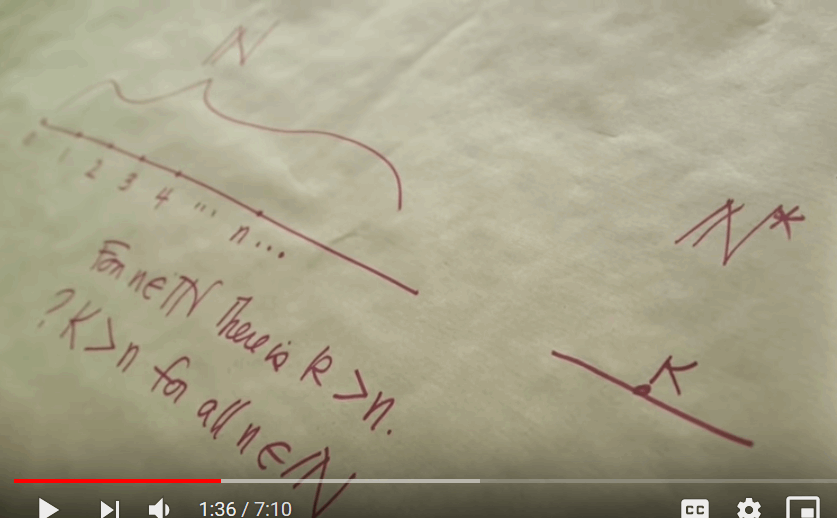
and the catapult through 1/x gets us to infinitesimals, here 1/K.
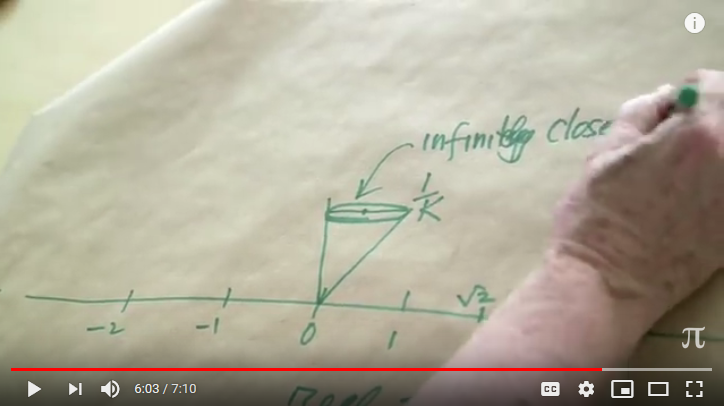
The Surreals come knocking at the door.
Valid infinitesimals give us an insight into Calculus.
With this in hand as a structured survey, all sorts of gateways for exploration are open, including a sound appreciation of sets, mathematical foundations, topology and more. Worthwhile in itself but also obviously relevant to the Calculus you wish to explore. Also, pointing to the world of computing.
We then gain an insight on axiomatisation and how it is subtly shaped by exploration and discovery of key mathematical facts (especially, necessary entities present in the framework of any world). So, we see how axioms may need to be plausible and if well phrased allow us to spin out abstract logic-model worlds that may speak to this and other possible worlds. Where, computing allows us to use machines in that exploration. More broadly, modelling is seen as a powerful but potentially misleading approach. Thus, issues of validation and testing lurk.
We could go on, but I think we see a vision.
While I am at it, Mr Shallit’s sneer falls to the ground, once we see the reality of necessary entities in world frameworks, the relevance of truth, beauty, prudence and more as well as the power of mind to have insight, to intuit, to perceive and to draw insights that transcend the capabilities of inherently blind, dynamic-stochastic, GIGO-limited computational substrates. Reppert, again, draws out the point decisively:
. . . let us suppose that brain state A [–> notice, state of a wetware, electrochemically operated computational substrate], which is token identical to the thought that all men are mortal, and brain state B, which is token identical to the thought that Socrates is a man, together cause the belief [–> concious, perceptual state or disposition] that Socrates is mortal. It isn’t enough for rational inference that these events be those beliefs, it is also necessary that the causal transaction be in virtue of the content of those thoughts . . . [But] if naturalism is true, then the propositional content is irrelevant to the causal transaction that produces the conclusion, and [so]
we do not have a case of rational inference. In rational inference, as Lewis puts it, one thought causes another thought not by being, but by being seen to be, the ground for it. But causal transactions in the brain occur in virtue of the brain’s being in a particular type of state that is relevant to physical causal transactions.
Mathematics is an exercise of the human spirit, which points to that Spirit who is the greatest Mathematician of all. Manifest, in the Mathematical frameworks of our world. A point long since articulated by founders of modern science who saw themselves as seeking to think God’s creative and world-sustaining thoughts after him. >>
Thoughts? END