We live as beings in a world full of other concrete entities, and to do science we must routinely rely on mathematics and so on numbers and other abstract objects. We observe how — as just one example — a fire demonstrates causality (and see that across time causality has been the subject of hot dispute). We note that across science, there are many “effects.”
Such puts the logic of being and causality on the table for discussion as part 4 of this series [ cf. 1, 2, 3] — and yes, again, the question arises: why are these themes not a routine part of our education?
The logic of being (ontology) speaks to possible vs impossible entities, contingent ones and necessary ones. As was tabulated last time:
We see here, that some proposed things such as a square circle are not possible of being: there is no possible world in which they would exist as core characteristics [squarishness vs. circularity] stand in mutual contradiction. This already shows LOI and LNC in action, the principle of distinct identity truly is of central importance. Other things are possible of being (some of which are actual). Where, we may contrast that some must exist as part of the framework for any world to exist (e.g. numbers) — necessary beings. Other things may exist in certain possible worlds but would not exist in others, hence: contingent.
Contingent, on what? Causes.
But first, just what is a possible world? (Is it another name for the multiverse?)
Let us use a surprisingly helpful introductory discussion at Wikipedia — after all,on the principle of charity we must encourage them towards doing a consistently good job:
For each distinct way the world could have been, there is said to be a distinct possible world; the actual world is the one we in fact live in . . . There is a close relation between propositions and possible worlds. We note that every proposition [–> statement that is true or else false] is either true or false at any given possible world; then the modal status of a proposition is understood in terms of the worlds in which it is true and worlds in which it is false. The following are among the assertions we may now usefully make:
- True propositions are those that are true in the actual world (for example: “Richard Nixon became president in 1969”).
- False propositions are those that are false in the actual world (for example: “Ronald Reagan became president in 1969”). (Reagan did not run for president until 1976, and thus couldn’t possibly have been elected.)
- Possible propositions are those that are true in at least one possible world (for example: “Hubert Humphrey became president in 1969”). (Humphrey did run for president in 1968, and thus could have been elected.) This includes propositions which are necessarily true, in the sense below.
- Impossible propositions (or necessarily false propositions) are those that are true in no possible world (for example: “Melissa and Toby are taller than each other at the same time”).
- Necessarily true propositions (often simply called necessary propositions) are those that are true in all possible worlds (for example: “2 + 2 = 4”; “all bachelors are unmarried”).[1]
- Contingent propositions are those that are true in some possible worlds and false in others (for example: “Richard Nixon became president in 1969” is contingently false and “Hubert Humphrey became president in 1969” is contingently true).
The idea of possible worlds is most commonly attributed to Gottfried Leibniz, who spoke of possible worlds as ideas in the mind of God . . . . Scholars have found implicit earlier traces of the idea of possible worlds in the works of René Descartes,[3] a major influence on Leibniz, Al-Ghazali (The Incoherence of the Philosophers), Averroes (The Incoherence of the Incoherence),[4] Fakhr al-Din al-Razi (Matalib al-‘Aliya)[5] and John Duns Scotus.[4] The modern philosophical use of the notion was pioneered by David Lewis and Saul Kripke.
We may summarise, a possible world is a description of the way the — or, a — world might be, inter alia requiring coherence and sufficient completeness for purposes of analysis or action.
For example, in mathematics we routinely construct axiomatic systems that lay out complex abstract model worlds even though, post-Godel we know that no sufficiently complex scheme can be both utterly complete and coherent. Also, that for such schemes we cannot construct an axiomatic system that is demonstrably coherent. (That is, in the end, our confidence in the coherence of our mathematical systems is supported rather than demonstrated; i.e. inductive reasoning is inescapably involved in the practice of mathematics.)
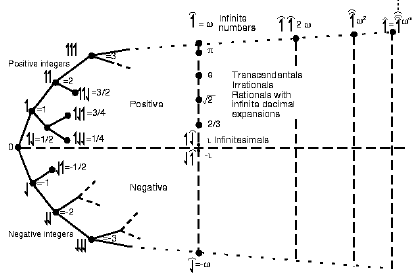
And yes, the utility of Mathematics and its application through computing systems is never far from the surface in our ongoing considerations. Where yes, that means that to some extent we must accept the sufficient reality of a host of abstract, logic-model worlds that we may apply them in our thought and even practical work. Ponder, here, how natural numbers lead to the panoply of transfinite numbers:
We may thus proceed to understand causes and causal factors, first in a fairly narrow sense:
where a contingent entity A would exist in world W1 but would “just” not exist in a closely neighbouring world W2, the difference in circumstances
C(W1 – W2) = f1
allows us to confidently identify f1 as among the relevant causal factors that enable A to be.
Then, we may explore across several neighbouring worlds W2 to Wn, identifying a broader cluster of factors {f1, f2, . . . fn} such that they are each necessary for and are jointly sufficient for A to be.
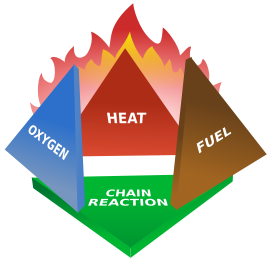
As an example, ponder the extended fire triangle, the fire tetrahedron:
We are also seeing here the significance of experimental studies, observational studies, use-cases, Monte Carlo modelling and statistical investigations, where in effect we set up micro-worlds and study properties as we vary circumstances or ponder natural variations.
In this context, we are already clarifying cause. Wikipedia is again helpful for convenience, broadening our view:
Causality (also referred to as causation,[1] or cause and effect) is what connects one process (the cause) with another process or state (the effect), where the first is partly responsible for the second, and the second is partly dependent on the first. In general, a process has many causes,[2] which are said to be causal factors for it, and all lie in its past (more precise: none lie in its future). An effect can in turn be a cause of, or causal factor for, many other effects, which all lie in its future. Causality is metaphysically prior to notions of time and space.[3][4]
Causality is an abstraction that indicates how the world progresses, so basic a concept that it is more apt as an explanation of other concepts of progression than as something to be explained by others more basic. The concept is like those of agency and efficacy. For this reason, a leap of intuition may be needed to grasp it.[5] Accordingly, causality is implicit in the logic and structure of ordinary language.[6]. . . .
Causes may sometimes be distinguished into two types: necessary and sufficient.[14] A third type of causation, which requires neither necessity nor sufficiency in and of itself, but which contributes to the effect, is called a “contributory cause.”
- Necessary causes
- If x is a necessary cause of y, then the presence of y necessarily implies the prior occurrence of x. The presence of x, however, does not imply that y will occur.[15]
- Sufficient causes
- If x is a sufficient cause of y, then the presence of x necessarily implies the subsequent occurrence of y. However, another cause z may alternatively cause y. Thus the presence of y does not imply the prior occurrence of x.[15]
- Contributory causes
- For some specific effect, in a singular case, a factor that is a contributory cause is one among several co-occurrent causes. It is implicit that all of them are contributory. For the specific effect, in general, there is no implication that a contributory cause is necessary, though it may be so. In general, a factor that is a contributory cause is not sufficient, because it is by definition accompanied by other causes, which would not count as causes if it were sufficient. For the specific effect, a factor that is on some occasions a contributory cause might on some other occasions be sufficient, but on those other occasions it would not be merely contributory.[16]
J. L. Mackie argues that usual talk of “cause” in fact refers to INUS conditions (insufficient but non-redundant parts of a condition which is itself unnecessary but sufficient for the occurrence of the effect).[17] An example is a short circuit as a cause for a house burning down. Consider the collection of events: the short circuit, the proximity of flammable material, and the absence of firefighters. Together these are unnecessary but sufficient to the house’s burning down (since many other collections of events certainly could have led to the house burning down, for example shooting the house with a flamethrower in the presence of oxygen and so forth).
Obviously, a specific contingent circumstance — e.g. the unfortunate burning down of a specific classmate’s house on a particular day in 1976 — had particular distinct causal factors summing up to its specific cause (of interest to the Insurance company) etc. However, once we loosen to a house burning down, we see that we can properly take cause in a looser sense (e.g. of interest to those writing fire safety regulations). This them makes good sense of sufficient but not necessary causal factors as for instance Mackie raised.
Obviously, for an event E, all necessary causal factors (in this looser sense) must be present, as knocking out any one will block it. Likewise, a sufficient cluster must be present which may include broader contributory factors. For example, while a court building here could have caught fire through a short, fire fighters and the police were very interested to observe evidence of accelerants. Not all fires are arson, but some are.
All of this of course feeds onwards into another categorisation of causal factors: mechanical necessity, chance/random factors, intelligently directed contingency. But, that discussion is for another day, save, that we can lay out an explanatory factor flowchart:
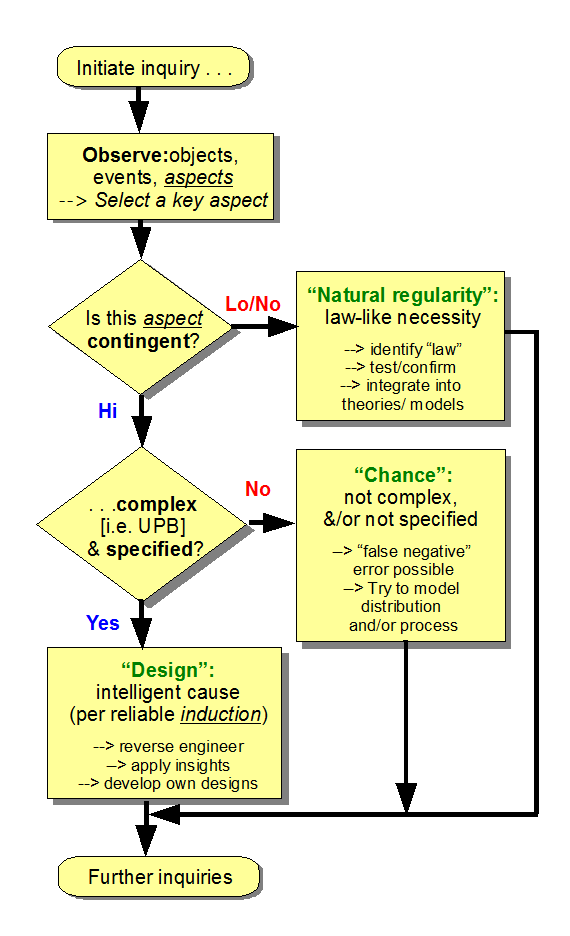
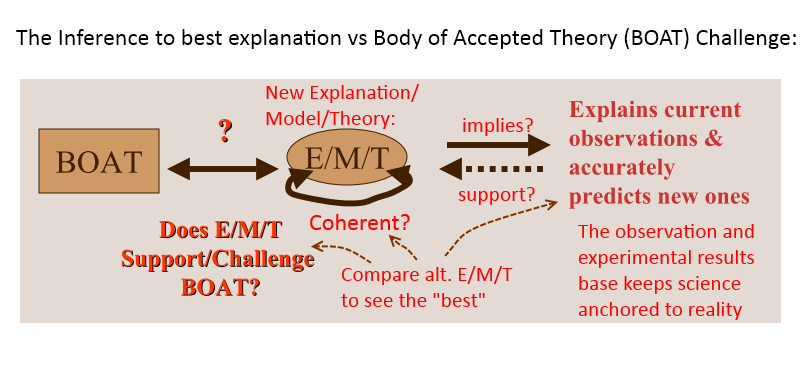
. . . and may ponder competing explanations through abductive inference to best explanation so far:
But, are all entities contingent? No. For, as numbers already indicate, some entities are necessary for any world to exist, as they are inherently part of the framework. To see that, we call on the resources of the principle of distinct identity. Notice, above, we contrasted W1 and W2 etc, drawing out differences even between neighbouring possible worlds. Thus, each world Wk has its own distinct identity and we may freely identify some A such that Wk = (A|~A}. Already we see by partition, twoness. From twoness we infer to one-ness and nullity as emptiness {}. Then, following von Neumann:
{} –> 0
{0} –> 1
{0,1} –> 2
. . .
[Thence, the onward panoply of the transfinites.]
Etc.
Numbers, thus the logic of structure and quantity — the substance of Mathematics, are inherent to the framework of any possible world. This already implies reality in some sense of abstract being. And it further seems that the abstract model worlds of core Mathematics can be sub-worlds integrated with physical ones. Peculiar indeed.
Numbers, we have seen, are necessary beings.
Such NB’s (as opposed to contingent ones, CB’s) have peculiar properties. For one, no Wk is possible in which NB’s do not exist. Try to ponder a world where 2-ness does not exist, or begins to exist or ceases from being. Impossible. Thus, we see a constraint that highlights worlds that are impossible of being. And, a serious candidate NB will therefore be either impossible of being (square circle logic) or it will be present in any actualised Wk. One implication is, that a world is — manifestly so, implies that all truly necessary beings eternally are.
Where of course, the God of Ethical Theism is a serious candidate necessary being. He is either impossible of being or actual. And yes those who claim to know or to practically know he does not exist in actuality have taken up a huge burden of proof. One, I daresay, has never been met. (If you doubt, just fill in one of those pesky UD blanks: ______ Where, for example, post Plantinga, the problem of evil is effectively dead.)
All of this points onward to a further thorny issue: intelligibility (at least to God! and partly, to us!) of the world.
That is, some form or other of the principle of sufficient reason. I here put up a weak form sufficient to pursue logic of being:
[PSR, weak (investigatory) form:] Of any particular thing A that is
[. . . or (ii) is possible, or even (iii) is impossible],
we may ask, why it is
[. . . or (ii’) why it is possible, or (iii’) why it is impossible],
and we may expect — or at least hope — to find a reasonable answer.
Of course, for any given case, X, we may simply directly proceed to ask why is X so, or why is X possible or why is X impossible, and seek a reasonable answer. So, the weak form as it stands is unobjectionable. It is also central to science and to the project of being rational, responsible creatures.
Linked, we may ponder a claim some have advanced, that our world is just one stage in an ongoing infinite in the past and potentially infinite in the future, chain of successive, causally-temporally linked stages, back to the singularity and beyond without limit:
. . . s-n, s- (n-1), . . . s-2, s-1, NOW, s+1, s+2 . . .
This has been repeatedly debated here at UD, and I continue to hold that the proposed past infinity is incoherent as it has no basis to arrive at now in finite successive stages. Others have claimed differently. I doubt such claims as actual stepwise succession in finite steps cannot ever span a transfinite range.
So, we here see causality and intelligibility of being as key first principles of rationality. END
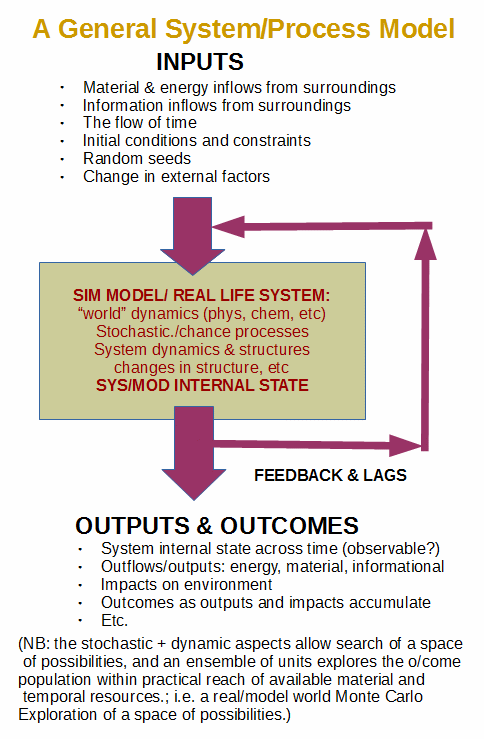
PS: As issues on dynamics and trajectories have been raised, here is a basic system diagram:
This gives a context to consider initial state, traversal across phase space and impact of intervening forces, noise etc.