Daily Mail reports on a class assignment for seven year olds that happened to be set for the daughter of a Mathematics Lecturer at Oxford.
Maths lecturer is left baffled by his seven-year-old daughter’s geometry homework and turns to Twitter for help – so can YOU work out if it’s true or false?
Dr Kit Yates shares his seven-year-old daughter’s maths homework to Twitter
The question asked students whether a semi-circle had ‘two right angles’ or not
The maths lecturer, from Oxford, admitted that he was stumped by the problem
People were left baffled by the question and came up with conflicting answers
By Kate Dennett For Mailonline
Published: 17:40 GMT, 25 February 2021 | Updated: 17:40 GMT, 25 February 2021
Here is the question and the “expected” seven year old School Math answer:
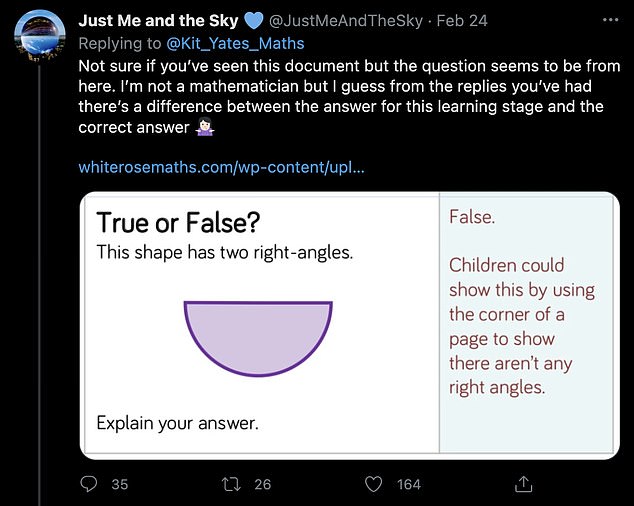
Why would a PhD level Maths Lecturer disagree? Indeed, why would he suggest — and this is where it gets interesting for us here at UD — “there was a strong case for claiming that the answer was ‘true’ as well as ‘false’“?
Sounds familiar?
Obviously, a Math Lecturer — I switch to the American style abbreviation — will be familiar with the world of the infinitesimal. So, he would be aware that at the point of intersection of diameter and circumference, there is a required right angle to the tangent and that at that point curve and tangent coincide . . . the tangent and the curve share the same slope at that point, but not at any identifiable real value on the circumference beyond — thus, distinct from — that point.
Arguably, for an infinitesimal spread about the point where the tangent touches the curve and the diameter cuts it, we have a straight line segment c_0 +/- dc in the circumference but at right angles to the diameter. That is, the hyperreals are peeking in and giving us a language to constructively talk about structures and quantities.
Let’s cross check, through Wikipedia:
In geometry, a polygon (/ˈpɒlɪɡɒn/) is a plane figure that is described by a finite number of straight line segments connected to form a closed polygonal chain or polygonal circuit. The solid plane region, the bounding circuit, or the two together, may be called a polygon.
The segments of a polygonal circuit are called its edges or sides, and the points where two edges meet are the polygon’s vertices (singular: vertex) or corners. The interior of a solid polygon is sometimes called its body. An n-gon is a polygon with n sides; for example, a triangle is a 3-gon.
Notice, the requirement, “finite number of straight line segments”? Other common sources will omit finiteness, and it is commonly recognised that a circle is a beyond finite case of a regular n-gon. So, we have reasonable grounds for referring to infinitesimal line segments and removing the finitude. For example, that is one way to approach the question, what is the area of a circle.
I should note that an infinitesimal value can be seen as a number say h near to 0 in the number line, closer to 0 than any 1/n, where n is a finite counting number. (This opens up also the concept of transfinite hyperreals. That is h = 1/H, a number such that H > n for any finite counting number.)
Shifting to Coordinate Geometry, let’s put our circle at the origin, O, and give it radius r:
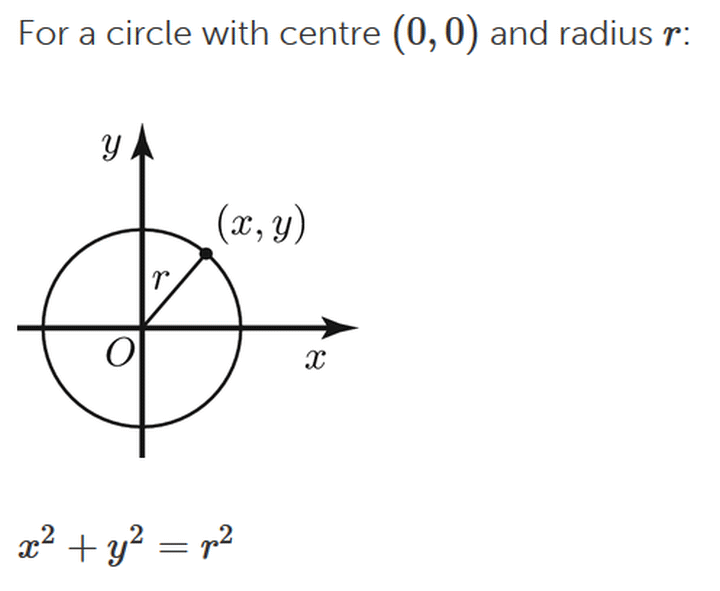
With these ideas in hand, we can see that by using infinitesimals, a circle is a limiting case of a regular polygon, but the length of sides is too short to be captured by any distinct point on the circumference c_1 at (x1,y1) distinctly removed from C_0, at (x0,y0) such that x1 – x0 is a real value, and the same for y1 – y0. (That is, we here mark a distinction between the infinitesimally altered x0 + dx or the similarly altered y0 + dy and any neighbouring x1 and y1, constrained to be strictly real.)
This allows us to seemingly have our cake and eat it.
That is, no distinctly removed point c1 with strictly real coordinates different from c0 will lie on the tangent to the circle at c0 at the point where the diameter cuts the circle. But at the same time we can speak reasonably of points along a short line segment at c0, that is straight but in the circumference, as the points in question c0 + dc, are infinitesimally removed from c0. Where, dc^2 = dx^2 + dy^2.
That is, further, we are looking at an infinitesimal right angle triangle with the hypoteneuse dc being on the tangent line for the circle at c0.
If we can swallow this camel, then we have an answer, yes there is a right angle at the intersections of diameter with circumference, and yes the circle is bounded by a closed curve where any distinct c_1 at (x1,y1) that is such that x1 and y1 are strictly real, will fall away from the tangent at c_0.
Is such reasonable?
Well, let us see how we arrived at the differential coefficient dy/dx, as an expression of the slope of y = f(x) at some point on a curved line, through the slope of the tangent-limit to the slopes of the secants:
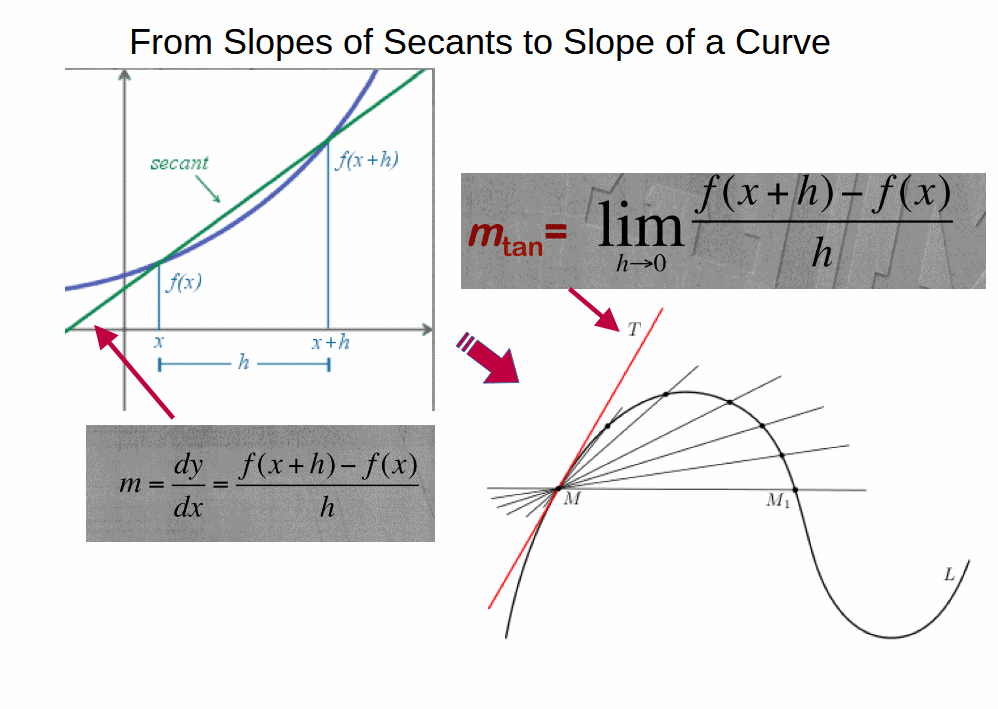
Here, we see how the slopes of secants, in the limit, become the slope of the tangent at M, as h tends to 0, i.e. becomes an infinitesimal.
Now, let us ponder the curvature of a continuous, differentiable line:
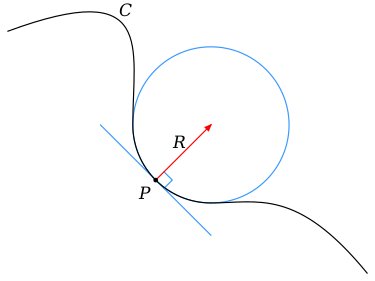
Here, curvature K = 1/R, R the radius of curvature. Observe that the tangent line is perpendicular to the curve and its osculating circle, which near P is coincident with the curve. All of this begs for interpretation on infinitesimals. BTW, for a straight line, the radius of curvature is infinite, yielding a curvature of 0.
With these in mind, we can see that no, this is not a superposition of two contradictory states but a case that is surprisingly relevant, regarding the value of the infinitesimal perspective.
Now, where does this all lead? Interesting places . . . END