One of the more astonishing points of debate that has come out at UD is that at least some defenders of the evolutionary materialistic view are prepared to argue for or assume as default that we have had a beginningless past for the physical world. This has come up several times in recent years and was again discussed last week.
I will share my take-away conclusion so far.
But first, why are such willing to put up such a spectacularly untestable, unobservable claim?
Because, we first know that non-being has no causal powers so if there were ever utter nothing, such would forever obtain. That a world manifestly is implies that SOMETHING always was. The question is what, given that our observed cosmos is a temporal-causal entity and credibly began at the singularity, perhaps 13.85 BYA:
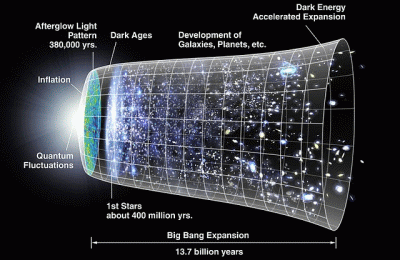
That cannot be a beginning from nothing, so the issue is, what went on before?
Thus, a causal form of the Agrippa trilemma. Circular cause at the world-root would imply the non-existent future stage causing its antecedent past, absurd. There is an objection from such quarters to the concept of a finitely remote beginning, rooted in a necessary being as what always was. So, some are left to defend the claim that an infinite onward past is coherent, feasible and perhaps plausible. And, in that defence, the claim is made, no there are no past stages of the world that are actually transfinitely remote, just that there is an endless onward succession of prior states [each finitely remote] so that overall for any given past stage p or r, there are further states beyond it no matter how large the stage-count from now to p or r is.
Such an argument makes reference to this definition of infinity, from Merriam-Webster, discussed at 68 in last week’s thread:
>>Merriam-Webster:
Definition of infinite
1 : extending indefinitely : endless
infinite space
2 : immeasurably or inconceivably great or extensive : inexhaustible
infinite patience
3 : subject to no limitation or external determination
4 a : extending beyond, lying beyond, or being greater than any preassigned finite value however large
infinite number of positive numbers
b : extending to infinity
infinite plane surface
c : characterized by an infinite number of elements or terms
an infinite set
an infinite series
[KF:] It seems the key point of meaningfulness is in a blend of 1, 2 and 4a:
1 : extending indefinitely : endless . . . . 2 : immeasurably or inconceivably great or extensive : inexhaustible . . . . 4 a : extending beyond, lying beyond, or being greater than any preassigned finite value however large
[KF:] Notice, the key operative terms: “endless . . . . inexhaustible . . . . extending beyond, lying beyond, or being greater than any preassigned finite value however large.”>>
I have responded, and here is my conclusion at the moment:
KF, 98 :>>Perhaps, it is time to draw up some conclusions, and make statements of appreciation.
First, deep appreciation must be extended to DS, JDK and other interlocutors. DS has been particularly helpful over two years, indeed it is he who drew my attention to the surreals as a means of seeing the grand picture of numbers great and small. Despite disagreements and divergence of views, that has been important.
Now, what of the state on the merits? Of what significance is all of this stuff on abstruse topics linked to numbers?
Perhaps, we can start with an extended form of the definition of Mathematics I was taught in M100 by a famous prof: mathematics is [the study of] the logic of structure and quantity.
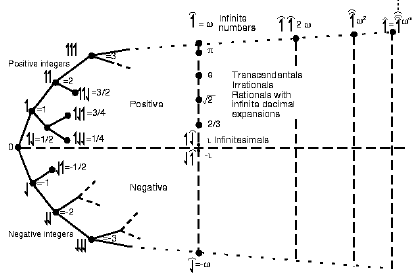
So, if we are to properly, truthfully understand the world, we should study that logic, the issues of structure and the nature of quantities involved with “numbers great and small.” The surreals are important, and the hyperreals (thus also, infinitesimals).
That search for truthful, adequate understanding has been my main motive, a motive that I recommend to one and all.
Closely linked is the educational issue: how can we bring more and more to a better understanding of these things? (Let me disclose that a bit less than two years ago I was a guest on a local radio show on education matters, and these general issues were focal. I found it particularly interesting to see the public’s reaction to my tying-in music with Mathematics and Physics. That may be a hint on reaching out to people where they are.)
Next, I find that the concept of the hyperreals is truly significant. Especially, by way of the thought-exercise of allowing a point of interest to follow the locus of sinking from 1 towards 0 along the open continuum- interval (0,1] and taking the reciprocal, 1/x.
This generates the line of the reals beyond 1 as a continuum also. Along that line we see 1/1, 1/2, 1/3 etc generating the marker-points that come up from von Neumann-style succession or successive addition by 1’s. Let’s use von Neumann as his approach shows how abstract and powerful numbers are in light of (i/l/o) set concepts. To do so, start with the empty set and denote what are called order types, extending to omega, which for convenience we can represent as w:
{} –> 0
{0} –> 1
{0,1} –> 2
{0,1,2} –> 3
. . .
{0,1,2,3 . . . } –> wWe see here how the set that collects nothing has cardinality (“size”) zero, and let that define our start point for quantity. Zero is an entity with distinct identity. It is something by contrast with nothing — and yes the triple first principles of right reason are embedded here: world = {A|~A} where A is itself i/l/o core characteristics that mark its distinct identity and ~A is another entity distinct from A, the rest of the world and what is in it. So too we may see the corollaries, LNC and LOI: no x in World is A AND ~A, any x in World will be A X-OR ~A, in one or the other, not both, not “nowhere.”
But this already gives us one, and two.
Further distinct identities follow in a chain, 3, 4, etc. The three-dot ellipsis — how I wish it were standard to use four dots for limitless extension — then indicates an endless ordered succession. This is complementary to
1 + 1 + 1 + . . .
We then find that we have countable numbers in endless succession, that endlessness allowing us to recognise a new type of quantity, the order type of the natural counting numbers, omega [here, w].
The set of the naturals is deemed infinite, by way of that ongoing endlessness of succession. In this context, w is the first transfinite ordinal number; denoting the order-type of the naturals.
Back to the 1/x on the continuous, open interval (0,1]. And by multiplying through by -1, we have the negative number line.
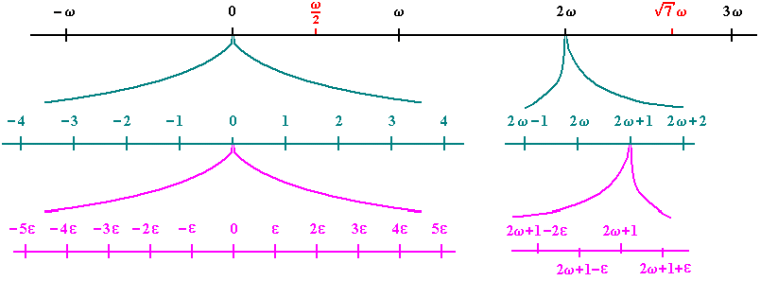
Here, we can see the filling-in between the naturals [and integers], which decimal representation allows us to complete by using ever finer decimal fractions without limit. This, we also see in the inner branches of the surreals diagram. The line of the reals is the continuum towards w. The idea of the surreals is to squeeze in on specific values from above and below like the closing jaws of a vice.
Now, we know that 1/x, x = 0 is forbidden, as there are all sorts of resulting problems. However, on the brink of 0, very interesting things happen. Let e be such that e^2 ~ 0, a yardstick infinitesimal. Where [2e]^2 ~ 4 x 0 = 0. Now we hold by selection of the “appropriate” value of e:
1/e = w/1
so, too
1/2e = 1/2 x 1/e = w/2
We unify, and extend the number line to the hyperreals. This goes beyond the somewhat unsatisfactory picture given by whole number succession, that w is the order type of the naturals.
Of course, the point is that (0,1] is a continuum, so the numbers line is here unified for the very small and the very large. With, the span beyond w also a continuum as we can keep sliding in in the all but zero range without actually hitting 0.
And we now use the property that e is not a FIRST infinitesimal but a YARDSTICK one to see that the range of numbers naturally assigns to something like w/2 and the like. As a consequence we can make sense of the idea that infinitesimals are smaller than any real, and hyperreals are larger than any real. That is, the ellipsis marks that veiled grey zone in which finite results yield to infinitesimals on the brink of 0, that are tied by the catapult hyperbolic function 1/x to hyperreals beyond any finite real. Where, of course, the natural counting numbers are the whole number mileposts along the way.
We have built up a significant set of concepts which allow us to better address structures and quantities.
Let me add that if we look at planar space and locate the numbers line as the o-x axis, we may then suggest an anticlockwise, right angle rotating operator i such that i*x gives us a perpendicular axis. Apply i twice:
i*i*x = – x
We just defined i as the square root of -1. We also define a quantification of planar space, where the orthogonal [= perpendicular] o-y axis is the i*x axis. This actually gives us a way to define a new class of numbers, complex numbers:
z = a + i*b
By watching our i’s carefully, we now have a way to handle quantities with both magnitude and direction, algebraically. Complex numbers are one algebraic way to handle vectors, with powerful results all over mathematics. And, we may extend to three-axis vectors using the ijk unit vectors scheme. (And BTW, that is one reason Physicists use j for the sqrt – 1, it helps further unify.)
Infinitesimals, of course are one gateway to calculus. In effect every real number is surrounded by a cloud of neighbouring infinitesimals. This gives a fairly straightforward interpretation to many Calculus operations. The C19 delta-epsilon, limits based approach came up to handle issues triggered by naive use of infinitesimals. Just as, naive set theory has had to be refined. In pure Mathematics, much effort has to be put in in working around truly pathological cases.
I think this picture is a useful exercise for its own sake.
It also helps us to clarify what is at stake in discussing what it means to claim that the [quasi-]physical cosmos has had a beginningless, thus infinite, past. That is, the logic of structure and quantity includes the bridge between the finite and the transfinite, which then applies to the question of a world or a world-root that was always there. The logic of being applied to the being and origin of the physical cosmos, is not without reference to the logic of structure and quantity.
Truth is unified, coherent, as all truths must hold together in a world, and if truth A is the denial of truth B that would not obtain.
Now, the source of our world cannot be utter non-being, as such hath not causal powers. Were there ever utter nothing, such would forever obtain. That a world in which we exist as self-aware, conscious en-conscienced, thinking and understanding creatures self-evidently exists as a going concern, SOMETHING always was. The debate in cosmology is the nature of that world-source.
Further to this, the world is spatial and temporal. Moving beyond Zeno’s paradoxes, we can consider the going-concern world as a structured set succession of finite-duration stages — years, for convenience — down to now, S:
S = { . . . –> p –> p+1 . . . –> 0}
Now is ever moving on from one stage to the next, there is a cumulative, causal-temporal order to the physical world.
Now, our observed world is generally held to have come from a “singularity” some 13.85 BYA, the big bang. A finitely remote origin. But, whence the “bang”? Not from utter non-being. Down that road lies a great discussion populated with fluctuating quantum foams, oscillating worlds, budding sub-cosmi, multiverses, strings and branes etc.
However, we may look from a different angle, Agrippa’s trilemma in causal form on going concern world-source:
[a] finitely remote cause by a necessary being world-root,
[b] infinite causal regress of a beginningless [quasi-]physical wider cosmos,
[c] self-causation in a circle at the root.
We can address c first. If there is circular cause, the non-existent future reaches back to cause its past. This boils down to appeal to cause from non-being. Ruled out.
Option a would work, but is often deprecated as appeal to the unobserved, god of gaps, violation of Occam’s razor, etc. However, the issue is, there is of necessity a root that was always there, we do not pull a world out of a non-existent hat.
As for necessary being, the von Neumann chain and the linked logic show that distinct identity thus two-ness [and beyond the panoply of numbers] will always be there. It is possible, as actual. It is there in any possible world, not least because such a possible world holds its own distinct identity. It never began, it cannot cease from being, it is independent of external enabling causal factors. Necessary being, though strange to our thoughts perhaps, is real.
Option c is favoured by many and has been the occasion for several exchanges along lines much as above.
The pivotal issue, of course, is what lurks in that grey area indicated by the ellipsis. The answer is, the bridge to the transfinite.
So, if we consider the proposed beginningless causal-temporal world, we find the idea that first, the past is actual. That is, any past stage R was once the present, a duration – R_t from now, where now is regarded as 0 for convenience and past times are negative:
Duration since R:
D(R) = 0 – R_t = – R_t
The beginningless past claim, then, is that for any specific R, and for any specific n in the naturals (N), there will be actual onward past times that are before R, beyond any specific n. That is, limitless in the past beyond R.
Such is a strong claim indeed.
Does it imply that there are past times that are remote of order w?
I have symbolised that situation as in effect S:
{ . . . q –> q+1 –> . . . p-1 –> p –> p+1 . . . 2, 1, 0}
where the first and second ellipses are transfinite in span.
This expansion of the ellipsis beyond p has been denied:
{ . . . q –> q+1 –> . . . p-1 –> p –> p+1 . . . 2, 1, 0}
In particular, it has been held that all specific vales leftwards [L-wards, contrast R-wards] of p are also finite but extend without limit.
Part of the reason, doubtless, is that a stepwise finite stage cumulative process cannot traverse a transfinite span. For, if it attains any stage k, we can treat k as if it were the beginning again, k, k+1, k+2 etc and 1:1 match process from the original point regarded as 0. That is part of how we understand the process to be transfinite, beyond limit. And with that stricture, no stepwise process will span an actual infinite traverse, So, it is held, there is no actually transfinitely remote actual past point. The infinity lies in the beginninglessness, beyond limits nature of the succession. Where all is neatly coherent, it is not impossible and cannot be dismissed; implying, adequate and sufficiently satisfactory explanation.
Another claim was that q smuggles in a beginning. Obviously, no, it too is preceded by a L-ward ellipsis.
So, is that where we must stand? I don’t think so.
The problem lurks in the grey area, we are obviously embarked in the zone where the finite transitions to the transfinite. Where, the implicit pivot of the argument is non-traversal of the transfinite. But, a successive stepwise process that extends L-wards beyond any n in N is clearly of transfinite character. Just what is it that lies “beyond any n in N” other than the transfinite? But if we focus on finitude of specific numbers R or n, we may miss that character.
So, it seems that whether or not one will accept that there is an implied actual past time of character q, one implies successive, stepwise traversal of a transfinite span.
Where, such a stepwise process does not have that power. That is a point by W L Craig, too, as summarised by SEP (it is not just an idiosyncratic, readily dismissed notion):
5 An actual infinite cannot exist.
[He has many reasons for that, which are often hotly contended but on the whole I think he has a serious point . . . at minimum he has shown that modern atheism effectively is reduced to a highly contentious assumption about the past, which is very different from its boast that it can be seen as a default for the intelligent person]
6 A beginningless temporal series of events is an actual infinite.
[Note this]
7 Therefore, a beginningless temporal series of events cannot exist.
Since (7) follows validly, if (5) and (6) are true the argument is sound . . . .
>> 6.3 Successive Addition Cannot Form an Actual Infinite
Craig’s second argument addresses this very point.
8 The temporal series of events is a collection formed by successive addition.
9 A collection formed by successive synthesis is not an actual infinite.
10 Therefore, the temporal series of events cannot be an actual infinite (Craig 1979: 103).
The collection of historical events is formed by successively adding events, one following another. The events are not temporally simultaneous but occur over a period of time as the series continues to acquire new members. Even if an actual infinite were possible, it could not be realized by successive addition; in adding to the series, no matter how much this is done, even to infinity, the series remains finite and only potentially infinite. One can neither count to nor traverse the infinite [–> in such a stepwise fashion] (Craig and Sinclair 2009: 118).
It might be objected that this sounds very much like Zeno’s paradoxes that prohibit Achilles or anyone from either beginning to cross an area or succeeding in doing so. But, notes Craig, significant disanalogies disallow this conclusion. For one, Zeno’s argument rests on progressively-narrowing, unequal distances that sum to a finite distance, whereas in traversing the past the equal distances continue to the infinity of the future.
[–> relative to the distant past in view. This is also the context in which I have consistently spoken of finite stage causally successive stages]
Second, Zeno’s distances are potential because of divisibility, whereas the distances from the past are actual distances or times to be traversed.
Beyond, lurks time’s arrow; entropy. Part of the driving-force of causal-temporal succession is that there are rich concentrations of energy that support processes of change. But that means the sources are gradually degraded and as they are finite, we look at what has been called heat death. Such is a condition where the degradation of energy has attained a point where the energy sources — stars are especially in view — have been used up.
That we are not in this degrades state implies, then, a finite date; at least i/l/o understanding the cosmos as a whole as an isolated system. Of course, it was suggested above, that perhaps there is an external non-physical source able to sustain the world “forever” through adding fresh energy. This is in effect continuous creation by an entity that would recognisably be God.
And that is a shocker for confident evolutionary materialism advocates.
Is there a physically beginningless world coeval with God who sustains it from without?
To such a model, we can note that one may speculate as one pleases, the evidence we can observe prunes speculations by highlighting evidence of a beginning rooted in back-projection of an expanding world with background microwave energy consistent with the about 14 BY origin. Likewise, we would expect to see a huge number of degraded stars, including cooled down white dwarfs. These are not seen with any numbers to support a beginningless world working much as what we observe.
In all of this light, the best explanation on the table is finitely remote origin of our world, tracing to a necessary being world-root.
Beyond, we may discuss implications of such a world having in it conscious, minded creatures able to seek out explanations of an intelligible world, who find ourselves under moral government.
Such is an onward exercise and the road to it lies through the AI issue, including the further exploration of memristors.
DV, another day.>>
Okay, that’s where I think things are just now. Thoughts? END