The hyperreals are an extension of the real number line that brings to bear a reciprocal relationship between the very large and the very small. By so introducing extensions to the real number continuum, it forms a base for an infinitesimals approach to the calculus and makes sense of a lot of the tricks used by early pioneers of Calculus from Leibniz and Newton to Euler and beyond. (Though, it is clear in retrospect that they missed a lot of the pathologies that are now part of the far more cautious approaches of today.)
And yes, here is a case where Wikipedia does some good (likely, in a context where there are few basement trolls capable of making a mess):
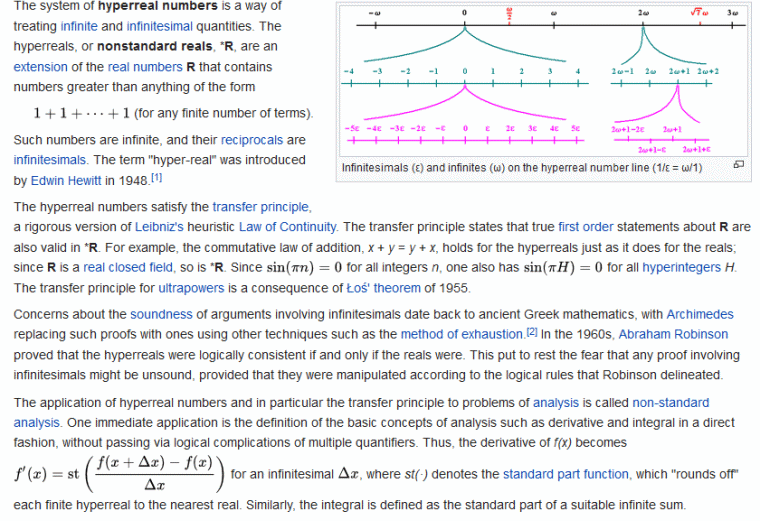
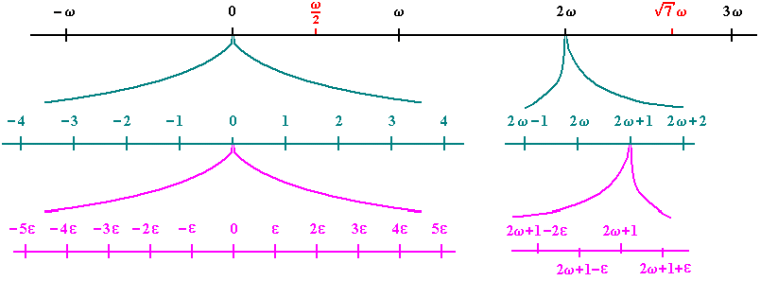
Let’s zoom in on the graphic, which illustrates the “hyperreal microscope” of *R:
Let us note the definitional relationship between the infinitesimal and the hyper-large:
1/ε = ω/1
Where also, a common principle used is that ε is so small that ε^2 = 0. Where, to see what that is suggesting consider that (1/10)^2 = 1/100, and (1/10^50)^2 = (1/10^100), i.e. squaring drastically reduces the scale of a very small number.
This is all quite interesting, and has been used to rehabilitate some of Euler’s work, e.g. here.
(This is also quite relevant to some of the “Math tricks” used by Physicists and Engineers. The reference to the hyperreals may be a way to rehabilitate some seemingly dubious tricks.)
The principle that ω is a number greater than any finite sum 1 + 1 + 1 + . . . + 1 implies that it is of order type at least comparable to the first transfinite ordinal. The inclusion of the further numbers such as ω/2 indicates a reference to the surreals, and something like root-7 times ω indicates an onward transfinite continuum. I do not at this juncture specifically identify this ω with the familiar first transfinite. (Perhaps someone cares to clarify?)
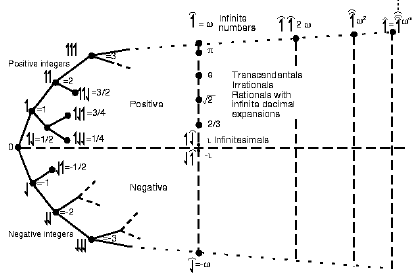
So, we may at least highlight the surreals, where the vertical bars indicate continua — note the place for “infinitesimals”:
All of this is interesting in itself, as numbers are the tools of ever so much analysis and we here enrich appreciation of our favourite tool-box. (I confess, this weekend was more spent with dynamic-stochastic general equilibria, linked rational expectations, questions on modern theories of growth and human capital, etc. All, with Garrison’s Austrian approach to macroeconomics lurking, and blending in issues of saturation and stagnation at points along the PPF as well as what happens to shocked economies with low investor confidence . . . as in, 20+ years on from devastating volcanic eruptions. This stuff was the oh, what about light exploration as a relief.)
But all of this converges on something which has come up for strong, sustained exchanges several times here at UD. Namely, the suggestion of an actual infinite causal-temporal past of the [wider?] cosmos. For, if ω is such that no finite succession from 0, 1, 2 via 1 + 1 + 1 . . . + 1 can reach it, then counting down — notice, the ladder-like succession of steps (and how the surreals extend this to construct continua and to go into transfinite ordinals) — from it in finite succession [or by symmetry counting algebraically upwards from – ω] may reach to something like ω/2 [or – ω/2] but it will be futile for getting to a finite reach of a zero-point.
In short, we can see here a reason to hold that there was no actually transfinite causal-temporal succession of states that have managed to reach the present. Nor will it do to posit that at any given past time p that can finitely succeed to now, infinity past was already traversed. That begs the question of HOW.
This also surfaces a logic of being point.
Namely, that non-being has no causal powers, so that if ever there were utter nothing, such would have forever obtained. Thus also, circular causation is forbidden as this would imply that the not yet existent acted as a cause. Thus, we either have an infinite succession of contingent beings as the world-root or else there is a necessary being at world root. That is, an entity such that it is utterly unlike a fire, which has several required external, enabling “on/off” causal factors for it to begin or be sustained:
Where this goes, is that a necessary being is framework for any possible world to exist. So, in any world, it would be. It neither began nor can it cease from being. For instance, in reality we may consider a world W, which must have a distinct identity. So, too, we may consider some distinct thing in W, A that contributes to its identity. Then, we may look at W = {A|~A}. This shows two unities, i.e. two-ness. No world is possible without two-ness, and beyond, the panoply of numbers.
This is what gives bite to Berlinsky’s remark that was just raised here at UD:
>>There is no argument against religion that is not also an argument against mathematics . . . .
Mathematicians are capable of grasping a world of objects that lies beyond space and time ….
… Come again …
DB: No need to come again: I got to where I was going the first time. The number four, after all, did not come into existence at a particular time, and it is not going to go out of existence at another time. It is neither here nor there. Nonetheless we are in some sense able to grasp the number by a faculty of our minds. Mathematical intuition is utterly mysterious. So for that matter is the fact that mathematical objects such as a Lie Group or a differentiable manifold have the power to interact with elementary particles or accelerating forces. But these are precisely the claims that theologians have always made as well – that human beings are capable by an exercise of their devotional abilities to come to some understanding of the deity; and the deity, although beyond space and time, is capable of interacting with material objects.
… And this is something that you, a secular Jew, believe? …
DB: What a question! . . . I have no religious convictions and no religious beliefs. What I do believe is that theology is no more an impossible achievement than mathematics. The same rational standards apply. Does the system make sense; does it explain something? Are there deep principles at work. Is it productive? >>
So, now, we see from the hyperreals augmented by ideas of causal-temporal succession, that it is hard to defend the notion of a transfinite actual past of contingent beings leading up to now. This points to there being an actual beginning of the world and that this traces to a finitely remote necessary being world root.
That’s enough for a UD Sunday reflection! END
PS: As it is being claimed or implied that no serious thinker thinks like that, I add a clip, just for record: