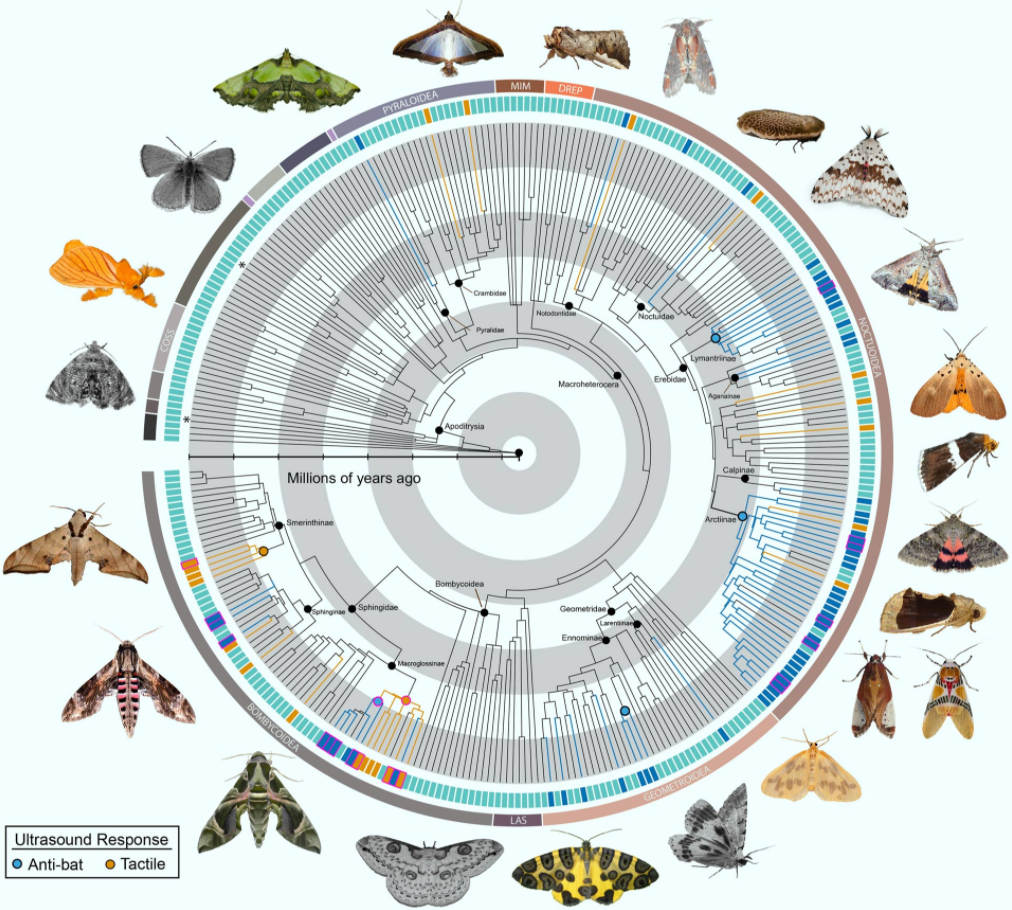
Scientists from Boise State University and elsewhere have tested 252 genera from most families of large-bodied moths. Their results show that ultrasound-producing moths are far more widespread than previously thought, adding three new sound-producing organs, eight new subfamilies and potentially thousands of species to the roster.
Bats pierce the shadows with ultrasonic pulses that enable them to construct an auditory map of their surroundings, which is bad news for moths, one of their favorite foods.
However, not all moths are defenseless prey. Some emit ultrasonic signals of their own that startle bats into breaking off pursuit.
Many moths that contain bitter toxins avoid capture altogether by producing distinct ultrasounds that alert bats to their foul taste. Others conceal themselves in a shroud of sonar-jamming static that makes them hard to find with bat echolocation.
While effective, these types of auditory defense mechanisms in moths are considered relatively rare, known only in tiger moths, hawk moths and a single species of geometrid moth.
“It’s not just tiger moths and hawk moths that are doing this,” said Dr. Akito Kawahara, a researcher at the Florida Museum of Natural History.
“There are tons of moths that create ultrasonic sounds, and we hardly know anything about them.”
In the same way that non-toxic butterflies mimic the colors and wing patterns of less savory species, moths that lack the benefit of built-in toxins can copy the pitch and timbre of genuinely unappetizing relatives.
These ultrasonic warning systems seem so useful for evading bats that they’ve evolved independently in moths on multiple separate occasions.
In each case, moths transformed a different part of their bodies into finely tuned organic instruments.
[I’ve put these quotes from the article in bold to highlight the juxtaposition of “evolved independently” and “finely tuned organic instruments.” Fine-tuning is, of course, often associated with intelligent design, rather than unguided natural processes.]
See the full article in Sci-News.