ID proponents and creationists should not use the 2nd Law of Thermodynamics to support ID. Appropriate for Independence Day in the USA is my declaration of independence and disavowal of 2nd Law arguments in support of ID and creation theory. Any student of statistical mechanics and thermodynamics will likely find Granville Sewell’s argument and similar arguments not consistent with textbook understanding of these subjects, and wrong on many levels. With regrets for my dissent to my colleagues (like my colleague Granville Sewell) and friends in the ID and creationist communities, I offer this essay. I do so because to avoid saying anything would be a disservice to the ID and creationist community of which I am a part.
[Granville Sewell responds to Sal Cordova here. ]
I’ve said it before, and I’ll say it again, I don’t think Granville Sewell 2nd law arguments are correct. An author of the founding book of ID, Mystery of Life’s Origin, agrees with me:
“Strictly speaking, the earth is an open system, and thus the Second Law of Thermodynamics cannot be used to preclude a naturalistic origin of life.”
Walter Bradley, Thermodynamics and the Origin of Life
To begin, it must be noted there are several versions of the 2nd Law. The versions are a consequence of the evolution and usage of theories of thermodynamics from classical thermodyanmics to modern statistical mechanics. Here are textbook definitions of the 2nd Law of Thermodynamics, starting with the more straight forward version, the “Clausius Postulate”
No cyclic process is possible whose sole outcome is transfer of heat from a cooler body to a hotter body
and the more modern but equivalent “Kelvin-Plank Postulate”:
No cyclic process is possible whose sole outcome is extraction of heat from a single source maintained at constant temperature and its complete conversion into mechanical work
How then can such statements be distorted into defending Intelligent Design? I argue ID does not follow from these postulates and ID proponents and creationists do not serve their cause well by making appeals to the 2nd law.
I will give illustrations first from classical thermodynamics and then from the more modern versions of statistical thermodynamics.
The notion of “entropy” was inspired by the 2nd law. In classical thermodynamics, the notion of order wasn’t even mentioned as part of the definition of entropy. I also note, some physicists dislike the usage of the term “order” to describe entropy:
Let us dispense with at least one popular myth: “Entropy is disorder” is a common enough assertion, but commonality does not make it right. Entropy is not “disorder”, although the two can be related to one another. For a good lesson on the traps and pitfalls of trying to assert what entropy is, see Insight into entropy by Daniel F. Styer, American Journal of Physics 68(12): 1090-1096 (December 2000). Styer uses liquid crystals to illustrate examples of increased entropy accompanying increased “order”, quite impossible in the entropy is disorder worldview. And also keep in mind that “order” is a subjective term, and as such it is subject to the whims of interpretation. This too mitigates against the idea that entropy and “disorder” are always the same, a fact well illustrated by Canadian physicist Doug Craigen, in his online essay “Entropy, God and Evolution”.
From classical thermodynamics, consider the heating and cooling of a brick. If you heat the brick it gains entropy, and if you let it cool it loses entropy. Thus entropy can spontaneously be reduced in local objects even if entropy in the universe is increasing.
Consider the hot brick with a heat capacity of C. The change in entropy delta-S is defined in terms of the initial hot temperature TH and the final cold temperature TM:
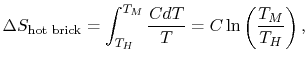
Supposing the hot temperature TH is higher than the final cold temperature TM, then Delta-s will be NEGATIVE, thus a spontaneous reduction of entropy in the hot brick results!
The following weblink shows the rather simple calculation of how a cold brick when put in contact with a hot brick, reduces spontaneously the entropy of the hot brick even though the joint entropy of the two bricks increases. See: Massachussetts Institute of Technology: Calculation of Entropy Change in Some Basic Processes
So it is true that even if universal entropy is increasing on average, local reductions of entropy spontaneously happen all the time.
Now one may argue that I have used only notions of thermal entropy, not the larger notion of entropy as defined by later advances in statistical mechanics and information theory. But even granting that, I’ve provided a counter example to claims that entropy cannot spontaneously be reduced. Any 1st semester student of thermodynamics will make the calculation I just made, and thus it ought to be obvious to him, than nature is rich with example of entropy spontaneously being reduced!
But to humor those who want a more statistical flavor to entropy rather than classical notions of entropy, I will provide examples. But first a little history. The discipline of classical thermodynamics was driven in part by the desire to understand the conversion of heat into mechanical work. Steam engines were quite the topic of interest….
Later, there was a desire to describe thermodynamics in terms of classical (Newtonian-Lagrangian-Hamiltonian) Mechanics whereby heat and entropy are merely statistical properties of large numbers of moving particles. Thus the goal was to demonstrate that thermodynamics was merely an extension of Newtonian mechanics on large sets of particles. This sort of worked when Josiah Gibbs published his landmark treatise Elementary Principles of Statistical Mechancis in 1902, but then it had to be amended in light of quantum mechanics.
The development of statistical mechanics led to the extension of entropy to include statistical properties of particles. This has possibly led to confusion over what entropy really means. Boltzmann tied the classical notions of entropy (in terms of heat and temperature) to the statistical properties of particles. This was formally stated by Plank for the first time, but the name of the equation is “Boltzmann’s entropy formula”:

where “W” (omega) is the number of microstates (a microstate is roughly the position and momentum of a particle in classical mechanics, its meaning is more nuanced in quantum mechanics). So one can see that the notion of “entropy” has evolved in physics literature over time….
To give a flavor for why this extension of entropy is important, I’ll give an illustration of colored marbles that illustrates increase in the statistical notion of entropy even when no heat is involved (as in classical thermodynamics). Consider a box with a partition in the middle. On the left side are all blue marbles, on the right side are all red marbles. Now, in a sense one can clearly see the arrangement is highly ordered since marbles of the same color are segregated. Now suppose we remove the partition and shake the box up such that the red and blue marbles mix. The process has caused the “entropy” of the system to increase, and only with some difficulty can the original ordering be restored. Notice, we can do this little exercise with no reference to temperature and heat such as done in classical thermodynamics. It was for situations like this that the notion of entropy had to be extended to go beyond notions of heat and temperature. And in such cases, the term “thermodynamics” seems a little forced even though entropy is involved. No such problem exists if we simply generalize this to the larger notion of statistical mechanics which encompasses parts of classical thermodynamics.
The marble illustration is analogous to the mixing of different kinds of distinguishable gases (like Carbon-Dioxide and Nitrogen). The notion is similar to the marble illustration, it doesn’t involve heat, but it involves increase in entropy. Though it is not necessary to go into the exact meaning of the equation, for the sake of completeness I post it here. Notice there is no heat term “Q” for this sort of entropy increase:

where R is the gas constant, n the total number of moles and xi the mole fraction of component, and Delta-Smix is the change in entropy due to mixing.
But here is an important question, can mixed gases, unlike mixed marbles spontaneously separate into localized compartments? That is, if mixed red and blue marbles won’t spontaneously order themselves back into compartments of all blue and red (and thus reduce entropy), why should we expect gases to do the same? This would seem impossible for marbles (short of a computer or intelligent agent doing the sorting), but it is a piece of cake for nature even though there are zillions of gas particles mixed together. The solution is simple. In the case of Carbon Dioxide, if the mixed gases are brought to a temperature that is below -57 Celcius (the boiling point of Carbon Dioxide) but above -195.8 Celcius (the boiling point of Nitrogen), the Carbon Dioxide will liquefy but the Nitrogen will not, and thus the two species will spontaneously separate and order spontaneously re-emerges and entropy of the local system spontaneously reduces!
Conclusion: ID proponents and creationists should not use the 2nd Law to defend their claims. If ID-friendly dabblers in basic thermodynamics will raise such objections as I’ve raised, how much more will professionals in physics, chemistry, and information theory? If ID proponents and creationists want to argue that the 2nd Law supports their claims but have no background in these topics, I would strongly recommend further study of statistical mechanics and thermodynamics before they take sides on the issue. I think more scientific education will cast doubt on evolutionism, but I don’t think more education will make one think that 2nd Law arguments are good arguments in favor of ID and the creation hypothesis.
UPDATE:
Dr. Sewell has been kind enough to respond. He pointed out my oversight of not linking to his papers. My public apologies to him. His response contains links to his papers.
Response to scordova
UPDATE:
at the request of Patrick at SkepticalZone, I am providing a link to his post which provides links to others discussions of Dr. Sewell’s work. I have not read these other critiques, and for sure, they may not have much attempt at civility. But because Skeptical Zone has been kind enough to publish my writings, I have some obligation to reciprocate. Again, I have not read those critiques. What I have written was purely in response to the Evolution News and Views postings regarding the topic of thermodynamics.