In 2005, David L Abel and Jack T Trevors published a key article on order, randomness and functionality, that sets a further context for appreciating the warrant for the design inference.
The publication data and title for the peer-reviewed article are as follows:
|
Theor Biol Med Model. 2005; 2: 29.
Published online 2005 August 11. doi: 10.1186/1742-4682-2-29.
|
PMCID: PMC1208958
|
_________________
We may discuss this figure in steps:
1 –> The data structure T & A have in view is the string, where symbols are chained in a line like:
c-h-a-i-n-e-d
2 –> Since any other data structure can be built up from a combination of strings, this is without loss of generality.
3 –> They then envision three types of sequences:
(a) orderly ones that are repetitive:
jjjjjjjjjjjjjjjjjjjj
(b) random ones that are essentially incompressible:
f3erug4huevb
(c) functional ones, that are almost as incompressible, but are constrained by that functionality:
this is a functional, non- orderly and non-random sequence
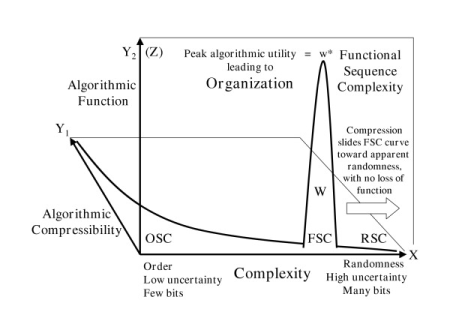
4 –> Fig 4 then shows how these three types of sequences can be represented in a 3-dimensional space that in principle can be a metric: for, order and randomness are on two ends of a continuum of compressibility and a similar continuum of complexity, both being low on algorithmic [or, by extension, linguistic-contextual] functionality.
5 –> The location of the FSC peak is particularly revealing: first, it is not quite as incompressible as a truly random sequence, because there is normally some redundancy in meaningful messages. So, the Shannon Information carrying capacity metric is not quite what is needed.
6 –> Compressibility metrics will show that FSC sequences will be slightly less resistant to compression than are truly random sequences — for the latter, to communicate them, you essentially have to quote them.
7 –> By contrast, an orderly sequence can be compressed by giving its unit cell then saying replicate n times. It is highly compressible.
8 –> But neither orderly nor random sequences are generally able to function, and so we see a sharp peak in the curve as we hit the FSC.
9 –> If we imagine the curve as sitting in a sea that floods the diagram, we can see how the image of islands of isolated function can emerge: FSC peaks up out of the sea of non-functional orderly or random sequences. And of course, functionality is always in a context: parts or components or elements combine to do the job in hand.
10 –> J S Wicken, in his key 1979 remarks, captures the next key point: we routinely and habitually observe that functional sequences are the product of design, and thus they are a longstanding puzzle for those who would account for living forms on natural selection:
‘Organized’ systems are to be carefully distinguished from ‘ordered’ systems. Neither kind of system is ‘random,’ but whereas ordered systems are generated according to simple algorithms [i.e. “simple” force laws acting on objects starting from arbitrary and common- place initial conditions] and therefore lack complexity, organized systems must be assembled element by element according to an external ‘wiring diagram’ with a high information content . . . Organization, then, is functional complexity and carries information. It is non-random by design or by selection, rather than by the a priori necessity of crystallographic ‘order.’[“The Generation of Complexity in Evolution: A Thermodynamic and Information-Theoretical Discussion,” Journal of Theoretical Biology, 77 (April 1979): p. 353, of pp. 349-65. (Emphases and note added. Also, the idea-roots of a term commonly encountered at UD, functionally specific, complex information [FSCI], should be obvious. The onward restriction to digitally coded FSCI [dFSCI] as is seen in DNA — and as will feature below, should also be obvious.)]
11 –>We can compose a simple metric that would capture the idea: Where function is f, and takes values 1 or 0 [as in pass/fail], complexity threshold is c [1 if over 1,000 bits, 0 otherwise] and number of bits used is b, we can measure FSCI in functionally specific bits, as the simple product:
FX = f*c*b, in functionally specific bits
12 –> Actually, we commonly see such a measure; e.g. when we see that a document is say 197 kbits long, that means it is functional as say an Open Office Writer document, is complex and uses 197 k bits storage space.
[Continued, here]