[Continued, from here]
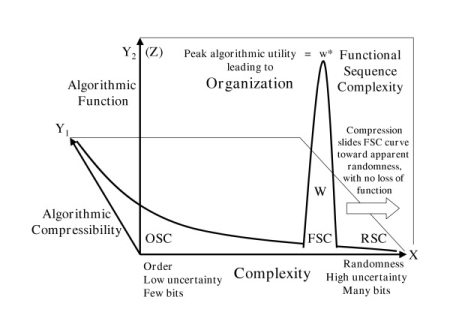
13 –> Durston et al, in 2007, extended this reasoning, by creating a more sophisticated metric that they used to measure the FSC value, in functional bits, or FITS, for 35 protein families [where a certain range of variants are functional, folding correctly and being biologically active]; which was again published as a peer-reviewed article. Excerpting the UD Weak Argument Correctives, no 27:
[an] empirical approach to measuring functional information in proteins has been suggested by Durston, Chiu, Abel and Trevors in their paper “Measuring the functional sequence complexity of proteins”, and is based on an application of Shannon’s H (that is “average” or “expected” information communicated per symbol: H(Xf(t)) = -∑P(Xf(t)) logP(Xf(t)) ) to known protein sequences in different species.
14 –> For completeness, from the paper, we see the specific FSC metric in FITS, in Eqn 6:
The measure of Functional Sequence Complexity, denoted as ζ, is defined as the change in functional uncertainty from the ground state H(Xg(ti)) to the functional state H(Xf(ti)), or
ζ = ΔH (Xg(ti), Xf(tj)).(6)
The resulting unit of measure is defined on the joint data and functionality variable, which we call Fits (or Functional bits). The unit Fit thus defined is related to the intuitive concept of functional information, including genetic instruction and, thus, provides an important distinction between functional information and Shannon information[6,32].
Eqn. (6) describes a measure to calculate the functional information of the whole molecule, that is, with respect to the functionality of the protein considered.
15 –> The somewhat broader concept, complex specified information, has also been quantified, and the same WAC27 continues:
A more general approach to the definition and quantification of CSI can be found in a 2005 paper by Dembski: “Specification: The Pattern That Signifies Intelligence”.
For instance, on pp. 17 – 24, he argues:
define ϕS as . . . the number of patterns for which [agent] S’s semiotic description of them is at least as simple as S’s semiotic description of [a pattern or target zone] T. [26] . . . . where M is the number of semiotic agents [S’s] that within a context of inquiry might also be witnessing events and N is the number of opportunities for such events to happen . . . . [where also] computer scientist Seth Lloyd has shown that 10^120 constitutes the maximal number of bit operations that the known, observable universe could have performed throughout its entire multi-billion year history.[31] . . . [Then] for any context of inquiry in which S might be endeavoring to determine whether an event that conforms to a pattern T happened by chance, M·N will be bounded above by 10^120. We thus define the specified complexity [χ] of T given [chance hypothesis] H [in bits] . . . as [the negative base-2 logarithm of the conditional probability P(T|H) multiplied by the number of similar cases ϕS(t) and also by the maximum number of binary search-events in our observed universe 10^120]
χ = – log2[10^120 ·ϕS(T)·P(T|H)].
To illustrate consider a hand of 13 cards with all spades, which is unique. 52 cards may have 635 *10^9 possible combinations, giving odds of 1 in 635 billions as P(T|H). Also, there are four similar all-of-one-suite hands, so ϕS(T) = 4. Calculation yields χ = -361, i.e. < 1, so that such a hand is not improbable enough that the – rather conservative — χ metric would conclude “design beyond reasonable doubt.” (If you see such a hand in the narrower scope of a card game, though, you would be very reasonable to suspect cheating.)
+++++++++++++
So, we see how we can contrast order, randomness and organisation for function, identifying measurements that can quantify our observations. This now completes a basic background for addressing the warrant for the design inference.