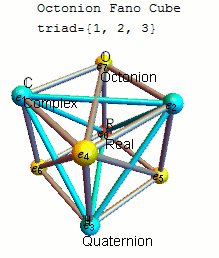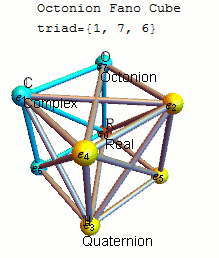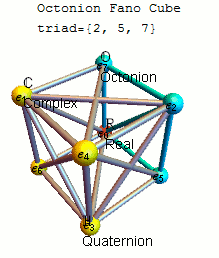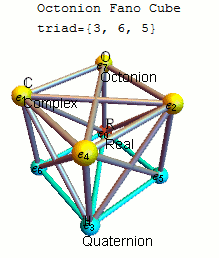
Some think that the properties of our universe are based on strange numbers which have eight dimensions, called octonions:
An Irish mathematician by the name of William Rowan Hamilton discovered in 1843 that if you pair the complex numbers in a certain way, they can form 4-D “quaternions.” He was apparently so excited about figuring out that formula, that he immediately carved it into the Broome Bridge in Dublin. Not to be outdone, John Graves, a friend of Hamilton’s who was a lawyer and math whiz, showed that quarternions can be paired up to become “octonions” – numbers that can assume coordinates in an abstract 8-dimensional (8-D) space.
…
The mystery of these numbers has led to speculation among researchers that they have a special purpose and can eventually explain the deeper secrets of the universe. In an email interview with Quanta Magazine, the particle physicist Pierre Ramond from the University of Florida explained that “Octonions are to physics what the Sirens were to Ulysses.” Paul Ratner, “Physicists puzzled by strange numbers that could explain reality” at BigThink
Well, if all that New Year’s partying out there is keeping you awake, here is more on octonions.
See also these odd number facts: New Scientist on the glitch at the edge of the universe (the saga of the strange number 137)
and
Prime numbers are not nearly as scattershot as previously thought
Follow UD News at Twitter!