As known, complex numbers are numbers of the form:
z = x + i y
where x is the real part, y is the imaginary part and “i” is the square root of -1. Complex numbers have many applications in science, where it is necessary, in the same time, to collect together and discriminate two heterogeneous entities. Here, as brainstorming, I propose to consider complex numbers when we deal with the complexity/organization of systems. We could define the measure of the “complexity c(S) of a system S” as a complex number z:
c(S) = z = x + i y = quantity + i quality = matter + i information
where x is a measure of its quantitative aspects (mass, weight, number of molecules…) and y is a measure of its qualitative aspects (shapes, complexity, organization, information, functional CSI…). See also my previous post about Quality quantity and intelligent design.
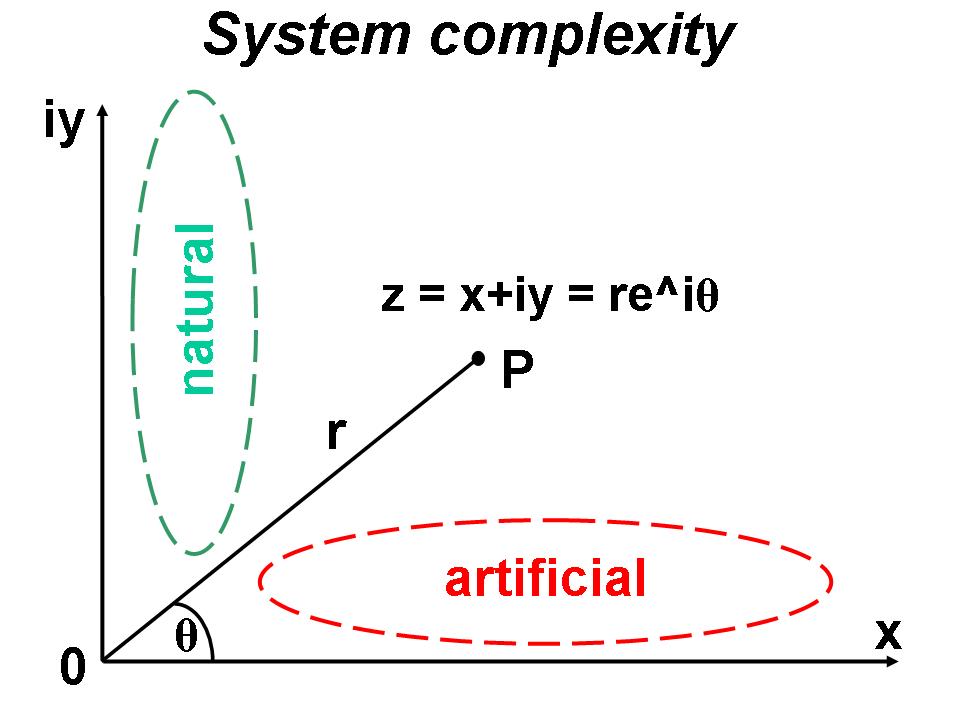
Complex numbers can be represented as points on a special Cartesian plane called “complex plane”. Roughly speaking, if we represent all systems existent on Earth on this complex plane, we get something like this:
The green “cloud” groups the natural systems. They typically have low x and high y (ex. bacteria, cells, organisms…). The red “cloud” groups the artificial systems. They typically have high x and low y (ex. machines, airplanes, ships, buildings…). Of course these “low y” values of the artificial systems are low only in comparison to the natural systems, because just the artificial systems contains large amount of organization. The natural systems are more complex because their Designer is incomparably more intelligent than the human designers.
—
Now, let’s consider a system as composed of sub-systems. For clarity, take a mousetrap M that has five parts/sub-systems. Their individual complexity will be:
z1 = x1 + iy1
z2 = x2 + iy2
z3 = x3 + iy3
z4 = x4 + iy4
z5 = x5 + iy5
The overall complexity of their set union c(U(zn)) will be the sum of the complexities of the individual parts:
c(U(zn)) = z1+z2+z3+z4+z5=
(x1+x2+x3+x4+x5) + i(y1+y2+y3+y4+y5)
Warning: this set union is not at all the assembled mousetrap M, rather the simple collection of its parts disconnected and dispersed on the table. Instead the complexity c(M) of the assembled mousetrap M will be:
c(M) = (x1+x2+x3+x4+x5) + i(y1+y2+y3+y4+y5+a) = c(U(zn)) + ia
In words, the complexity c(M) of the assembled mousetrap is the complexity of their set union c(U(zn)) + an imaginary factor “ia” where “a” stands for “assembly”. In fact, the quantitative aspects (represented by the real part x) will be identical (the mass/weight of the mousetrap is equal to the mass/weight of its sparse parts). The difference must be represented by an additional factor related to the assembly. This additional factor is necessarily an add-on to the imaginary part y. It is thanks to the “a” factor that the mousetrap can work, while its parts, when disassembled, don’t work.
The above use of complex numbers leads us to two observations:
(1) We are helped to understand that intelligent design is something eminently qualitative, which can arise also when the quantity involved in the system is exactly the same.
(2) An evolutionary material process that simply adds molecules, may increase the quantitative real part x of the complexity z of a system S. But, by definition, it is incapable to increase the qualitative imaginary part y of its complexity.
—
By using Euler’s formula we have the polar form of a complex number:
z = r(cosθ + i sinθ) = re^iθ
where “r” is the modulus of z (the length of the segment OP) and θ is the angle of the segment OP related to the x axis (see the figure above).
A “system” containing pure quantity, i.e. quality/design equal zero, has θ = 0, then
c(quantity) = z = re^i0 = r
Differently, pure quality/design, i.e. quantity equal zero, has θ = π/2 (Greek pi / 2), then
c(quality/design) = z = re^iπ/2
Note that quality/design appears when the more significant numbers of mathematics — 1, 2, e, π, i — appear. This emphasizes the strong relation between mathematics and intelligent design. Since the entire cosmos is a “grand design”, its Designer is also the Great Mathematician, who said “I created the Heaven and the Earth only by means of the Truth”.