Granville Sewell and Daniel Styer have a thing in common: both wrote an article with the same title “Entropy and evolution”. But they reach opposite conclusions on a fundamental question: Styer says that the evolutionist “compensation argument” (henceforth “ECA”) is ok, Sewell says it isn’t. Here I briefly explain why I fully agree with Granville. The ECA is an argument that tries to resolve the problems the 2nd law of statistical mechanics (henceforth 2nd_law_SM) posits to unguided evolution. I adopt Styer’s article as ECA archetype because he also offers calculations, which make clearer its failure.
The 2nd_law_SM as problem for evolution.
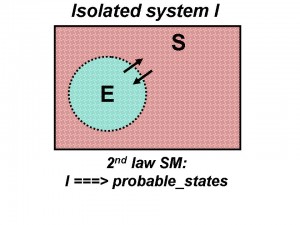
The 2nd_law_SM says that a isolated system goes toward its more probable macrostates. In this diagram the arrow represents the 2nd_law_SM rightward trend/direction:
organization … improbable_states … systems ====>>> probable_states
Sewell says:
“The second law is all about using probability at the microscopic level to predict macroscopic change. […] This statement of the second law, or at least of the fundamental principle behind the second law, is the one that should be applied to evolution.”
The physical evolution of a isolated system passes spontaneously through macrostates with increasing values of probability until arriving to equilibrium (the most probable macrostate). Since organization is highly improbable a corollary of the 2nd_law_SM is that isolated systems don’t self-organize. That is the opposite of what biological evolution pretends.
See the picture:
Styer’s ECA.
Since the 2nd_law_SM applies to isolated systems the ECA says: the Earth E is not a isolated system, then its entropy can decrease thanks to an entropy increase (compensation) in the surroundings S (wrt to the energy coming from the Sun). Unfortunately to consider open the systems is useless, because, as Sewell puts it:
“If an increase in order is extremely improbable when a system is closed, it is still extremely improbable when the system is open, unless something is entering which makes it not extremely improbable.”
Here is how Styer applies the ECA to show that “evolution is consistent with the 2nd law”.
Suppose that, due to evolution, each individual organism is 1000 times more improbable that the corresponding individual was 100 years ago (Emory Bunn says 1000 times is incorrect, it should be 10^25 times, but this is a detail). If Wi is the number of microstates consistent with the specification of an initial organism I 100 years ago, and Wf is the number of microstates consistent with the specification of today’s improved and less probable organism F, then
Wf = Wi / 1000
At this point he uses Boltzmann’s formula:
S = k * ln (W)
where S = entropy, W = number of microstates, k = 1.38 x 10^-23 joules/degrees, ln = logarithm.
Then he calculates the entropy change over 100 years, and finally the entropy decrease per second:
Sf – Si = -3.02 x 10^-30 joules/degrees
By considering all individuals of all species he gets the change in entropy of the biosphere each second: -302 joules/degrees. Since he knows that the Earth’s physical entropy throughput (due to energy from the Sun) each second is: 420 x 10^12 joules/degrees he concludes: “at a minimum the Earth is bathed in about one trillion times the amount of entropy flux required to support the rate of evolution assumed here”, then evolution is largely consistent with the 2nd law.
The problem in Styer’s argument (and in general in the ECA).
Although it could seem an innocent issue of measure units the introduction of the Boltzmann’s formula with k = 1.38 x 10^-23 joules/degrees in this context is a conceptual error. With such formula the ECA has transformed a difficult problem of probability (in connection with the arise of ultra-complex organized systems) into a simple issue of energy (“joule” is unit of energy, work, or amount of heat). This assumes a priori that energy is able to organize organisms from sparse atoms. But such assumption is totally gratuitous and unproved. That energy can do that is exactly what the ECA should prove in the first place. So Styer’s ECA begs the question.
Similarly Andy McIntosh (cited by Sewell) says:
Both Styer and Bunn calculate by slightly different routes a statistical upper bound on the total entropy reduction necessary to ‘achieve’ life on earth. This is then compared to the total entropy received by the Earth for a given period of time. However, all these authors are making the same assumption—viz. that all one needs is sufficient energy flow into a [non-isolated] system and this will be the means of increasing the probability of life developing in complexity and new machinery evolving. But as stated earlier this begs the question…
The Boltzmann’s formula in the ECA, with its introduction of joules of energy, establishes a bridge between probabilities and the joules coming from the Sun. Unfortunately this link is unsubstantiated here because no one has proved that joules cause biological organization. On the contrary, in my previous post “The illusion of organizing energy” I explained why any kind of energy per se cannot create organization in principle. To greater reason, thermal energy is unable to the task. In fact, heat is the more degraded and disordered kind of energy, the one with maximum entropy. So the ECA would contain also an internal contradiction: by importing entropy in E one decreases entropy in E!
The problem of Boltzmann’s formula, as used in the ECA, is then “to buy” probability bonus with energy “money”. Sewell expresses the same concept with different words:
The compensation argument is predicated on the idea […] that the universal currency for entropy is thermal entropy.
That conversion / compensation is not allowed if one hasn’t proved at the outset a direct causation role of energy in producing the effect, biological organization, which is in the opposite direction of the 2nd_law_SM rightward arrow (extreme left on the above diagram). In a sense the ECA conflates two different planes. This wrong conflation is like to say that a roulette placed inside a refrigerated room can easily output 1 million “black” in a row because its entropy is decreased compared to the outside.
Note that evolution doesn’t imply a single small deviation from the trend, quite differently it implies countless highly improbable processes happened continually in countless organisms during billion years. Who claims that evolution doesn’t violate the 2nd_law_SM, would doubt a violation if countless tornados always turned rubble into houses, cars and computers for billion years? Sewell asks (backward tornado is the metaphor he uses more). In conclusion Roger Caillois is right: “Clausius and Darwin cannot both be right.”
Implausibility of evolution.
Styer’s paper is also an opportunity to see the problem of evolution from a probabilistic viewpoint. You will note the huge difference of difficulty of the probabilistic scenario compared to the above enthusiastic thermal entropy scenario, with potentially 1,000,000,000,000 times evolution!
In Appendix #2 he proposes a problem for students: “How much improved and less probable would each organism be, relative to its (possibly single-celled) ancestor at the beginning of the Cambrian explosion? (Answer: 10 raised to the 1.8 x 10^22 times)”. Call this monster number “a”, Wi = the initial microstates, Wf = the final microstates, W = the total microstates. According to Styer’s answer (which is correct as calculation) we have:
Wf = Wi / a
The probability of the initial macrostate is Wi / W. The probability of the final macrostate is Wf / W. Suppose Wf = 1, then Wi is = a. W must be equal or greater a otherwise (Wi / W) would be greater than 1 (impossible). Therefore the probability to occur of the final macrostate is:
(Wf / W) equal or less (1 / a)
This is the probability of evolution of a single individual organism in the Cambrian:
1 on 10 raised to the 1.8 x 10^22
a number with more than 10^22 digits (10 trillion billion digits). This miraculous event had to occur 10^18 times, for each of other organisms.
Dembski’s “universal probability bound” is:
1 / 10^150
1 on a number with “only” 150 digits. Therefore evolution is far beyond the plausibility threshold. In conclusion: the ECA fails to prove that “evolution is consistent with the 2nd law”, and we have also a proof of the implausibility of evolution based on probability.
Some could object: “you cannot have both ways, if the ECA is wrong then Appendix #2 is wrong too, because it uses the same method, then the evolution probability is not correct”.
Answer: the method is biased toward evolution both in ECA and in Appendix #2. This means the evolution probability is even worse than that, and the implausibility of evolution holds to greater reason.