If even scientists can’t easily explain p-values… ?

_{Denyse O'Leary

December 2, 2015

Intelligent Design, News, Science}

Share: Facebook; Twitter; LinkedIn; Flipboard; Print; Email

Further to astronomer Hugh Ross on degrees of certainty in science, from Christie Aschwanden, Five Thirty-Eight’s lead science writer:

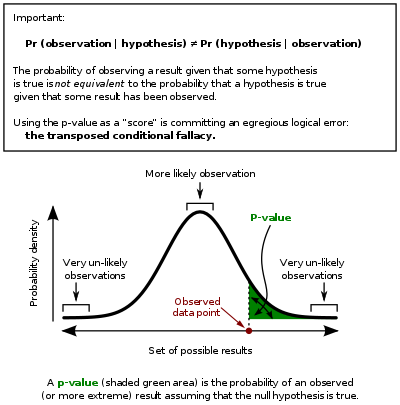
P-values have taken quite a beating lately. These widely used and commonly misapplied statistics have been blamed for giving a veneer of legitimacy to dodgy study results, encouraging bad research practices and promoting false-positive study results.

But after writing about p-values again and again, and recently issuing a correction on a nearly year-old story over some erroneous information regarding a study’s p-value (which I’d taken from the scientists themselves and their report), I’ve come to think that the most fundamental problem with p-values is that no one can really say what they are. More.

Here’s the theory, from Dummies, but apparently no one finds it easy to understand in practice:

For example, suppose a pizza place claims their delivery times are 30 minutes or less on average but you think it’s more than that. You conduct a hypothesis test because you believe the null hypothesis, Ho, that the mean delivery time is 30 minutes max, is incorrect. Your alternative hypothesis (Ha) is that the mean time is greater than 30 minutes. You randomly sample some delivery times and run the data through the hypothesis test, and your p-value turns out to be 0.001, which is much less than 0.05. In real terms, there is a probability of 0.001 that you will mistakenly reject the pizza place’s claim that their delivery time is less than or equal to 30 minutes. Since typically we are willing to reject the null hypothesis when this probability is less than 0.05, you conclude that the pizza place is wrong; their delivery times are in fact more than 30 minutes on average, and you want to know what they’re gonna do about it! (Of course, you could be wrong by having sampled an unusually high number of late pizza deliveries just by chance.)

See also: Nature: Banning p-values not enough to rid science of shoddy statistics

and

Rob Sheldon explains p-value vs. R2 value in research, and why it matters

Oh, and Steven Weinberg defends “Whiggish” history of science Actually, science has nothing over these other endeavours when the question can be decided by evidence.

Follow UD News at Twitter!

Comments

If p-value is a probability term, -log2(p-value) is the information in bit. I wonder if “p-value” can be used to estimate CSI?
Indeed -- the last form of CSI that dembski defended was a reformulation of statistical hypothesis testing.wd400_{December 4, 2015
December
12
Dec
4
04
2015
09:43 AM
9
09
43
AM
PDT}

I think p-value is a very clear and useful concept. It is true that many who use it don't understand what it is (that is sadly true in medicine!). And yes, when we evaluate dFSCI (or CSI) we use a form of probability under null hypothesis: more or less, for example, for a functional protein, we ask: what is the probability to get to a protein which exhibits at least a pre-defined level of a pre-defined function if we assume that the observed functional protein came into existence by a random walk from some unrelated sequence? And then we compare that probability with the probabilistic resources available in a natural system.gpuccio_{December 4, 2015
December
12
Dec
4
04
2015
08:44 AM
8
08
44
AM
PDT}

If p-value is a probability term, -log2(p-value) is the information in bit. I wonder if "p-value" can be used to estimate CSI? The consequence is that many statistical tests can then be used to estimate the p term in CSI. From wiki, "the p-value is defined as the probability of obtaining a result equal to or "more extreme" than what was actually observed, assuming that the hypothesis under consideration is true."bonebone_{December 4, 2015
December
12
Dec
4
04
2015
08:31 AM
8
08
31
AM
PDT}

That "For dummies" example is pretty awful. The real definition is not hard to grasp: it's the probability of getting a data equal to or more extreme than an observed value if a null hypothesis is true. The problems only arise when we people miss-specify a null hypothesis or conflate this probability with an event happening "by chance", the probability the null hypothesis is true or the probability some alternative hypothesis is false. (Or whatever Rob Sheldon is going on about in that linked post).wd400_{December 3, 2015
December
12
Dec
3
03
2015
01:10 PM
1
01
10
PM
PDT}

great intuitive view of probability and random chance tookairosfocus_{December 3, 2015
December
12
Dec
3
03
2015
08:03 AM
8
08
03
AM
PDT}

You need to have a fair understanding of what sort of distribution and mean would make sense for a null, or a p-value connected to say a normal curve can be very misleading. Do you have an idea of a very large cluster of small effectively unbiased errors pushing a particular observation this way and that at random around a mean? Try a Galton Board, cf vid: https://www.youtube.com/watch?v=9tTHST1sLV8 here is a professional version: https://www.youtube.com/watch?v=AUSKTk9ENzg If that is not plausible, normal curve circumstances do not obtain, though this is hardly the only possibility. KFkairosfocus_{December 3, 2015
December
12
Dec
3
03
2015
07:48 AM
7
07
48
AM
PDT}

Although mathematics and real time testing certainly play a very important part, 'observation' is the backbone of science. This is where Darwinian evolution and Intelligent Design drastically part company. Whereas we know for 100% certainty that intelligence can generate non-trivial functional information, no one has ever observed even one instance of unguided material processes generating non-trivial functional information. In fact, just one 'observed' instance would falsify ID.
The Law of Physicodynamic Incompleteness - David L. Abel Excerpt: "If decision-node programming selections are made randomly or by law rather than with purposeful intent, no non-trivial (sophisticated) function will spontaneously arise." If only one exception to this null hypothesis were published, the hypothesis would be falsified. Falsification would require an experiment devoid of behind-the-scenes steering. Any artificial selection hidden in the experimental design would disqualify the experimental falsification. After ten years of continual republication of the null hypothesis with appeals for falsification, no falsification has been provided. The time has come to extend this null hypothesis into a formal scientific prediction: "No non trivial algorithmic/computational utility will ever arise from chance and/or necessity alone." https://www.academia.edu/Documents/in/The_Law_of_Physicodynamic_Incompleteness
In fact, Perry Marshall has organized a 3 million dollar prize for the first person who can prove that unguided material processes can generate non-trivial information:
The Origin of Information: How to Solve It - Perry Marshall Where did the information in DNA come from? This is one of the most important and valuable questions in the history of science. Cosmic Fingerprints has issued a challenge to the scientific community: “Show an example of Information that doesn’t come from a mind. All you need is one.” “Information” is defined as digital communication between an encoder and a decoder, using agreed upon symbols. To date, no one has shown an example of a naturally occurring encoding / decoding system, i.e. one that has demonstrably come into existence without a designer. A private equity investment group is offering a technology prize for this discovery. We will financially reward and publicize the first person who can solve this;,,, To solve this problem is far more than an object of abstract religious or philosophical discussion. It would demonstrate a mechanism for producing coding systems, thus opening up new channels of scientific discovery. Such a find would have sweeping implications for Artificial Intelligence research. http://cosmicfingerprints.com/solve/
There are solid mathematical reasons for believing that that 3 million dollar prize will never be collected:
Evolutionary Computing: The Invisible Hand of Intelligence - June 17, 2015 Excerpt: William Dembski and Robert Marks have shown that no evolutionary algorithm is superior to blind search -- unless information is added from an intelligent cause, which means it is not, in the Darwinian sense, an evolutionary algorithm after all. This mathematically proven law, based on the accepted No Free Lunch Theorems, seems to be lost on the champions of evolutionary computing. Researchers keep confusing an evolutionary algorithm (a form of artificial selection) with "natural evolution." ,,, Marks and Dembski account for the invisible hand required in evolutionary computing. The Lab's website states, "The principal theme of the lab's research is teasing apart the respective roles of internally generated and externally applied information in the performance of evolutionary systems." So yes, systems can evolve, but when they appear to solve a problem (such as generating complex specified information or reaching a sufficiently narrow predefined target), intelligence can be shown to be active. Any internally generated information is conserved or degraded by the law of Conservation of Information.,,, What Marks and Dembski prove is as scientifically valid and relevant as Gödel's Incompleteness Theorem in mathematics. You can't prove a system of mathematics from within the system, and you can't derive an information-rich pattern from within the pattern.,,, http://www.evolutionnews.org/2015/06/evolutionary_co_1096931.html
The reason I bring this complete lack of observational evidence for Darwinism up, is because some Darwinists a few years back tried some shenanigans with these statistical p-values to make it appear as if Darwinian evolution were something more than the atheistic pipe dream that it is.
Douglas Theobald Tests Universal Common Ancestry by Refuting a Preposterous Null Hypothesis - Casey Luskin November 29, 2010 Excerpt: National Geographic notes in a subheadline: "Creationism called 'absolutely horrible hypothesis' -- statistically speaking." The problem is that Theobald didn't test universal common ancestry against "creationism." He tested universal common ancestry against the impossibly unlikely hypothesis that these genes independently arrived at highly similar sequences via blind, unguided convergent evolution. Given his outlandish null hypothesis, no wonder common descent came out looking so good. Again, if you don't believe me, consider what reviewers of a critique of Theobald's paper had to say (link on site): Cogniscenti cringed when they saw the Theobald paper, knowing that "it is trivial". It is trivial because the straw man that Theobald attacks in a text largely formulated in convoluted legalese, is that significant sequence similarity might arise by chance as opposed to descent with modification. http://www.evolutionnews.org/2010/11/douglas_theobald_tests_univers041021.html
A few more notes on Darwinism's complete lack of 'observational' evidence:
“In science’s pecking order, evolutionary biology lurks somewhere near the bottom, far closer to phrenology than to physics. For evolutionary biology is a historical science, laden with history’s inevitable imponderables. We evolutionary biologists cannot generate a Cretaceous Park to observe exactly what killed the dinosaurs; and, unlike “harder” scientists, we usually cannot resolve issues with a simple experiment, such as adding tube A to tube B and noting the color of the mixture.” - Jerry A. Coyne – Of Vice and Men, The New Republic April 3, 2000 p.27 - professor of Darwinian evolution at the University of Chicago "Evolutionary biology, in contrast with physics and chemistry, is a historical science — the evolutionist attempts to explain events and processes that have already taken place. Laws and experiments are inappropriate techniques for the explication of such events and processes. Instead one constructs a historical narrative, consisting of a tentative reconstruction of the particular scenario that led to the events one is trying to explain." Ernst Mayr - Darwin's Influence on Modern Thought - Nov. 2009 - Originally published July 2000 “Truth be told, evolution hasn’t yielded many practical or commercial benefits. Yes, bacteria evolve drug resistance, and yes, we must take countermeasures, but beyond that there is not much to say. Evolution cannot help us predict what new vaccines to manufacture because microbes evolve unpredictably. But hasn’t evolution helped guide animal and plant breeding? Not very much. Most improvement in crop plants and animals occurred long before we knew anything about evolution, and came about by people following the genetic principle of ‘like begets like’. Even now, as its practitioners admit, the field of quantitative genetics has been of little value in helping improve varieties. Future advances will almost certainly come from transgenics, which is not based on evolution at all.” (Jerry Coyne, “Selling Darwin: Does it matter whether evolution has any commercial applications?,” reviewing The Evolving World: Evolution in Everyday Life by David P. Mindell, in Nature, 442:983-984 (August 31, 2006).) "In fact, over the last 100 years, almost all of biology has proceeded independent of evolution, except evolutionary biology itself. Molecular biology, biochemistry, and physiology, have not taken evolution into account at all." Marc Kirschner, Boston Globe, Oct. 23, 2005 "While the great majority of biologists would probably agree with Theodosius Dobzhansky’s dictum that “Nothing in biology makes sense except in the light of evolution”, most can conduct their work quite happily without particular reference to evolutionary ideas. Evolution would appear to be the indispensable unifying idea and, at the same time, a highly superflous one.” A.S. Wilkins, editor of the journal BioEssays, Introduction to "Evolutionary Processes" - (2000). "Biologists must constantly keep in mind that what they see was not designed, but rather evolved. It might be thought, therefore, that evolutionary arguments would play a large part in guiding biological research, but this is far from the case. It is difficult enough to study what is happening now. To figure out exactly what happened in evolution is even more difficult. Thus evolutionary achievements can be used as hints to suggest possible lines of research, but it is highly dangerous to trust them too much. It is all too easy to make mistaken inferences unless the process involved is already very well understood." Francis Crick - What Mad Pursuit (1988) Anti-Science Irony Excerpt: In response to a letter from Asa Gray, professor of biology at Harvard University, Darwin declared: “I am quite conscious that my speculations run quite beyond the bounds of true science.” When questioned further by Gray, Darwin confirmed Gray’s suspicions: “What you hint at generally is very, very true: that my work is grievously hypothetical, and large parts are by no means worthy of being called induction.” Darwin had turned against the use of scientific principles in developing his theory of evolution. http://www.darwinthenandnow.com/2011/10/anti-science-irony/ An Early Critique of Darwin Warned of a Lower Grade of Degradation - Cornelius Hunter - Dec. 22, 2012 Excerpt: "Many of your wide conclusions are based upon assumptions which can neither be proved nor disproved. Why then express them in the language & arrangements of philosophical induction?" (Sedgwick to Darwin - 1859),,, And anticipating the fixity-of-species strawman, Sedgwick explained to the Sage of Kent (Darwin) that he had conflated the observable fact of change of time (development) with the explanation of how it came about. Everyone agreed on development, but the key question of its causes and mechanisms remained. Darwin had used the former as a sort of proof of a particular explanation for the latter. “We all admit development as a fact of history;” explained Sedgwick, “but how came it about?”,,, For Darwin, warned Sedgwick, had made claims well beyond the limits of science. Darwin issued truths that were not likely ever to be found anywhere “but in the fertile womb of man’s imagination.” The fertile womb of man’s imagination. What a cogent summary of evolutionary theory. Sedgwick made more correct predictions in his short letter than all the volumes of evolutionary literature to come. http://darwins-god.blogspot.com/2012/12/an-early-critique-of-darwin-warned-of.html SKEPTICS OF DARWINIAN THEORY Sedgwick to Darwin "...I have read your book with more pain than pleasure. Parts of it I admired greatly, parts I laughed at till my sides were almost sore; other parts I read with absolute sorrow, because I think them utterly false and grievously mischievous." Adam Sedgwick (1785-1873) - one of the founders of modern geology. - The Spectator, 1860 http://veritas-ucsb.org/library/origins/quotes/critics.html
bornagain_{December 2, 2015
December
12
Dec
2
02
2015
04:54 PM
4
04
54
PM
PDT}

You must be logged in to post a comment.

Leave a Reply