Is Standard Calculus Notation Wrong?

_{Jonathan Bartlett

April 8, 2019

Intelligent Design, Mathematics}

Share: Facebook; Twitter; LinkedIn; Flipboard; Print; Email

We usually think of basic mathematics such as introductory calculus to be fairly solid. However, recent research by UD authors shows that calculus notation needs a revision.

Many people complain about ID by saying, essentially, “ID can’t be true because all of biology depends on evolution.” This is obviously a gross overstatement (biology as a field was just fine even before Darwin), but I understand the sentiment. Evolution is a basic part of biology (taught in intro biology), and therefore it would be surprising to biologists to find that fundamental pieces of it were wrong.

However, the fact is that oftentimes fundamental aspects of various fields are wrong. Surprisingly, this sometimes has little impact on the field itself. If premise A is faulty and leads to faulty conclusions, oftentimes workaround B can be invoked to get around A’s problems. Thus, A can work as long as B is there to get around its problems.

Anyway, I wanted to share my own experience of this with calculus. Some of you know that I published a Calculus book last year. My goal in this was mostly to counter-act the dry, boring, and difficult-to-understand textbooks that dominate the field. However, when it came to the second derivative, I realized that not only is the notation unintuitive, there is literally no explanation for it in any textbook I could find.

For those who don’t know, the notation for the first derivative is 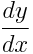. The first derivative is the ratio of the change in y (dy) compared to the change in x (dx). The notation for the second derivative is 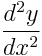. However, there is not a cogent explanation for this notation. I looked through 20 (no kidding!) textbooks to find an explanation for why the notation was the way that it was.

Additionally, I found out that the notation itself is problematic. Although it is written as a fraction, the numerator and denominator cannot be separated without causing math errors. This problem is somewhat more widely known, and has a workaround for it, known as Faa di Bruno’s formula.

My goal was to present a reason for the notation to my readers/students, so that they could more intuitively grasp the purpose of the notation. So, I decided that since no one else was providing an explanation, I would try to derive the notation myself.

Well, when I tried to derive it directly, it turns out that the notation is simply wrong (footnote – many mathematicians don’t like me using the terminology of “wrong”, but, I would argue that a fraction that can’t be treated like a fraction *is* wrong, especially when there is an alternative that does work like a fraction). Most people forget that 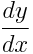is, in fact, a quotient. Therefore, the proper rule to apply to this is the quotient rule (a first-year calculus rule). When you do this to the actual first derivative notation, the notation for the second derivative (the derivative of the derivative) is actually 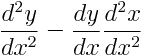. This notation can be fully treated as a fraction, and requires no secondary formulas to work with.

What does this have to do with Intelligent Design? Not much directly. However, it does show that, in any discipline, there is the possibility that asking good questions about basic fundamentals may lead to the revising of some of even the most basic aspects of the field. This is precisely what philosophy does, and I recommend the broader application of philosophy to science. Second, it shows that even newbies can make a contribution. In fact, I found this out precisely because I *was* a newbie. Finally, in a more esoteric fashion (but more directly applicable to ID), the forcing of everything into materialistic boxes limits the progress of all fields. The reason why this was not noticed before, I believe, is because, since the 1800s, mathematicians have not wanted to believe that infinitesimals are valid entities. Therefore, they were not concerned when the second derivative did not operate as a fraction – it didn’t need to, because it indeed wasn’t a fraction. Infinities and infinitesimals are the non-materialistic aspects of mathematics, just as teleology, purpose, and desire are the non-materialistic aspects of biology.

Anyway, for those who want to read the paper, it is available here:

Bartlett, Jonathan and Asatur Khurshudyan. 2019. Extending the Algebraic Manipulability of Differentials. Dynamics of Continuous, Discrete and Impulsive Systems, Series A: Mathematical Analysis 26(3):217-230.

I would love any comments, questions, or feedback.

Comments

re 69: that is exactly how I introduced calculus from day 1. You car has a clock, a speedometer, and an odometer. The clock never breaks. If the speedometer breaks, then finding the speed based on the clock and odometer leads to differentiation. If the odometer breaks, finding the distance based on the clock and the speedometer leads to integration.hazel_{April 11, 2019
April
04
Apr
11
11
2019
10:53 AM
10
10
53
AM
PDT}

Hazel@33: I agree that "infinitesimal constant" is probably an oxymoron. I don't know exactly what dx is (I always thought it was a limit), but I am fairly sure that it not a function of x. As I understand it, the quotient rule is used to find the derivative with respect to x of the ratio of two functions which are both functions of x. Here, the value of y depends on the value of x; dy depends on the value of x and one small non-zero quantity dx; but as I understand it, dx does not depend on x. Hazel@34: The comment you refer to on page 222 seems a bit strange to me. We are looking for a second derivative with respect to x, and as I understand it, we start by finding a first dirivative (dy/dx) with the respect to x and then differentiate that again - also with respect to x; If the second step involves differentiating a ratio of two functions of x, then we work out that using those functions and their derivatives with respect to x. Anyway this is all a bit beyond my pay grade, so I'll refrain from further participation (helped by the fact that I will now return home to a broken PC)- but thanks for your comments.steve_h_{April 11, 2019
April
04
Apr
11
11
2019
10:32 AM
10
10
32
AM
PDT}

PPS: I clip from his introductory case:
The derivative and integral can be described in everyday language in terms of an automobile trip. An automobile instrument panel has a speedometer marked off in miles per hour with a needle indicating the speed. The instrument panel also has an odometer which tallies up the distance travelled in miles (the mileage). Both the speedometer reading and the odometer reading change with time; that is, they are both “functions of time.” The speed shown on the speedometer is the rate of change, or derivative, of the distance. Speed is found by taking a very small interval of time and forming the ratio of the change in distance to the change in time. The distance shown on the odometer is the integral of the speed from time zero to the present. Distance is found by adding up the distance travelled from the first use of the car to the present.
Here, we see a familiar case and the concept that the Calculus is the quantitative study of rates and accumulations of change. It also opens the way to seeing how the two key operations are coupled, mutual inverses, hence for example the approach that the Integral is in practical terms often studied as the anti-derivative.kairosfocus_{April 11, 2019
April
04
Apr
11
11
2019
10:25 AM
10
10
25
AM
PDT}

kf writes, "I believe in concrete then pictorial then abstract. I also favour a learning spiral approach by which activities “loop through” key themes in building learning, interconnecting and augmenting as topics are built up cumulatively to fulfill adequate understanding and function." Very good - I agree with both the points kf mentions.hazel_{April 11, 2019
April
04
Apr
11
11
2019
09:50 AM
9
09
50
AM
PDT}

H, I am thinking more, high school. I recently saw a UK 4-5th form GCSE Math text and they are now bringing in Calculus beginnings. That's 15 - 16+ year olds. For College, I think more formal stuff is on the cards, though I strongly tend to use instructive initial case studies; a structured appreciation of quantity domains seems a part, and hyperreals have a place. As a moderate, Richard Skemp constructivist, I believe in concrete then pictorial then abstract. I also favour a learning spiral approach by which activities "loop through" key themes in building learning, interconnecting and augmenting as topics are built up cumulatively to fulfill adequate understanding and function. KF PS: Keisler's text may be a useful reference: http://www.math.wisc.edu/~keisler/keislercalc-12-23-18.pdfkairosfocus_{April 11, 2019
April
04
Apr
11
11
2019
09:04 AM
9
09
04
AM
PDT}

Dang, y'all. I step out for a day, thinking that the conversation is winding down, and it doubles. I'll try to look through this this weekend.johnnyb_{April 11, 2019
April
04
Apr
11
11
2019
06:52 AM
6
06
52
AM
PDT}

re 54: Yes. The hyperreals may have some purpose someplace, but at the level of calculus we have been discussing here - high school and standard college classes, the idea of limit as h -> 0 is standard. While teaching I would use the phrase informal phrase "becomes infinitely small" to refer to the idea of some process approaching a limit, but I think my students understood well what we meant.hazel_{April 11, 2019
April
04
Apr
11
11
2019
05:13 AM
5
05
13
AM
PDT}

KF,
DS, I spoke in those descriptive terms to point to trends and reflecting how the whole process was highly informal and in key parts inductive on key case studies.
At some point we need to be precise, however. When you speak of examining the value of (f(x + h) - f(x))/h for h "trending infinitesimal", it appears you are considering real numbers h which are really, really small, but not infinitesimal. That is, informally calculating a limit in the usual way. You do not need the hyperreal numbers to accomplish this, so is there a point in bringing them up? Is there any reason to use the word "infinitesimal" when they actually do not exist in the real numbers? My suggestion: you can speak of the limit of the difference quotient as h tends to 0 in the real numbers.daveS_{April 11, 2019
April
04
Apr
11
11
2019
04:58 AM
4
04
58
AM
PDT}

PS: Oopsie, 10^400 in 48. 200 ord mag smaller.kairosfocus_{April 11, 2019
April
04
Apr
11
11
2019
03:31 AM
3
03
31
AM
PDT}

F/N: I should also note that as the chord tends to the tangent, the deviation from a straight line becomes smaller and smaller, suggesting again that one may set aside higher order terms in the equivalent power series. Where, in the thinking of the Calculus foundation era, such series representation was never far from the surface, as curve fitting per difference terms will show and as the Newton-Raphson method shows. KFkairosfocus_{April 11, 2019
April
04
Apr
11
11
2019
02:50 AM
2
02
50
AM
PDT}

DS, I spoke in those descriptive terms to point to trends and reflecting how the whole process was highly informal and in key parts inductive on key case studies. IIRC, Leibniz used an instructive example to develop integration, which in its classical forms, again was largely intuitive. Formalisation came along 50 years ago, and may yet re-open some of the power of the approach of acknowledged giants. KFkairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
11:22 PM
11
11
22
PM
PDT}

One advantage of the hyperreals is that we don't have to use the prefix "quasi" so much.daveS_{April 10, 2019
April
04
Apr
10
10
2019
08:45 PM
8
08
45
PM
PDT}

F/N: I observe, further on in the Wikipedia article:
The use of the standard part in the definition of the derivative is a rigorous alternative to the traditional practice of neglecting the square[citation needed] of an infinitesimal quantity. Dual numbers are a number system based on this idea. After the third line of the differentiation above, the typical method from Newton through the 19th century would have been simply to discard the dx^2 term. In the hyperreal system, dx^2 not_equal 0, since dx is nonzero, and the transfer principle can be applied to the statement that the square of any nonzero number is nonzero. However, the quantity dx^2 is infinitesimally small compared to dx; that is, the hyperreal system contains a hierarchy of infinitesimal quantities.
This should help us to see the line of descent in the history of ideas, and why the older practice was workable. Standard part reduction in effect works around the problems of how does one get to higher order terms vanishing. KFkairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
08:22 PM
8
08
22
PM
PDT}

DS, I simply used a description and reported a practice of removing higher order infinitesimal terms, including when that was relative. The same used to happen in error analysis and was justified on pretty much the grounds I just gave. KF PS: I add, I am showing a trend. Let h now be 10^-200, making h^2 = 10^-40,000. The second order term is in a runaway race to the floor. We can then proceed to taking h as sufficiently infinitesimal when h^2 ~ 0. We have a quasi-definition, which also implies that H = 1/h will be quasi-infinite. It then is a reasonable next step to formalise into the hyperreals as are now more formally discussed.kairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
08:04 PM
8
08
04
PM
PDT}

To add a sliver of substance, you're still working in the real number system here, alluding to 10^-20 for example. The hyperreal numbers are very different.daveS_{April 10, 2019
April
04
Apr
10
10
2019
07:48 PM
7
07
48
PM
PDT}

DS, I used in effect the language from way back. Looking back, there was a lot that was being used intuitively and by suggestion.I am particularly noting the quasi-defining property that h^2 ~ 0. Similarly for some k of like scale to h, h*k ~ 0. And so forth. KF PS: Think of h = 10^-20. h^2 = 10^-40, which vanishes effectively in an addition of terms comparable to 10^-20, being twenty orders of magnitude down. Of course when the subtractions happen to leave a 10^-40 magnitude term as last man standing, you are in hot water.kairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
07:41 PM
7
07
41
PM
PDT}

H, I was working within the numerator, showing expansion of the binomial (x + h)^2 = x^2 + 2xh + h^2. I then reduced the higher order infinitesimal term to effective nullity per its quasi-defining property: "f(x + h) = x^2 + 2xh + h^2, and f(x) = x^2 so the difference" -- i.e. f(x + h) - f(x) -- is 2xh + h^2 ~ 2xh" yielding the final value of the numerator, an infinitesimal. I then brought in the h from the denominator in the comment "And of course 2xh/h = 2x" i.e. I cancelled the h's popping back up to the conventional number. IIRC, this was the standard first example used in Calculus texts way back. KFkairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
07:36 PM
7
07
36
PM
PDT}

KF,
DS, no. We use the property of infinitesimals that higher order terms are effectively nil (which is close to a definition!). That’s a property not a rounding. There is a difference. And BTW, this is close to the root of exchanges we had three years ago. KF
By "rounding to the nearest real number", I meant taking the standard part of the hyperreal that you obtain from the difference quotient. This has nothing to do with "higher order" terms. Here's how it goes with f(x) = x^2: (f(x + ε) - f(x))/ε = (x^2 + 2x ε + ε^2 - x^2)/ε = 2x + ε Now we take the standard part of 2x + ε which is 2x. **** Edit: From wikipedia:
In non-standard analysis, the standard part function is a function from the limited (finite) hyperreal numbers to the real numbers. Briefly, the standard part function "rounds off" a finite hyperreal to the nearest real.
daveS_{April 10, 2019
April
04
Apr
10
10
2019
07:34 PM
7
07
34
PM
PDT}

DS, no. We use the property of infinitesimals that higher order terms are effectively nil (which is close to a definition!). That's a property not a rounding. There is a difference. And BTW, this is close to the root of exchanges we had three years ago. KF PS: The vanishing of simple and mixed higher order terms is a common device in physics and economics, indeed, we can see the marginality revolution of the latter emerging. The scale of a relevant market is such that an increment of one relevant unit is effectively infinitesimal. Then also in Almagest, there is a reference I am told by which the distance to the fixed stars (the surface of the celestial sphere) is such that by comparison that of earth to sun or size of earth is effectively that of a point. In short, infinitesimals including relative ones, have been lurking in the shadows for a long time.kairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
07:26 PM
7
07
26
PM
PDT}

Re 36 I don’t know why kf left out the denominator in the definition of derivative in his P.S. in 36: if f(x) = y^2, then f’(x) = limit (as h -> 0) [(x + h)^2 - x^2] / h = [x^2 + 2xh + h^2- x^2]/h = 2x + h. So the limit is 2x as h -> 0. There isn’t any need to consider h^2. This is the very first example I used, with a picture involving the secant as kf described, when teaching students how we find derivatives and what the method means. Also, how does h is “trending infinitesimal” differ from h -> 0?hazel_{April 10, 2019
April
04
Apr
10
10
2019
07:23 PM
7
07
23
PM
PDT}

PPPS: Complete with h: https://www.siyavula.com/read/maths/grade-12/differential-calculus/06-differential-calculus-02kairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
07:18 PM
7
07
18
PM
PDT}

Hazel, Regarding #34, I haven't figured that out yet. :-)daveS_{April 10, 2019
April
04
Apr
10
10
2019
07:11 PM
7
07
11
PM
PDT}

KF, "Trending infinitesimal"? Using this nonstandard approach, you don't evaluate a limit, you just choose an infinitesimal ε and evaluate (f(x + ε) - f(x))/ε and finally "round" to the nearest real number. Edit:
I have seen a suggestion that m such that m^2 ~ 0, is a good yardstick for what an infinitesimal is.
Please let me know when you find one. :PdaveS_{April 10, 2019
April
04
Apr
10
10
2019
07:09 PM
7
07
09
PM
PDT}

Thanks, Dave. My approach is very standard, so I can't speak with any knowledge if that is what johnnby means. Any insight into my comment at 34?hazel_{April 10, 2019
April
04
Apr
10
10
2019
07:05 PM
7
07
05
PM
PDT}

Correction: I should rephrase a bit. A construction of the hyperreal numbers exists, so it's not just johnnyb assuming infinitesimals exist.daveS_{April 10, 2019
April
04
Apr
10
10
2019
07:01 PM
7
07
01
PM
PDT}

DS, he is viewing infinitesimals as hyperreals, where in effect we can have some K in *N which is greater than 0, 1, 2, . . . in "ordinary" N and gives some 1/K = m, not quite zero by way of catapult. This is then extended to the similar *R. The values of delta-x as they run in towards 0 become infinitesimal in the extremely near neighbourhood. The ratio, dy/dx, of course is a ratio and may approach a limit, where y is a function of x on the given range. The limit of [f(x + h) - f(x)]/[(x +h) - x] or even simply: [f(x + h) - f(x)]/h as h -> 0 first principles approach shows what is happening as the chord tends to the tangent and the slope therefore approaches a limit, providing it exists. The value h is of course trending infinitesimal. Where, clearly, any particular x or f(x) value is surrounded by a near-neighbourhood cloud of hyperreals, using the additivity, imported by way of extending Peano. I have seen a suggestion that m such that m^2 ~ 0, is a good yardstick for what an infinitesimal is. I don't know, but when I learned Calculus back in 4th form, that was called using first principles, likely tracing to Newton and fluxions. KF PS: let f(x) = y^2. Then f(x + h) = x^2 + 2xh + h^2, and f(x) = x^2 so the difference is 2xh + h^2 ~ 2xh. And of course 2xh/h = 2x, the "correct" value; 2xh would be an infinitesimal and we used h^2 ~ 0. Newton et al, of course, loved rendering functions into power series so extensions of polynomials allowed all sorts of results to be found. Robinson's approach and other roads to the hyperreals, etc suggest themselves. PPS: See https://revisionmaths.com/advanced-level-maths-revision/pure-maths/calculus/differentiation-first-principleskairosfocus_{April 10, 2019
April
04
Apr
10
10
2019
06:58 PM
6
06
58
PM
PDT}

hazel,
I think “infinitesimal constant” is an oxymoron. An infinitesimal means that it can get arbitrarily close to zero: dx = limit delta x as delta x -> 0. If the infinitesimal were a constant, that would mean there was a smallest number “next to 0”, and none smaller, which is exactly wrong.
I know you're responding to steve_h here, but I do think johnnyb assumes the existence of "infinitesimal constants", that is, numbers ε such that ε > 0 and yet ε < 1/n for all positive integers n. I don't know if you have commented here on such things. This strangeness is one more reason I'm skeptical about using these non-standard approaches in beginning calculus.daveS_{April 10, 2019
April
04
Apr
10
10
2019
06:34 PM
6
06
34
PM
PDT}

To Steve_h: JB addresses your question, or one like it, at the bottom of page 222. He says "However, in (5), the term d^2x/dx^2 is not itself necessarily zero, since it is not the second derivative of x with respect to x. However, he doesn't say what it is, and I don't understand his point.hazel_{April 10, 2019
April
04
Apr
10
10
2019
05:43 PM
5
05
43
PM
PDT}

I think "infinitesimal constant" is an oxymoron. An infinitesimal means that it can get arbitrarily close to zero: dx = limit delta x as delta x -> 0. If the infinitesimal were a constant, that would mean there was a smallest number "next to 0", and none smaller, which is exactly wrong. That's why you can't evaluate dy/dx by just plugging in numbers: even though both are infinitesimal, they are approaching 0 at different rates so the ratio approaches a certain number (or function, the derivative, which depends on the original function in question.). This is all covered in the basic definition of derivative, where the difference function delta y/delta x approaches a limit as delta x goes to 0. This might not be the most precise explanation possible, but it is what occurs to me off the top of my head.hazel_{April 10, 2019
April
04
Apr
10
10
2019
05:30 PM
5
05
30
PM
PDT}

It's been at least 35 years since I did any calculus and I was never any good at it, so this may be a very stupid question. If we treat dy/dx as a ratio of two functions of x and apply the quotient rule, doesn't one of your terms disappear as dx is effectively an infinitesimal constant so its derivative is zero (or to put it another way, the derivative of x with respect to x is 1, second derivative is zero)steve_h_{April 10, 2019
April
04
Apr
10
10
2019
02:58 PM
2
02
58
PM
PDT}

Prev 1 2 3 4 5 Next

You must be logged in to post a comment.

Leave a Reply