Curves often don’t do what people claim:
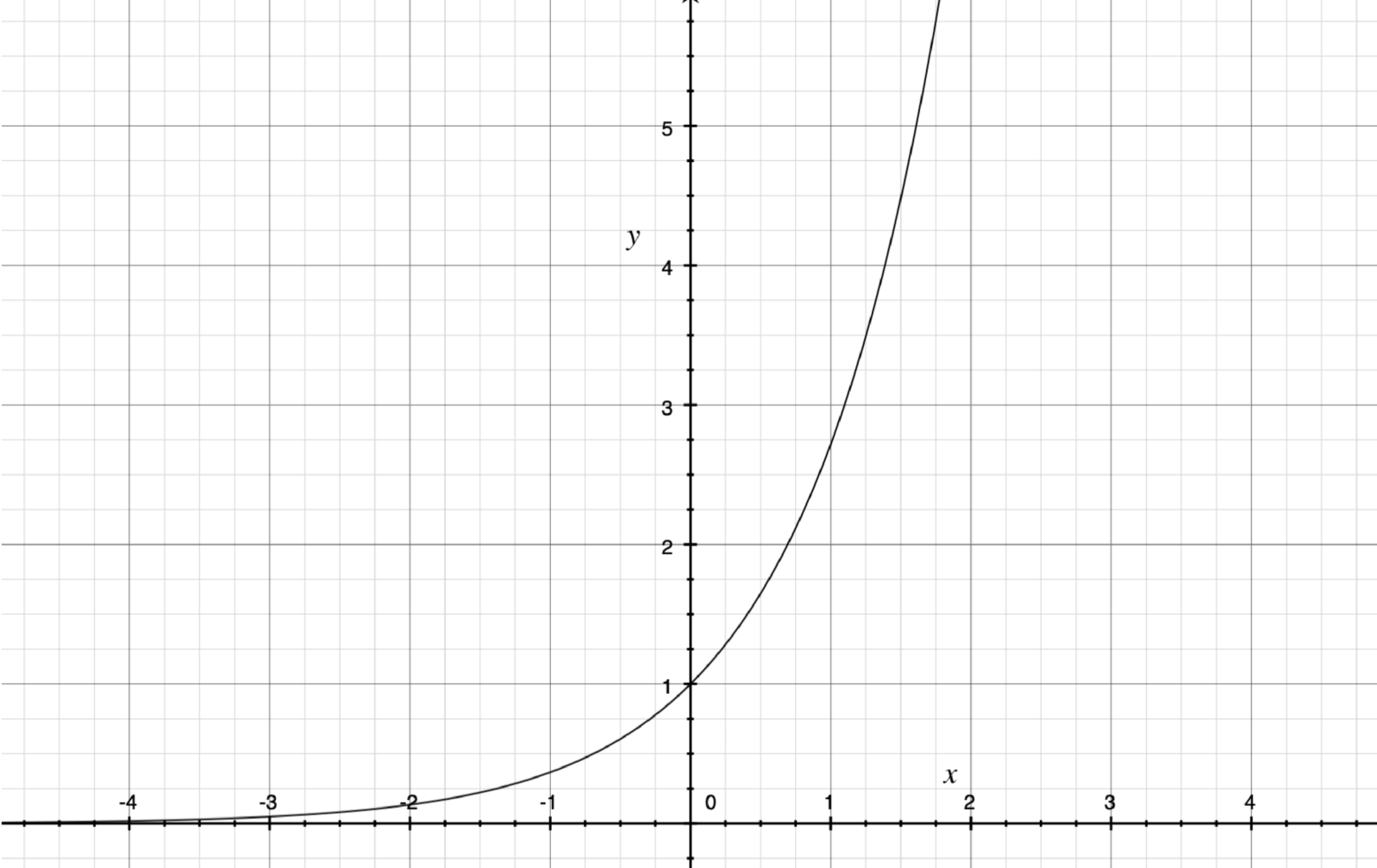
The exponential curve is one of the most powerful curves in mathematics. Notice how, on the left, the curve begins extremely flat. Then, as it progresses to the right, it gets steeper and steeper moving upward. For the most part, exponential curves occur when effects are compounded, in other words, when causes introduce effects and those effects then join up with the original causes to make a bigger cause.
While you can tell that there is a little bit of upward curve at the end, imagine if you were looking at a scatterplot of noisy data. It would be impossible to distinguish this from a straight line. It is only by knowing the causative structure of the numbers’ meaning that you can distinguish the early stage of an exponential curve from a generic position on a line. This is why bare extrapolation from data can be so dangerous—if you don’t know why the numbers are the way they are, you may be totally misinformed about the nature of the curve you are on.
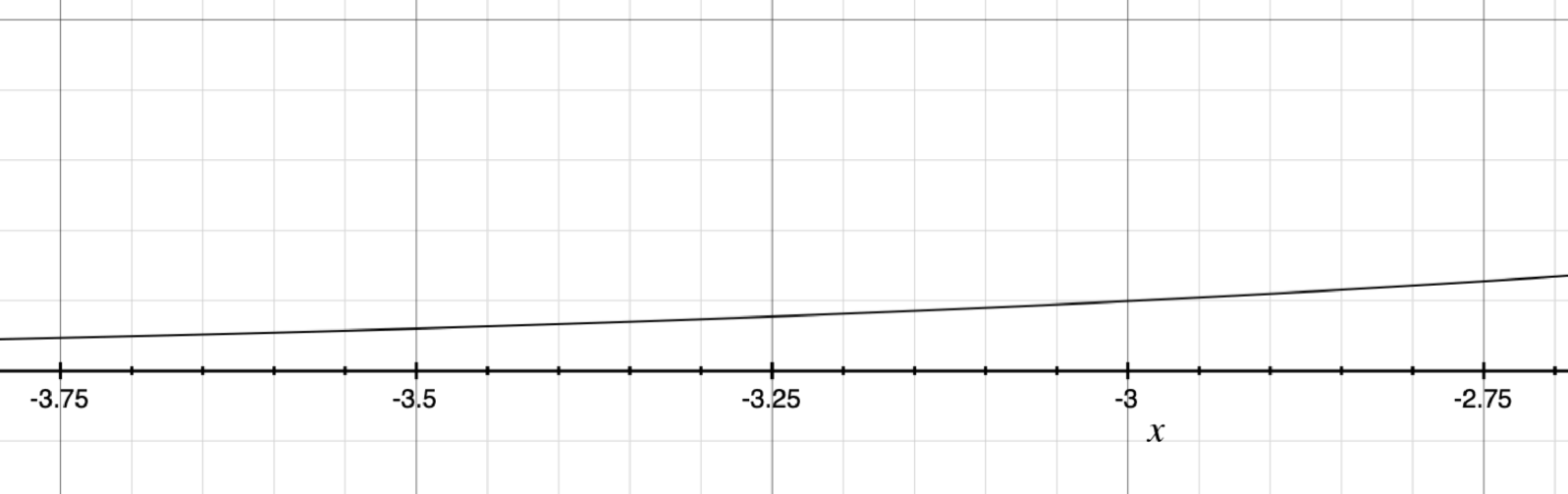
I have seen this happen with many demonstrations of evolution. Because DNA is a code, as the size of the code gets larger, the size of the search space increases exponentially. Evolution’s ability to occur within a smaller space actually gives almost no meaningful information about its ability to occur in a larger space. On the left-hand side of the curve, the effect really looks linear. But that is a trick of exponential spaces. When we trying to extrapolate the effect out to something bigger, it goes away, because the search space grows exponentially bigger.
Evolution occurs precisely when the genome can use information to restrict the search space for evolutionary targets to a manageably small size, such as when it is modifying genes to produce antibodies for foreign invaders. The cells can’t mutate randomly and achieve success, because the search space is extremely large (about three billion base pairs). Instead, the mutation space is limited to something much more manageable, just half of an existing antibody gene (the half that attached to the invader), where the search space is still large, but manageable— six hundred base pairs. The problem gets exponentially harder as the search space increases so, contrary to conventional wisdom (see also here), what works on a small scale doesn’t work on a larger scale. The exponential space prevents it. Unfortunately, people extrapolate from the front half of the curve as if it were equivalent to the entire curve.
Jonathan Bartlett, “Don’t leave home without these three curves” at Mind Matters News

Yes. An entire Darwinian evolution industry is dedicated to doing that very thing.
See also: Successful generalization is a key to learning In machine learning, the Solomonoff induction helps us decide how successful a generalization is
and
Machine learning tip: Set boundaries for the problems. We cannot take a giant pile of unorganized data, shove it into a machine, and expect useful results
Follow UD News at Twitter!