FYI-FTR: On Ehrlich’s unified overview of numbers great and small (HT: DS)

Over the past month in response to a suggestion on an infinite temporal past (and the counter argument that such is dubious), there has been quite an exchange on numbers.

In that context, it is worth headlining FYI/FTR, HT DS, a unification with continuum — oops, link —  based on surreals discussed by Ehrlich:

where also:

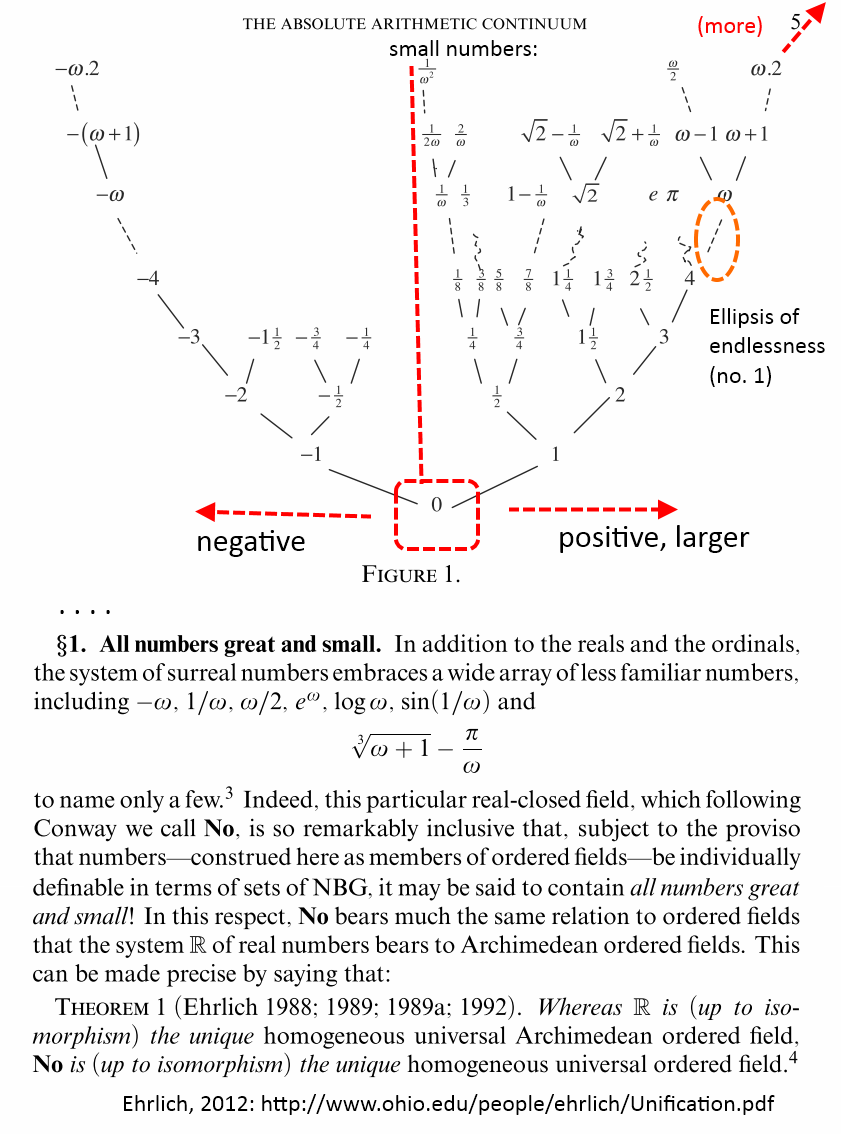
Such of course provides a lot of breathing room for exploring numbers and relationships in a unified context. Attention is particularly drawn to various ellipses of endlessness (not able to be traversed in finite stage stepwise do forever processes) and to both the trans-finites . . . do not overlook ellipses of endlessness within transfinite ranges — and the infinitesimals including what we could call a particularly mild one, 1/omega. (Cf therefore the previously suggested 1/m –> A = omega + g, g a large but finite number.)

Looks like the numbers sandbox is now officially open for play.

There being a live thread, comments may be entertained here on. END

PS: Let me clip Wolfram on ordinals, drawing out that rightmost branch a bit:

PPS: Let me clip from a comment today Mar 1 on Ax Inf:

>>546 kairosfocus March 1, 2016 at 8:48 am

PS: For convenience Wiki on Ax inf:

“In words, there is a set I (the set which is postulated to be infinite), such that the empty set is in I and such that whenever any x is a member of I, the set formed by taking the union of x with its singleton {x} is also a member of I. Such a set is sometimes called an inductive set.

Interpretation and consequences

This axiom is closely related to the von Neumann construction of the naturals in set theory, in which the successor of x is defined as x U {x}. If x is a set, then it follows from the other axioms of set theory that this successor is also a uniquely defined set. Successors are used to define the usual set-theoretic encoding of the natural numbers. In this encoding, zero is the empty set:

0 = {}.

The number 1 is the successor of 0:

1 = 0 U {0} = {} U {0} = {0}.

Likewise, 2 is the successor of 1:

2 = 1 U {1} = {0} U {1} = {0,1},

and so on. A consequence of this definition is that every natural number is equal to the set of all preceding natural numbers.

[–> the copy set to date principle highlighted in 217 above; this is where my concern that were N to be all finite values but extends endlessly, at some point it would need endless members. Of course — like the ever receding foot of the rainbow — that cannot be reached and so we have the ellipsis as a crucial part of N, i.e. we may only actually operationally succeed to finite values but may do so without upper limit. The endlessness of first order is then transferred to its order type w]

This construction forms the natural numbers. However, the other axioms are insufficient to prove the existence of the set of all natural numbers. Therefore its existence is taken as an axiom—the axiom of infinity. [–> forcing the result by pointing across the ellipsis of endlessness] This axiom asserts that there is a set I that contains 0 and is closed under the operation of taking the successor [–> which is endless in principle but operationally is ever limited to finite and bounded individual values]; that is, for each element of I, the successor of that element is also in I.

Thus the essence of the axiom is:

There is a set, I, that includes all the natural numbers.”

[–> which becomes endless in principle though operationally we may only succeed to finite specific values and as the pink/ blue paper tape thought exercise

shows, for every k of arbitrarily large but finite scale we can truncate the [blue] tape [drawn in to that point] so far and [then] set k to correspond to 0 in the unmoved pink tape, k+1 to 1, etc and obtain an endless 1:1 match,

that is, endlessness is pivotal and cannot be traversed stepwise [–> I add, recursively, we do so by a leap of faith, a pointing across the ellipsis of endlessness which we embed in our axioms]]>>