Logic & First Principles 8: Bridging the Wigner MATH-PHYSICS GAP (with help from phase/ configuration/ state space)

_{kairosfocus

January 22, 2019

Logic and Reason, Mathematics, Physics}

Share: Facebook; Twitter; LinkedIn; Flipboard; Print; Email

In order to conceptually bridge the Wigner MATH-PHYSICS GAP, it is helpful to see how deeply embedded quantitative and structural properties are in the physical world. The phase space approach is helpful, and a vid on how colliding blocks compute digits of pi (under ideal circumstances) will help. The vid:

It helps to look at some screenshots:

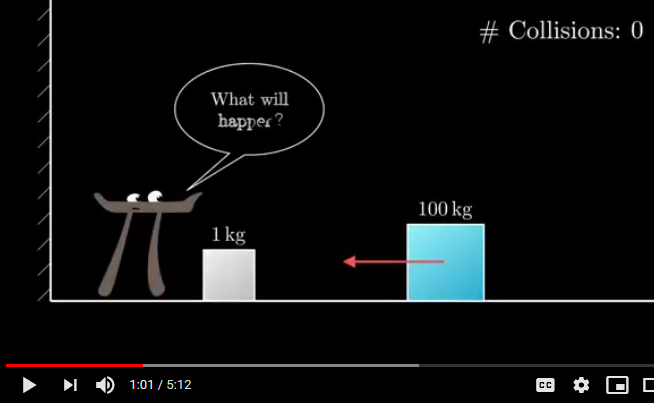
In this first shot (from a part 1 vid) we see a setup where we have a frictionless plane with a rigid wall to the left and two masses that collide. On the first hitting the second, it will hit and bounce back (elastically) from the wall. A second collision with the first block follows and rebound from the wall. This will continue until the second block cannot catch up with the first. Amazingly, depending on the mass ratio, the number of collisions between blocks or with the wall will give digits of pi.

Such suggests that there is a hidden circle, and there is, in an associated phase space — which allows us to see the dynamics from a geometric viewpoint in an associated abstract space:

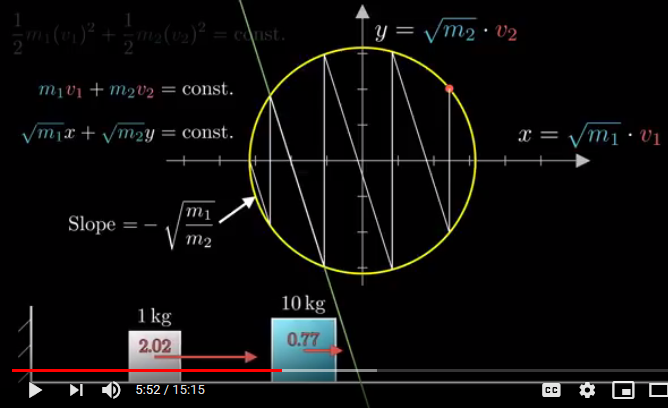
Here, we see blocks moving so that kinetic energy and momentum are conserved. The circle shows constant kinetic energy and the zigzag jumps come from momentum conservation during collision — the vertical one being due to collisions with the wall of effectively infinite mass (rigidity). Due to collisions, they are switching directions and points on the circle on collisions. And, the angle at the centre will be twice that at the circumference standing on the same arc, here marking three successive collisions:

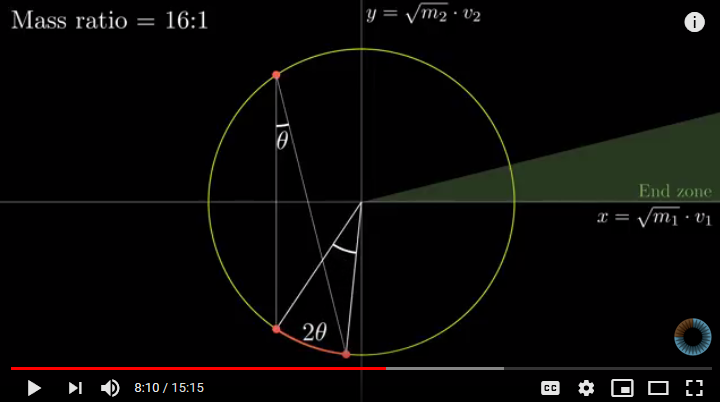
This continues until a critical value is left. It turns out, that this is when the arc-jump around the circle can no longer achieve a critical value:

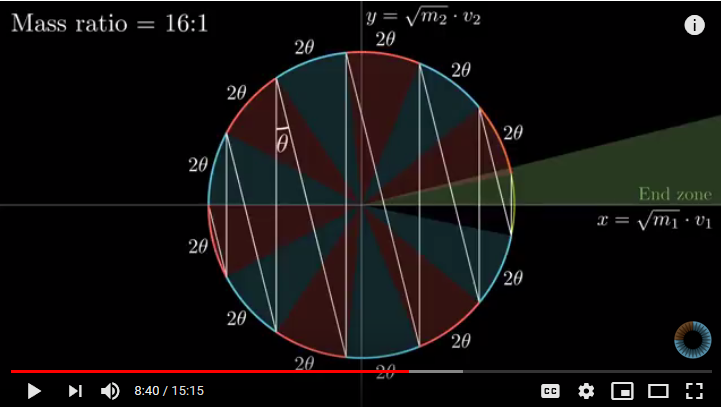
The result of all this is that we move, depending on mass ratio, from 3 to 31 to 314 collisions and onward. Which computes pi’s digits.

Of course, we have idealised the system to be friction-free. (In the video, clacks are added as an audio effect, with energy conservation there would obviously be no noise.)

We see here how a physical situation (admittedly idealised) obeys laws of physics which were empirically discovered. These reveal a deeply embedded logic of structure and quantity manifest in phenomena of the world. Where, we may freely move to an abstract, phase space which allows further insight and analysis.

In this case, geometry counts.

Counts to the point that an idealised case would allow computation of digits of pi.

Of course, we could not actually build such a system, but the laws we infer from the observed world help us to form abstract model logic worlds that give us insights and which often help us to understand real world cases with friction etc.

Why all of this is possible is because the physical world is governed by logic of being constraints that are structural and quantitative. Laws, that turn out in aggregate to be fine tuned in ways that enable C-Chemistry, aqueous medium, cell based life. END

PS: Mobius strip cutting exercise:

https://www.youtube.com/watch?v=gXsgkojxkdY

Comments

Math Guy your post on the circular argument that is found within quantum mechanics when holding that mathematics is 'merely' a by-product of human evolution, reminded me of this article by Steven Weinberg entitled "The Trouble with Quantum Mechanics" in which he stated, "the instrumentalist approach turns its back on a vision that became possible after Darwin, of a world governed by impersonal physical laws that control human behavior along with everything else. It is not that we object to thinking about humans. Rather, we want to understand the relation of humans to nature, not just assuming the character of this relation by incorporating it in what we suppose are nature’s fundamental laws, but rather by deduction from laws that make no explicit reference to humans."
The Trouble with Quantum Mechanics – Steven Weinberg – JANUARY 19, 2017 Today there are two widely followed approaches to quantum mechanics, the “realist” and “instrumentalist” approaches, which view the origin of probability in measurement in two very different ways.9 ,,, In the instrumentalist approach,,, humans are brought into the laws of nature at the most fundamental level.,,, the instrumentalist approach turns its back on a vision that became possible after Darwin, of a world governed by impersonal physical laws that control human behavior along with everything else. It is not that we object to thinking about humans. Rather, we want to understand the relation of humans to nature, not just assuming the character of this relation by incorporating it in what we suppose are nature’s fundamental laws, but rather by deduction from laws that make no explicit reference to humans.,,, In quantum mechanics these probabilities do not exist until people choose what to measure, such as the spin in one or another direction. Unlike the case of classical physics, a choice must be made,,,, http://quantum.phys.unm.edu/466-17/QuantumMechanicsWeinberg.pdf
This is simply devastating to the atheistic worldview on so many levels. Steven Weinberg, an atheist, rejected the instrumentalist approach in quantum mechanics precisely because it undermines the Darwinian worldview from within since "humans are brought into the laws of nature at the most fundamental level". But, regardless of Weinberg's a-priori atheistic bias against the reality of Agent causality and/or free will within quantum mechanics, the 'free will loophole' has now been, for all practical purposes, experimentally closed. That is to say that advances in quantum mechanics itself now demands that agent causality and/or free will be let into physics. In regards to the Kochen-Speckter Theorem we find, as leading experimental physicist Anton Zeilinger states in the following video, what we perceive as reality now depends on our earlier decision what to measure. Which is a very, very, deep message about the nature of reality and our part in the whole universe. We are not just passive observers.”
“The Kochen-Speckter Theorem talks about properties of one system only. So we know that we cannot assume – to put it precisely, we know that it is wrong to assume that the features of a system, which we observe in a measurement exist prior to measurement. Not always. I mean in a certain cases. So in a sense, what we perceive as reality now depends on our earlier decision what to measure. Which is a very, very, deep message about the nature of reality and our part in the whole universe. We are not just passive observers.” Anton Zeilinger – Quantum Physics Debunks Materialism – video (7:17 minute mark) https://www.youtube.com/watch?feature=player_detailpage&v=4C5pq7W5yRM#t=437
And with contextuality we find, “In the quantum world, the property that you discover through measurement is not the property that the system actually had prior to the measurement process. What you observe necessarily depends on how you carried out the observation” and “Measurement outcomes depend on all the other measurements that are performed – the full context of the experiment. Contextuality means that quantum measurements can not be thought of as simply revealing some pre-existing properties of the system under study. ”
Contextuality is ‘magic ingredient’ for quantum computing – June 11, 2012 Excerpt: Contextuality was first recognized as a feature of quantum theory almost 50 years ago. The theory showed that it was impossible to explain measurements on quantum systems in the same way as classical systems. In the classical world, measurements simply reveal properties that the system had, such as colour, prior to the measurement. In the quantum world, the property that you discover through measurement is not the property that the system actually had prior to the measurement process. What you observe necessarily depends on how you carried out the observation. Imagine turning over a playing card. It will be either a red suit or a black suit – a two-outcome measurement. Now imagine nine playing cards laid out in a grid with three rows and three columns. Quantum mechanics predicts something that seems contradictory – there must be an even number of red cards in every row and an odd number of red cards in every column. Try to draw a grid that obeys these rules and you will find it impossible. It’s because quantum measurements cannot be interpreted as merely revealing a pre-existing property in the same way that flipping a card reveals a red or black suit. Measurement outcomes depend on all the other measurements that are performed – the full context of the experiment. Contextuality means that quantum measurements can not be thought of as simply revealing some pre-existing properties of the system under study. That’s part of the weirdness of quantum mechanics. http://phys.org/news/2014-06-weird-magic-ingredient-quantum.html
Moreover, the final ‘free will’ loophole in quantum mechanics has now been closed. As the following article states, the “creepy” and “far-fetched” possibility that the “physicist running the experiment does not have complete free will in choosing each detector’s setting” and that “a particle detector’s settings may “conspire” with events in the shared causal past of the detectors themselves to determine which properties of the particle to measure”,,,
Closing the ‘free will’ loophole: Using distant quasars to test Bell’s theorem – February 20, 2014 Excerpt: Though two major loopholes have since been closed, a third remains; physicists refer to it as “setting independence,” or more provocatively, “free will.” This loophole proposes that a particle detector’s settings may “conspire” with events in the shared causal past of the detectors themselves to determine which properties of the particle to measure — a scenario that, however far-fetched, implies that a physicist running the experiment does not have complete free will in choosing each detector’s setting. Such a scenario would result in biased measurements, suggesting that two particles are correlated more than they actually are, and giving more weight to quantum mechanics than classical physics. “It sounds creepy, but people realized that’s a logical possibility that hasn’t been closed yet,” says MIT’s David Kaiser, the Germeshausen Professor of the History of Science and senior lecturer in the Department of Physics. “Before we make the leap to say the equations of quantum theory tell us the world is inescapably crazy and bizarre, have we closed every conceivable logical loophole, even if they may not seem plausible in the world we know today?” https://www.sciencedaily.com/releases/2014/02/140220112515.htm
,,, that “creepy” and “far-fetched” possibility, (which is exactly the “creepy” and “far-fetched” possibility that atheists hold to be true), has now been, for all practical purposes, closed. Anton Zeilinger and company have now pushed the “free-will loophole” back to 7.8 billion years ago using quasars to determine measurement settings.
Cosmic Bell Test Using Random Measurement Settings from High-Redshift Quasars – Anton Zeilinger – 14 June 2018 Abstract: In this Letter, we present a cosmic Bell experiment with polarization-entangled photons, in which measurement settings were determined based on real-time measurements of the wavelength of photons from high-redshift quasars, whose light was emitted billions of years ago; the experiment simultaneously ensures locality. Assuming fair sampling for all detected photons and that the wavelength of the quasar photons had not been selectively altered or previewed between emission and detection, we observe statistically significant violation of Bell’s inequality by 9.3 standard deviations, corresponding to an estimated p value of ? 7.4 × 10^21. This experiment pushes back to at least ? 7.8 Gyr ago the most recent time by which any local-realist influences could have exploited the “freedom-of-choice” loophole to engineer the observed Bell violation, excluding any such mechanism from 96% of the space-time volume of the past light cone of our experiment, extending from the big bang to today. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.080403
Moreover, here is another recent interesting experiment by Anton Zeilinger, (and about 70 other researchers), that insured the complete independence of measurement settings in a Bell test from the free will choices of 100,000 human participants instead of having a physical randomizer determine measurement settings.
Challenging local realism with human choices – A. Zeilinger – 20 May 2018 Abstract: A Bell test, which challenges the philosophical worldview of local realism against experimental observations, is a randomized trial requiring spatially-distributed entanglement, fast and high-efficiency detection, and unpredictable measurement settings. While technology can perfect the first two of these, and while technological randomness sources enable device-independent protocols based on Bell inequality violation, challenging local realism using physical randomizers inevitably makes assumptions about the same physics one aims to test. Bell himself noted this weakness of physical setting choices and argued that human free will could rigorously be used to assure unpredictability in Bell tests. Here we report a suite of local realism tests using human choices, avoiding assumptions about predictability in physics. We recruited ~100,000 human participants to play an online video game that incentivizes fast, sustained input of unpredictable bits while also illustrating Bell test methodology. The participants generated 97,347,490 binary choices, which were directed via a scalable web platform to twelve laboratories on five continents, in which 13 experiments tested local realism using photons, single atoms, atomic ensembles, and superconducting devices. Over a 12-hour period on the 30 Nov. 2016, participants worldwide provided a sustained flow of over 1000 bits/s to the experiments, which used different human-generated bits to choose each measurement setting. The observed correlations strongly contradict local realism and other realist positions in bi-partite and tri-partite scenarios. Project outcomes include closing of the freedom-of-choice loophole, gamification of statistical and quantum non-locality concepts, new methods for quantum-secured communications, a very large dataset of human-generated randomness, and networking techniques for global participation in experimental science. https://arxiv.org/abs/1805.04431
Again, this is devastating to the atheistic worldview on so many levels. Bringing humans "into the laws of nature at the most fundamental level" has some fairly profound implications. First, by allowing Agent Causality of God (and ourselves) back into the picture of modern physics, as quantum physics itself now demands, and as the Christian founders of modern physics originally envisioned, (Sir Isaac Newton, James Clerk Maxwell, Michael Faraday, and Max Planck, to name a few), then a empirically backed reconciliation, (via the Shroud of Turin), between Quantum Mechanics and General Relativity, i.e. the ‘Theory of Everything’, readily pops out for us in Christ’s resurrection from the dead.
Short take: Copernican Principle, Agent Causality, and Jesus Christ as the “Theory of Everything” - January 22, 2019 Copernican Principle https://uncommondesc.wpengine.com/intelligent-design/bill-nye-should-check-wikipedia/#comment-671672 Agent Causality https://uncommondesc.wpengine.com/intelligent-design/bill-nye-should-check-wikipedia/#comment-671692
And secondly, besides the reality of ‘free will’ and/or Agent causality within quantum theory bringing that rather startling solution to the much sought after ‘theory of everything’, there is also another fairly drastic implication for individual people being “brought into the laws of nature at the most fundamental level' (S. Weinberg)” as well. Although free will is often thought of as allowing someone to choose between a veritable infinity of options, in a theistic view of reality that veritable infinity of options all boils down to just two options. Eternal life, (infinity if you will), with God, or Eternal life, (infinity again if you will), without God. And exactly as would be a priori expected on the Christian view of reality, we find two very different eternities in reality. An ‘infinitely destructive’ eternity associated with General Relativity and a extremely orderly eternity associated with Special Relativity:
Quantum Mechanics, Special Relativity, General Relativity and Christianity – video https://www.youtube.com/watch?v=h4QDy1Soolo How Special Was The Big Bang? “But why was the big bang so precisely organized (to 1 in 10^10^123), whereas the big crunch (or the singularities in black holes) would be expected to be totally chaotic? It would appear that this question can be phrased in terms of the behaviour of the WEYL part of the space-time curvature at space-time singularities. What we appear to find is that there is a constraint WEYL = 0 (or something very like this) at initial space-time singularities-but not at final singularities-and this seems to be what confines the Creator’s choice to this very tiny region of phase space.” Roger Penrose – (from the Emperor’s New Mind, Penrose, pp 339-345 copyright 1989, Penguin Books) “Einstein’s equation predicts that, as the astronaut reaches the singularity (of the black-hole), the tidal forces grow infinitely strong, and their chaotic oscillations become infinitely rapid. The astronaut dies and the atoms which his body is made become infinitely and chaotically distorted and mixed-and then, at the moment when everything becomes infinite (the tidal strengths, the oscillation frequencies, the distortions, and the mixing), spacetime ceases to exist.” Kip S. Thorne – “Black Holes and Time Warps: Einstein’s Outrageous Legacy” pg. 476
Verses:
Colossians 1:15-20 The Son is the image of the invisible God, the firstborn over all creation. For in him all things were created: things in heaven and on earth, visible and invisible, whether thrones or powers or rulers or authorities; all things have been created through him and for him. He is before all things, and in him all things hold together. And he is the head of the body, the church; he is the beginning and the firstborn from among the dead, so that in everything he might have the supremacy. For God was pleased to have all his fullness dwell in him, and through him to reconcile to himself all things, whether things on earth or things in heaven, by making peace through his blood, shed on the cross.
bornagain77

MG, I think I am reduced to pondering peculiarities of paper loops and cutting along the loop [having given several less direct illustrative cases]. Where, a twist and whether you cut centrally or close enough to one side can make a big difference. Last I checked, paper loops, a pair of scissors and a spot of glue or tape were not figments of anyone's imagination, nor are their properties sensitive to our axiomatisations, philosophies, contemplations, etc. We are talking about bodies in space with the interesting result of having one surface due to the twist. So far as I can see, the Mobius strip is a direct demonstration of embedded structural and quantitative phenomena in our world, here tied to space and to bodies in space. With that in hand, we can go back and re-think, seeing how certain core math facts, properties, entities lock into the distinct identity needed to set up any particular possible world, and how many consequences flow from that. KF kairosfocus

The following observation is found in Omne's book Quantum Philosophy. Assuming that mathematics is a by-product of human evolution gives a circular argument, that goes like this: 1) Humans evolve mathematical ability over time. We invent ever deeper math structures and objects to explain natural phenomena. 2) During the 20th century we learn about Hilbert spaces (the math underlying quantum physics). 3) We find that all matter obeys the mathematical laws of quantum mechanics, including our own brains! 4) So the abstract math we "invent" to study the world already exists in the subatomic structure of the (supposedly solely material) brains that are doing the "inventing"! math guy

PS: Should I note that two properties, permeability and permitivity of free space were measured and then were found working together as a wave velocity suspiciously close to the speed of light. kairosfocus

H, start by taking a sheet of paper, loop with a twist and cut around the loop in the middle. Set up a second, and cut at 1/3 width. Notice the difference. I think the structural and quantitative properties revealed cannot be in our minds, it is paper in our hands here. Paper, in space, with certain form factor. Other than when the paper is arranged in space in this way, it will not behave like that. Space, an aspect of our world, has properties in it -- embedded if you will -- that manifest in this way, exhibiting structural and quantitative features. This is an empirical demonstration and on a scale that makes it a property of a 3-d spatial domain; here manifest to moral certainty (what empirical observation delivers). Similarly, the distinctness for any particular possible world entails the natural numbers as embedded, with further things associated. Whether you agree or object is at this point immaterial, as you have no warrant to the contrary. Especially when the root premises are inescapable first principles such as distinct identity. KF kairosfocus

hazel:
It’s the ” properties are embedded” part that I am arguing against as certain.
Denying isn't arguing. If not a “happy coincidence”, then what (if math was invented by us)? What is your positive case and supporting evidence? ET

It's the " properties are embedded" part that I am arguing against as certain. You don't seem to be able to sort out what we do and don't agree about. hazel

H, then you have the evidence figuratively in hand. If that does not make it patent to you that structural, quantitative, rationally intelligible properties are embedded in space and in bodies in space, independent of our views, perceptions, claims or arguments, then no degree of warrant will. KF kairosfocus

I know how Mobius strips work, kf. hazel

H, that is truly sad. I simply ask you to set up two Mobius strips and an ordinary loop of paper then proceed to cut one strip and the loop in half, going around the loop. Then, cut the other M-strip at the 1/3 across point. For the first M-strip, cut it in the middle a second time. Ponder on how the results are plainly independent of what you or any other human being cares to think, but are readily confirmed by doing the experiment oneself. Then, please think again on whether rationally intelligible properties of structure and quantity are or are not to be found in space and in bodies in space, embedded in ways that must go to the roots of reality. KF kairosfocus

kf writes,
so they have locked themselves out of the circle of evidence-responsive discussion.. KF
So be it: I stand "locked out". :-) hazel

Folks, let us go get some paper, glue or tape and scissors, or at least watch the Mobius strip in action. If that does not demonstrate to our satisfaction how structure and quantity are embedded in space and figures in space, nothing will. And further to all this if Matrhematical, logical and directly observable empirical demonstrations meet with such a wall of objections on what should not be controversial, then that tells us utter volumes on why evidence of signs of design meet with similar walls of unyielding objection. The time has come to stand non our epistemic rights, pointing to how insistent objectors are utterly unresponsive to essentially any degree of warrant so they have locked themselves out of the circle of evidence-responsive discussion.. KF kairosfocus

If you have something other than the infinite Mind of God that can ground 'platonically perfect' mathematics, then by all means clearly lay it out. Please do be explicit in your definitions and don't hide in a haze Hazel. My case for the infinite Mind of God grounding mathematics is laid out in posts 13-17, and is certainly clear for all fair minded readers to see. bornagain77

hazel- then correct bornagain77 instead of just denying what he said. That would go a long way to support your claim of "That is not what I think." If not a "happy coincidence", then what (if math was invented by us)? ET

Bornagain writes,
Basically Hazel is arguing that the applicability of mathematics to the physical world, no matter how uncanny and accurate it may be, is just a ‘happy coincidence’ that needs no further explanation
That is not what I think. Please don't put words in my mouth. hazel

kf, you are wasting your time posting all these examples. We all know that math can describe the world, and that modeling relationships between pure math and actual events in the physical world exist, and that there is a mystery, in Wigner's words, as to the unreasonable effectiveness of this relationship. The only issue that I am addressing is your claim that the abstractions which exist in our minds as parts of pure math are embedded in the physical world. I am claiming that another way to look at it is that the physical world contains physical things which behave in certain ways that can be described by our mathematical abstractions, but those abstractions don't themselves exist in the physical world. This is a philosophical point of view, and your position is also. Your Platonic premise that the abstractions exist antecedent to the physical world, are embedded in it, and constrain it may be true, but it is not demonstrably true. Other premises lead to different conclusions, and may also be true. The history of philosophy shows clearly that there is no definitive way to resolve this issue. So no further amount of examples of neat math and neat examples in the physical world will add any more weight to your perspective. hazel

Simply put, in order to adequately explain quantum wave collapse we must postulate something with the causal sufficiency within itself in order to explain the ‘effect’ of the ‘infinite dimensional-infinite information’ quantum wave state collapsing to a single bit of information. In other words, we must postulate the omnipresent and omniscient Mind of God in order to explain why the ‘infinite dimensional-infinite information’ quantum wave state collapses to a single bit of information. Moreover, with the refutation of hidden variables, there is no cause that materialists can possibly appeal to in order to 'explain away' this 'timeless activity' that is constantly witnessed in quantum mechanics. As the following article states, “Our result gives weight to the idea that quantum correlations somehow arise from outside spacetime, in the sense that no story in space and time can describe them,”
Looking beyond space and time to cope with quantum theory – 29 October 2012 Excerpt: “Our result gives weight to the idea that quantum correlations somehow arise from outside spacetime, in the sense that no story in space and time can describe them,” http://www.quantumlah.org/highlight/121029_hidden_influences.php
Whereas, on the other hand, I, as a Christian, have a beyond space and time cause that I can readily appeal to in order to explain the timeless effects of quantum mechanics:
Colossians 1:17 He is before all things, and in Him all things hold together.
Thus in conclusion, the ‘idealized situation’ of platonic perfection is reached to its highest ‘insane’ degree in quantum mechanics, and this ‘idealized situation’ of platonic perfection being reached in Quantum Mechanics gives every indication of being reached by none other than the infinite Mind of God. There simply is no other postulated cause by atheists that is remotely capable of explaining what we see in Quantum Mechanics (which is, by far, our most accurate and foundational mathematical model of reality). Supplemental note:
Quantum Mechanics, Special Relativity, General Relativity and Christianity - video https://www.youtube.com/watch?v=h4QDy1Soolo
bornagain77

To give a glimpse of just how insanely precise the measurement of 120 standard deviations is for Leggett's Inequality in Quantum Mechanics,,,
Standard deviation Excerpt: In statistics, the standard deviation (SD) (represented by the Greek letter sigma, ?),,, Particle physics uses a standard of "5 sigma" for the declaration of a discovery.[3] At five-sigma there is only one chance in nearly two million that a random fluctuation would yield the result. http://en.wikipedia.org/wiki/Standard_deviation#Particle_physics SSDD: a 22 sigma event is consistent with the physics of fair coins? - June 23, 2013 Excerpt: So 500 coins heads is (500-250)/11 = 22 standard deviations (22 sigma) from expectation! These numbers are so extreme, it’s probably inappropriate to even use the normal distribution’s approximation of the binomial distribution, and hence “22 sigma” just becomes a figure of speech in this extreme case… https://uncommondesc.wpengine.com/mathematics/ssdd-a-22-sigma-event-is-consistent-with-the-physics-of-fair-coins/
And again, as far as our best scientific instruments will allow us to measure, we can find no deviation whatsoever from what the 'platonically perfect' mathematical theories of Special Relativity, General Relativity, Quantum-Electrodynamics, and Quantum Mechanics predict. In regards to the ‘platonic perfection’ revealed by Quantum Mechanics in particular, Heisenberg stated,,,
“I think that modern physics has definitely decided in favor of Plato. In fact the smallest units of matter are not physical objects in the ordinary sense; they are forms, ideas which can be expressed unambiguously only in mathematical language.” - Werner Heisenberg
In regards to further establishing that the Mind of God is behind the insanely precise 120 standard deviation ‘platonic perfection’ of Quantum Mechanics, it is interesting to note Quantum Mechanics is more foundational to our description of reality than either Special Relativity and General Relativity are. As Vlatko Vedral states, “space and time are two of the most fundamental classical concepts, but according to quantum mechanics they are secondary.,,, We must explain space and time (4D space-time) as somehow emerging from fundamentally spaceless and timeless physics.”
LIVING IN A QUANTUM WORLD – Vlatko Vedral – 2011 Excerpt: Thus, the fact that quantum mechanics applies on all scales forces us to confront the theory’s deepest mysteries. We cannot simply write them off as mere details that matter only on the very smallest scales. For instance, space and time are two of the most fundamental classical concepts, but according to quantum mechanics they are secondary. The entanglements are primary. They interconnect quantum systems without reference to space and time. If there were a dividing line between the quantum and the classical worlds, we could use the space and time of the classical world to provide a framework for describing quantum processes. But without such a dividing line—and, indeed, without a truly classical world—we lose this framework. We must explain space and time (4D space-time) as somehow emerging from fundamentally spaceless and timeless physics. http://phy.ntnu.edu.tw/~chchang/Notes10b/0611038.pdf
And indeed, to further back of the claim that the Mind of God is behind the ‘platonic perfection’ of Quantum Mechanics, ‘the experience of the now’, which is a defining attribute of the immaterial mind, (and which corresponds to to the 'timelessness' of the platonic realm), is found to have a consistent correspondence to quantum mechanics no matter how we might choose to perform our measurements in Quantum Mechanics:
Albert Einstein vs. Quantum Mechanics and His Own Mind – video https://www.youtube.com/watch?v=vxFFtZ301j4
As Professor Scott Aaronson quipped, “Look, we all have fun ridiculing the creationists,,, But if we accept the usual picture of quantum mechanics, then in a certain sense the situation is far worse: the world (as you experience it) might as well not have existed 10^-43 seconds ago!”
“Look, we all have fun ridiculing the creationists who think the world sprang into existence on October 23, 4004 BC at 9AM (presumably Babylonian time), with the fossils already in the ground, light from distant stars heading toward us, etc. But if we accept the usual picture of quantum mechanics, then in a certain sense the situation is far worse: the world (as you experience it) might as well not have existed 10^-43 seconds ago!” – Scott Aaronson – MIT associate Professor quantum computation - Lecture 11: Decoherence and Hidden Variables
And to further back up the claim that the Mind of God is behind the insanely precise 120 standard deviation ‘platonic perfection’ of Quantum Mechanics, the quantum wave, prior to measurement, is mathematically defined as being in a ‘infinite dimensional-infinite information’ state,
The Unreasonable Effectiveness of Mathematics in the Natural Sciences – Eugene Wigner – 1960 Excerpt: We now have, in physics, two theories of great power and interest: the theory of quantum phenomena and the theory of relativity.,,, The two theories operate with different mathematical concepts: the four dimensional Riemann space and the infinite dimensional Hilbert space, http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html Wave function Excerpt “wave functions form an abstract vector space”,,, This vector space is infinite-dimensional, because there is no finite set of functions which can be added together in various combinations to create every possible function. http://en.wikipedia.org/wiki/Wave_function#Wave_functions_as_an_abstract_vector_space Explaining Information Transfer in Quantum Teleportation: Armond Duwell †‡ University of Pittsburgh Excerpt: In contrast to a classical bit, the description of a (quantum) qubit requires an infinite amount of information. The amount of information is infinite because two real numbers are required in the expansion of the state vector of a two state quantum system (Jozsa 1997, 1) http://www.cas.umt.edu/phil/faculty/duwell/DuwellPSA2K.pdf Quantum Computing – Stanford Encyclopedia Excerpt: Theoretically, a single qubit can store an infinite amount of information, yet when measured (and thus collapsing the superposition of the Quantum Wave state) it yields only the classical result (0 or 1),,, http://plato.stanford.edu/entries/qt-quantcomp/#2.1 WHAT SCIENTIFIC IDEA IS READY FOR RETIREMENT? Infinity – Max Tegmark Excerpt: real numbers with their infinitely many decimals have infested almost every nook and cranny of physics, from the strengths of electromagnetic fields to the wave functions of quantum mechanics: we describe even a single bit of quantum information (a qubit) using two real numbers involving infinitely many decimals. https://www.edge.org/response-detail/25344
bornagain77

That is to say, the place where “platonic perfection” is, not only approached, but, (as far as our best scientific measurements will allow us to see), ‘perfectly reached’ in the universe, is for the ‘flatness’ of the universe.
How do we know the universe is flat? Discovering the topology of the universe – by Fraser Cain – June 7, 2017 Excerpt: With the most sensitive space-based telescopes they have available, astronomers are able to detect tiny variations in the temperature of this background radiation. And here’s the part that blows my mind every time I think about it. These tiny temperature variations correspond to the largest scale structures of the observable universe. A region that was a fraction of a degree warmer become a vast galaxy cluster, hundreds of millions of light-years across. The cosmic microwave background radiation just gives and gives, and when it comes to figuring out the topology of the universe, it has the answer we need. If the universe was curved in any way, these temperature variations would appear distorted compared to the actual size that we see these structures today. But they’re not. To best of its ability, ESA’s Planck space telescope, can’t detect any distortion at all. The universe is flat.,,, We say that the universe is flat, and this means that parallel lines will always remain parallel. 90-degree turns behave as true 90-degree turns, and everything makes sense.,,, Since the universe is flat now, it must have been flat in the past, when the universe was an incredibly dense singularity. And for it to maintain this level of flatness over 13.8 billion years of expansion, in kind of amazing. In fact, astronomers estimate that the universe must have been flat to 1 part within 1×10^57 parts. Which seems like an insane coincidence. https://phys.org/news/2017-06-universe-flat-topology.html
Moreover, this ‘insane coincidence’ of ‘platonic perfection’ being reached for the axiomatic ‘primitive object’ of the line just so happens to be necessary for us to even be able to practice math and science, (and apply technology in our world), in the first place:
How do we know the universe is flat? Discovering the topology of the universe – by Fraser Cain – June 7, 2017 Excerpt: We say that the universe is flat, and this means that parallel lines will always remain parallel. 90-degree turns behave as true 90-degree turns, and everything makes sense.,,, https://phys.org/news/2017-06-universe-flat-topology.html Why We Need Cosmic Inflation By Paul Sutter, Astrophysicist | October 22, 2018 Excerpt: As best as we can measure, the geometry of our universe appears to be perfectly, totally, ever-so-boringly flat. On large, cosmic scales, parallel lines stay parallel forever, interior angles of triangles add up to 180 degrees, and so on. All the rules of Euclidean geometry that you learned in high school apply. But there’s no reason for our universe to be flat. At large scales it could’ve had any old curvature it wanted. Our cosmos could’ve been shaped like a giant, multidimensional beach ball, or a horse-riding saddle. But, no, it picked flat. https://www.space.com/42202-why-we-need-cosmic-inflation.html
Simply put, if the universe were not ‘ever-so-boringly’ flat (and if the universal constants were not also ‘ever-so-boringly’ constant), but the universe were instead governed by randomness, as atheists presuppose, or governed by some other of the infinitude of ‘platonic topologies’ that were possible, modern science and technology would have never gotten off the ground here on earth.
Scientists Question Nature’s Fundamental Laws – Michael Schirber – 2006 Excerpt: “There is absolutely no reason these constants should be constant,” says astronomer Michael Murphy of the University of Cambridge. “These are famous numbers in physics, but we have no real reason for why they are what they are.”,,, The observed differences are small-roughly a few parts in a million-but the implications are huge (if they hold up): The laws of physics would have to be rewritten, not to mention we might need to make room for six more spatial dimensions than the three that we are used to.”,,, The speed of light, for instance, might be measured one day with a ruler and a clock. If the next day the same measurement gave a different answer, no one could tell if the speed of light changed, the ruler length changed, or the clock ticking changed. http://www.space.com/2613-scientists-question-nature-fundamental-laws.html
Nor, if platonic perfection were not present for the flatness of the universe would we have eventually been able to deduce the ‘platonic perfection’ that is revealed in the ‘higher dimensional’ mathematics that lay behind Relativity and Quantum Mechanics.
The Unreasonable Effectiveness of Mathematics in the Natural Sciences – Eugene Wigner – 1960 Excerpt: We now have, in physics, two theories of great power and interest: the theory of quantum phenomena and the theory of relativity.,,, The two theories operate with different mathematical concepts: the four dimensional Riemann space and the infinite dimensional Hilbert space, http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html
Simply put, no experimental test to date has ever been able to detect any ‘imperfection’ for what the “platonically perfect’ theories of Special Relativity, General Relativity, Quantum-Electrodynamics, and Quantum Mechanics predict.
"Recent experiments have confirmed, to within one part in one hundred million billion (10^17), that the speed of light does not change when an observer is in motion." - Douglas Ell - "Counting To God" - pg. 41 - 2014 Experiment with speeding ions verifies relativistic time dilation to new level of precision - Sept. 19, 2014 Excerpt: A team of researchers,, have conducted an experiment using ions pushed to 40 percent of the speed of light to verify time dilation to a new level of precision.,, the team describes how their experiment was conducted and how it allowed them to validate the time dilation prediction to just a few parts per billion.,,, The experiment allowed for measuring the shift in laser frequencies relative to what the transition frequencies would be for ions that had not been accelerated. By combining the two frequency shifts, uncertainties could be eliminated making it possible to validate time dilation predictions to an order of precision much higher than previous limits,, http://phys.org/news/2014-09-ions-relativistic-dilation-precision.html “On the other hand, I disagree that Darwin’s theory is as `solid as any explanation in science.; Disagree? I regard the claim as preposterous. Quantum electrodynamics is accurate to thirteen or so decimal places; so, too, general relativity. A leaf trembling in the wrong way would suffice to shatter either theory. What can Darwinian theory offer in comparison?” (Berlinski, D., “A Scientific Scandal?: David Berlinski & Critics,” Commentary, July 8, 2003) "When this paper was published (referring to the circa 1970 Hawking, Penrose paper) we could only prove General Relativity's reliability to 1% precision, today we can prove it to 15 places of decimal." Hugh Ross PhD. Astrophysics - quote taken from 8:40 mark of the following video debate Hugh Ross vs Lewis Wolpert - Is there evidence for a Cosmic Creator https://www.youtube.com/watch?v=VLMrDO0_WvQ The Most Precisely Tested Theory in the History of Science - May 5, 2011 Excerpt: So, which of the two (general relativity or QED) is The Most Precisely Tested Theory in the History of Science? It’s a little tough to quantify a title like that, but I think relativity can claim to have tested the smallest effects. Things like the aluminum ion clock experiments showing shifts in the rate of a clock set moving at a few m/s, or raised by a foot, measure relativistic shifts of a few parts in 10^16. That is, if one clock ticks 10,000,000,000,000,000 times, the other ticks 9,999,999,999,999,999 times. That’s an impressively tiny effect, but the measured value is in good agreement with the predictions of relativity. In the end, though, I have to give the nod to QED, because while the absolute effects in relativity may be smaller, the precision of the measurements in QED is more impressive. Experimental tests of relativity measure tiny shifts, but to only a few decimal places. Experimental tests of QED measure small shifts, but to an absurd number of decimal places. The most impressive of these is the “anomalous magnetic moment of the electron,” expressed is terms of a number g whose best measured value is: g/2 = 1.001 159 652 180 73 (28) Depending on how you want to count it, that’s either 11 or 14 digits of precision (the value you would expect without QED is exactly 1, so in some sense, the shift really starts with the first non-zero decimal place), which is just incredible. And QED correctly predicts all those decimal places (at least to within the measurement uncertainty, given by the two digits in parentheses at the end of that). http://scienceblogs.com/principles/2011/05/05/the-most-precisely-tested-theo/ Experimental non-classicality of an indivisible quantum system - Zeilinger 2011 Excerpt: Page 491: "This represents a violation of (Leggett's) inequality (3) by more than 120 standard deviations, demonstrating that no joint probability distribution is capable of describing our results." The violation also excludes any non-contextual hidden-variable model. The result does, however, agree well with quantum mechanical predictions, as we will show now.,,, https://vcq.quantum.at/fileadmin/Publications/Experimental%20non-classicality%20of%20an%20indivisible.pdf
bornagain77

Moreover, contrary to what is commonly believed, Laplace did not really solve the problem of planetary perturbations in the end, (he only solved for for first degree approximations), but Haret showed that orbits are not absolutely stable using third degree approximations. Moreover, I hold that if Newton and Leibniz (and even Laplace) could see our science today they would be very pleased by what modern science has now revealed about the wisdom and power of God in solving the problem of ‘perturbations’:
Of Gaps, Fine-Tuning and Newton’s Solar System - Cornelius Hunter - July 2011 Excerpt: The new results indicate that the solar system could become unstable if diminutive Mercury, the inner most planet, enters into a dance with Jupiter, the fifth planet from the Sun and the largest of all. The resulting upheaval could leave several planets in rubble, including our own. Using Newton’s model of gravity, the chances of such a catastrophe were estimated to be greater than 50/50 over the next 5 billion years. But interestingly, accounting for Albert Einstein’s minor adjustments (according to his theory of relativity), reduces the chances to just 1%. http://darwins-god.blogspot.com/2011/07/of-gaps-fine-tuning-and-newtons-solar.html “You might also think that these disparate bodies are scattered across the solar system without rhyme or reason. But move any piece of the solar system today, or try to add anything more, and the whole construction would be thrown fatally out of kilter. So how exactly did this delicate architecture come to be?” R. Webb – Unknown solar system 1: How was the solar system built? – New Scientist – 2009 Is the Solar System Stable? By Scott Tremaine – 2011 Excerpt: So what are the results? Most of the calculations agree that eight billion years from now, just before the Sun swallows the inner planets and incinerates the outer ones, all of the planets will still be in orbits very similar to their present ones. In this limited sense, the solar system is stable. However, a closer look at the orbit histories reveals that the story is more nuanced. After a few tens of millions of years, calculations using slightly different parameters (e.g., different planetary masses or initial positions within the small ranges allowed by current observations) or different numerical algorithms begin to diverge at an alarming rate. More precisely, the growth of small differences changes from linear to exponential:,,, As an example, shifting your pencil from one side of your desk to the other today could change the gravitational forces on Jupiter enough to shift its position from one side of the Sun to the other a billion years from now. The unpredictability of the solar system over very long times is of course ironic since this was the prototypical system that inspired Laplacian determinism. Fortunately, most of this unpredictability is in the orbital phases of the planets, not the shapes and sizes of their orbits, so the chaotic nature of the solar system does not normally lead to collisions between planets. However, the presence of chaos implies that we can only study the long-term fate of the solar system in a statistical sense, by launching in our computers an armada of solar systems with slightly different parameters at the present time—typically, each planet is shifted by a random amount of about a millimeter—and following their evolution. When this is done, it turns out that in about 1 percent of these systems, Mercury’s orbit becomes sufficiently eccentric so that it collides with Venus before the death of the Sun. Thus, the answer to the question of the stability of the solar system—more precisely, will all the planets survive until the death of the Sun—is neither “yes” nor “no” but “yes, with 99 percent probability.” https://www.ias.edu/about/publications/ias-letter/articles/2011-summer/solar-system-tremaine
Since Albert Einstein’s General Relativity equation reduces the chances to just 1%, and since KF referenced pi in his OP, it is interesting to note that pi is integral to Einstein’s General Relativity equation:
Image- Einstein’s General Relativity equation https://telescoper.files.wordpress.com/2015/11/einstein-equation1.png
Since science has a long history of looking for the ‘idealized situation’ of ‘platonic perfection’, and since KF referenced pi in his OP, it is interesting to note where in this universe ‘platonic perfection’ for spheres is approached rather closely,,,
Sun’s Almost Perfectly Round Shape Baffles Scientists – (Aug. 16, 2012) — Excerpt: The sun is nearly the roundest object ever measured. If scaled to the size of a beach ball, it would be so round that the difference between the widest and narrow diameters would be much less than the width of a human hair.,,, They also found that the solar flattening is remarkably constant over time and too small to agree with that predicted from its surface rotation. http://www.sciencedaily.com/re.....150801.htm Bucky Balls – Andy Gion Excerpt: Buckyballs (C60; Carbon 60) are the roundest and most symmetrical large molecule known to man. Buckministerfullerine continues to astonish with one amazing property after another. C60 is the third major form of pure carbon; graphite and diamond are the other two. Buckyballs were discovered in 1985,,, http://www.3rd1000.com/bucky/bucky.htm Electron’s Nearly Perfect Roundness Stymies The Search For “New Physics” - October 19, 2018 https://uncommondesc.wpengine.com/intelligent-design/electrons-nearly-perfect-roundness-stymies-the-search-for-new-physics/
The delicate balance at which carbon is synthesized in stars is truly a work of art.,,, Years after Sir Fred discovered the stunning precision with which carbon is synthesized in stars he stated this:
“I do not believe that any physicist who examined the evidence could fail to draw the inference that the laws of nuclear physics have been deliberately designed with regard to the consequences they produce within stars.” Sir Fred Hoyle – “The Universe: Past and Present Reflections.” Engineering and Science, November, 1981. pp. 8–12
And ‘platonic perfection’ for a sphere is also approached rather closely in the Cosmic Background Radiation (CBR). ,,, Of the supposed “imperfections” in the sphere of the CBR, the following author comments, “the discovery of small deviations from smoothness (anisotopies) in the cosmic microwave background is welcome, for it provides at least the possibility for the seeds around which structure formed in the later Universe”
The Cosmic Background Radiation Excerpt: These fluctuations are extremely small, representing deviations from the average of only about 1/100,000 of the average temperature of the observed background radiation. The highly isotropic nature of the cosmic background radiation indicates that the early stages of the Universe were almost completely uniform. This raises two problems for (a naturalistic understanding of) the big bang theory. First, when we look at the microwave background coming from widely separated parts of the sky it can be shown that these regions are too separated to have been able to communicate with each other even with signals traveling at light velocity. Thus, how did they know to have almost exactly the same temperature? This general problem is called the horizon problem. Second, the present Universe is homogenous and isotropic, but only on very large scales. For scales the size of superclusters and smaller the luminous matter in the universe is quite lumpy, as illustrated in the following figure. ,,, Thus, the discovery of small deviations from smoothness (anisotopies) in the cosmic microwave background is welcome, for it provides at least the possibility for the seeds around which structure formed in the later Universe. However, as we shall see, we are still far from a quantitative understanding of how this came to be. http://csep10.phys.utk.edu/astr162/lect/cosmology/cbr.html
And indeed, these imperfections in the the sphere of the CMBR, (which ‘provides at least the possibility for the seeds around which structure formed in the later Universe’), ‘surprising’ line up with the earth, and thus overturns the Copernican principle by showing the earth has a ‘privileged position’ in this universe. This fact is touched upon in further detail in the following post:
Thus, contrary to the presumption of atheists, far from the temperature variations in the CMBR being a product of randomness as they presuppose, the temperature variations in the CMBR correspond to the ‘largest scale structures of the observable universe’ and these ‘largest scale structures of the observable universe’ reveal “a surprising rotational coincidence for Earth”. Moreover, the way in which they were able to detect the anomalies in the CMBR, which ‘strangely’ line up with the earth and solar system, is that they ‘smeared’ and/or ‘averaged out’ the tiny temperature variations in the CMBR.,,, (and that ‘average’ corresponds to the earth and solar system) In other words, the “tiny temperature variations” in the CMBR, (from the large scale structures in the universe, to the earth and solar system themselves), reveal teleology, (i.e. a goal directed purpose, a plan), that specifically included the earth from the very beginning of the universe. ,,, The earth, from what our best science can now tell us, is certainly not a random cosmic fluke as atheists presuppose (but was planned from the get go.,,,etc.. etc.. Genesis 1:1-3 In the beginning God created the heavens and the earth. The earth was without form, and void; and darkness was on the face of the deep. And the Spirit of God was hovering over the face of the waters. Then God said, “Let there be light”; and there was light. https://uncommondesc.wpengine.com/intelligent-design/our-solar-system-is-a-lot-rarer-than-it-was-a-quarter-century-ago/#comment-669546
The one exception to this rule of ‘no platonic perfection’ for 3-D Euclidean objects within this universe is the axiomatic ‘primitive object’ in Euclidean geometry of the line.
“When a geometry is described by a set of axioms, the notion of a line is usually left undefined (a so-called primitive object).” https://en.wikipedia.org/wiki/Line_(geometry)
bornagain77

Hazel objects that KF's model is an 'idealized situation' that is 'pure math'. Hazel further objects that "Examples like this one, or even examples where a mathematical model accurately describes actual events in the physical world, do not establish, with “demonstrable warrant”, his philosophical claims about abstract math concepts existing outside and prior to the physical world." Basically Hazel is arguing that the applicability of mathematics to the physical world, no matter how uncanny and accurate it may be, is just a 'happy coincidence' that needs no further explanation. Hazel is hardly the first of the atheistic persuasion to do so. Rosenberg did so in his debate against Dr. Craig.
1. If God did not exist the applicability of mathematics would be a happy coincidence. 2. The applicability of mathematics is not a happy coincidence. 3. Therefore, God exists. - Mathematics and Physics – A Happy Coincidence? – William Lane Craig – video https://www.youtube.com/watch?v=BF25AA4dgGg
And while I agree with Hazel overall sentiment that abstract mathematical objects, being causally inert as they are, do not exist independently, all by their lonesome, 'outside and prior to' the physical world, but are dependent on the Mind of God in order to 'breathe fire into the equations',,,
BRUCE GORDON: Hawking's irrational arguments - October 2010 Excerpt: The physical universe is causally incomplete and therefore neither self-originating nor self-sustaining. The world of space, time, matter and energy is dependent on a reality that transcends space, time, matter and energy. This transcendent reality cannot merely be a Platonic realm of mathematical descriptions, for such things are causally inert abstract entities that do not affect the material world. Neither is it the case that “nothing” is unstable, as Mr. Hawking and others maintain. Absolute nothing cannot have mathematical relationships predicated on it, not even quantum gravitational ones. Rather, the transcendent reality on which our universe depends must be something that can exhibit agency - a mind that can choose among the infinite variety of mathematical descriptions and bring into existence a reality that corresponds to a consistent subset of them. This is what “breathes fire into the equations and makes a universe for them to describe.” Anything else invokes random miracles as an explanatory principle and spells the end of scientific rationality. http://www.washingtontimes.com/news/2010/oct/1/hawking-irrational-arguments/
,,, While I agree with that overall sentiment of Hazel's, I certainly disagree with her overall atheistic sentiment that the uncanny correspondence is just a 'happy coincidence'. Besides Wigner, Einstein himself also rejected the notion that the applicability of mathematics to the physical world is 'just' a 'happy coincidence' but also regarded the uncanny correspondence between math and the physical world to be a 'miracle'.
On the Rational Order of the World: a Letter to Maurice Solovine - Albert Einstein - March 30, 1952 Excerpt: "You find it strange that I consider the comprehensibility of the world (to the extent that we are authorized to speak of such a comprehensibility) as a miracle or as an eternal mystery. Well, a priori, one should expect a chaotic world, which cannot be grasped by the mind in any way .. the kind of order created by Newton's theory of gravitation, for example, is wholly different. Even if a man proposes the axioms of the theory, the success of such a project presupposes a high degree of ordering of the objective world, and this could not be expected a priori. That is the 'miracle' which is constantly reinforced as our knowledge expands. There lies the weakness of positivists and professional atheists who are elated because they feel that they have not only successfully rid the world of gods but “bared the miracles." -Albert Einstein http://inters.org/Einstein-Letter-Solovine
And again, to repeat Wigner's original 'miracle' quotes,,,
The Unreasonable Effectiveness of Mathematics in the Natural Sciences - Eugene Wigner - 1960 Excerpt: ,,certainly it is hard to believe that our reasoning power was brought, by Darwin's process of natural selection, to the perfection which it seems to possess.,,, It is difficult to avoid the impression that a miracle confronts us here, quite comparable in its striking nature to the miracle that the human mind can string a thousand arguments together without getting itself into contradictions, or to the two miracles of the existence of laws of nature and of the human mind's capacity to divine them.,,, The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it and hope that it will remain valid in future research and that it will extend, for better or for worse, to our pleasure, even though perhaps also to our bafflement, to wide branches of learning. http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html
Amazingly, in the original Wigner thread Hazel tried to claim that “I can’t find anything about Wigner attributing the unreasonable effectiveness of math to God.” To which I had to remind her exactly what the definition of a miracle actually is:
mir·a·cle noun a surprising and welcome event that is not explicable by natural or scientific laws and is therefore considered to be the work of a divine agency.
Also in the original Wigner thread I noted that Darwinian evolution, based on materialism as it is, denies the reality of anything beyond the the physical world. This denial extends to the timeless immaterial 'Platonic' world of mathematics.
What Does It Mean to Say That Science & Religion Conflict? – M. Anthony Mills – April 16, 2018 Excerpt: In fact, more problematic for the materialist than the non-existence of persons is the existence of mathematics. Why? Although a committed materialist might be perfectly willing to accept that you do not really exist, he will have a harder time accepting that numbers do not exist. The trouble is that numbers — along with other mathematical entities such as classes, sets, and functions — are indispensable for modern science. And yet — here’s the rub — these “abstract objects” are not material. Thus, one cannot take science as the only sure guide to reality and at the same time discount disbelief in all immaterial realities. https://www.realclearreligion.org/articles/2018/04/16/what_does_it_mean_to_say_that_science_and_religion_conflict.html
And as was further pointed out in that thread, Darwinian materialists, although they deny that anything beyond the material realm exists, need this transcendent world of mathematics in order for their theory to even be considered scientific in the first place. The predicament that Darwinists find themselves in regards to denying the reality of this transcendent, immaterial, world of mathematics, and yet needing validation from this transcendent, immaterial, world of mathematics in order to be considered scientific, should be the very definition of a scientifically self-refuting theory. But it is hardly surprising that Darwinists ignore the fact that their materialistic theory, which denies the reality of the immaterial realm altogether, is dependent on this immaterial realm of mathematics in order to be considered scientific in the first place, Darwinists have a long history of ignoring the fact that their theory has been shown to be mathematically impossible by many different methods.
Darwinian Evolution vs Mathematics - video https://www.youtube.com/watch?v=q3gyx70BHvA
Which is again proof that, when it comes to Darwinian evolution, we are basically dealing with a unfalsifiable pseudo-scientific religion for atheists, rather than dealing with any mathematically well defined and rigorous theory of science that can be 'potentially' falsified by empirical testing:
Darwin’s Theory vs Falsification – video https://www.youtube.com/watch?v=8rzw0JkuKuQ “Before you can ask 'Is Darwinian theory correct or not?', You have to ask the preliminary question 'Is it clear enough so that it could be correct?'. That's a very different question. One of my prevailing doctrines about Darwinian theory is 'Man, that thing is just a mess. It's like looking into a room full of smoke.' Nothing in the theory is precisely, clearly, carefully defined or delineated. It lacks all of the rigor one expects from mathematical physics, and mathematical physics lacks all the rigor one expects from mathematics. So we're talking about a gradual descent down the level of intelligibility until we reach evolutionary biology.” - David Berlinski
Hazel went further than just saying that KF's model was an 'idealized situation' that neglected friction, (the second law and such as that), but Hazel also further claimed that even if 'a mathematical model accurately describes actual events in the physical world', that still would 'not establish, with “demonstrable warrant”, his (KF's) philosophical claims about abstract math concepts existing outside and prior to the physical world." Hazel’s use of the term 'idealized situation' gives her hand away. If she rejects KF’s model because it is an 'idealized situation' that only exists in the mind of man and not in the physical world, then she should accept the fact that when a mathematical model is found to ‘accurately describe’ that “idealized situation” of math within the physical world, with no discrepancies, then by all rights she should accept that that “idealized situation” of math and the physical world is the product of an ‘Idea’ that originates in the Mind of God, not by some unfathomable physical process. Hazel, inadvertently and unavoidably, with her use of the term 'idealized situation' revealed her philosophical bias against God when that 'idealized situation' of math is actually reached in the physical world. Moreover, science has a long history of looking for 'platonic perfection' in the physical world and assuming the Mind of God to be behind that ‘platonic perfection’.
“Mathematics is the language with which God has written the universe.” Galileo Galilei “Geometry is unique and eternal, a reflection from the mind of God. That mankind shares in it is because man is an image of God.” – Johannes Kepler
Copernicus, (who was heavily influenced by Platonic thinking), imagined (incorrectly) that the planets move in perfect circles (rather than ellipses). Later, Newton, for allowing God could adjust the orbits of the planets, was chastised by Leibniz, (and Laplace) for having a “very narrow ideas about the wisdom and the power of God.”.. i.e. For having a narrow view of the perfection of God. In fact, Laplace, contrary to atheistic folklore, cited with approval Leibniz’s criticism of Newton’s invocation of divine intervention to restore order to the Solar System: “This is to have very narrow ideas about the wisdom and the power of God.”, to them, it would count as evidence against intelligent design if God had to intervene to prevent the solar system from collapsing. So intelligent design could just as easily be a motivation to prove the stability of the solar system.
“Leibniz, in his controversy with Newton on the discovery of infinitesimal calculus, sharply criticized the theory of Divine intervention as a corrective of the disturbances of the solar system. “To suppose anything of the kind”, he said, “is to exhibit very narrow ideas of the wisdom and power of God’.” – Pierre-Simon Laplace https://books.google.com/books?id=oLtHAAAAIAAJ&pg=PA73&lpg=PA73
Even according to wikipedia (hardly an ID friendly website), Laplace paraphrase is shown to be based on folklore not on fact,
In 1884, however, the astronomer Hervé Faye[76][77] affirmed that this account of Laplace's exchange with Napoleon presented a "strangely transformed" (étrangement transformée) or garbled version of what had actually happened. It was not God that Laplace had treated as a hypothesis, but merely his intervention at a determinate point: https://en.wikipedia.org/wiki/Pierre-Simon_Laplace#Religious_opinions
bornagain77

ET (attn H): First, the warrant laid out in the other thread, which pivots on the inescapably true principle of distinct identity as a core premise of being and on the linked premise that if two things W1 and W2 are indistinguishable they are merely labels for the same entity W, thence what the implications for a world-distinctive A are, not assumptions or assertions about minds -- this is an argument to necessary abstract entities embedded in the fabric of any distinct world . . . thus that certain quantities and structures are substantially present once any world is:
1: Consider reality, and within it some distinct entity, say a bright red ball on a table, B. Thus the rest of reality is the complement to B, ~B. Reality, R = {B|~B} 2: Immediately, B is itself (distinctly identifiable i/l/o its core, distinguishing characteristics), this is the fundamental law of thought, Law of Identity, which sets up the dichotomy and its corollaries. 3: Clearly, no x in R can be B AND ~B. Law of non-contradiction, a corollary. 4: Likewise, any x in R must be in B or in ~B, not between them or separate from them: B X-OR ~B, law of the excluded middle. The second corollary. 5: Now, ponder a possible world, W, a sufficiently complete description of a possible [coherent!] state of affairs in reality,i.e. in this or any other world that could be or is. 6: So far, we have set up a framework for discussion, including pointing out the key first principles of right reason that we must use so soon as we type out a message using distinct characters, etc. These are not provable, they are inevitable, inescapable and thus have a right to be presumed first truths of right reason. 7: Now, W, holds distinct identity, it is a particular possible world, different from all others. That is, if claimed entities W1 and W2 are not discernibly different in any respect, they are just different labels for the same thing W. 8: Notice, all along we are trafficking in statements that imply or assert that certain things are so or are not so, i.e. propositions and that relationship of accurate description of reality that we term truth. 9: All of these are not merely concrete particulars or mere labels, they are abstracta which are inevitable in reasoning. Indeed, the relationship of intentionality implicit in attaching a name is an abstractum, too. 10: Now, W is one of infinitely many possible states of affairs, and shares many attributes in common with others. So, we mark the in-common [genus] and the distinct [differentia]. 11: So, we freely identify some unique aspect of W, A. W, then is: W = {A|~A}. 12: But already, we see rationally discernible abstract entities, principles and facts or relationship, quantity and structure; i.e. the SUBSTANCE of Mathematics. Namely, 13: first, that which is in W but external to A and ~A is empty, as is the partition: nullity. 14: Likewise, A is a distinct unit, as is ~A [which last is obviously a complex unity]. This gives us unity and duality. 15: So, simply on W being a distinct possible world, we must have in it nullity, unity and duality. These are abstract structural and quantitative properties embedded in the framework for W. 16: This is, strictly, already enough for the claim that there is an abstract substance of mathematical character that is necessarily embedded in any possible world, which is itself an abstract entity, being a collection of propositions. In at least one case such are actualised, i.e. it is possible to have an accurate summary of our world. 17: However, much more is necessarily present, once we see the force of the von Neumann succession of ordinals (which substantiates Peano’s succession), actually presenting the natural counting numbers starting from the set that collects nothing, which is itself an undeniable abstract entity: {} –> 0 {0} –> 1 {0,1) –> 2 {0,1,2} –> 3 . . . {0,1,2,3 . . . } –> w [first transfinite ordinal] etc, without limit 18: We here have N. Define for some n in N, that -n is such that n + (-n) = 0, and we equally necessarily have Z. Again, rooted in the distinct identity of a world, we are studying, exploring, discovering, warranting (as opposed to proving), not creating through our culturally influenced symbolism and discussion. 19: Similarly, identify the ratio n:m, and we attain the rationals, Q. 20: Use power series expansions to capture whole part + endless sum of reducing fractions converging on any given value such as pi or e or phi etc, and we have the reals, R, thus also the continuum. Where, from Z on, we have has entities with magnitude and direction, vectors. 21: Now, propose an operation i*, rotation pivoting on 0 through a right angle. This gives us i*R, an orthogonal axis with continuum, and where for any r in R+, i*r is on the new [y] axis. 22: Now too, go i*i*r, and we find -r. That is we have that i = sqrt(-1), which here has a natural sense as a vector rotation. Any coordinate in the xy plane as described is now seen as a position vector relative to the origin. 23: We have abstract planar space, thus room for algebraic and geometrical contemplation of abstract, mathematically perfect figures. For instance consider the circle r^2 = x^2 + y^2, centred on o. 24: In its upper half let us ponder a triangle standing at -r [A] and r [B] with third vertex at C on the upper arc. This is a right angle triangle with all associated spatial properties, starting with angle sum triangle and Pythagorean relationships, trig identities etc. Between these two figures and extensions, the world of planar figures opens up. 25: Extend rotations to ijk unit vectors and we are at 3-d abstract “flat” space. All of this, tracing to distinct identity. 26: We may bring in Quaternions and Octonions, the latter now being explored as a context for particle physics. 27: The Wigner Math-Physics gap is bridged, at world-root level. 28: Similarly, we have established a large body of intelligible, rational entities and principles of structure and quantity implicit in distinct identity. Such are the substance we discover by exploration (which is culturally influenced) rather than invent. 29: Where it is an obvious characteristic of invention, that it is temporally bound past-wards, Until some time t, entity e did not exist. Then, after t, having been created, it now exists. 30: The above abstracta are implicit in the distinct identity of a world and so have existed so long as reality has. That is, without past bound. (It can readily be shown that if a world now is, some reality always was.)
To date, no-one has provided a counter-demonstration. Where, to deny LOI and its immediate corollaries is intellectually immediately absurd. Next, the above case studies demonstrate facts of discovery that in this world where Newtonian dynamics have a realm of validity, we can see that in fact we discover many embedded abstract quantities and structures. The case on number of collisions showing successive digits of pi turns on influences of energy and momentum conservation which are observable and mathematically demonstrable on pondering cumulative effects of forces [pushes or pulls -- already, vectors] across space and time. In turn, that brings to bear infinitesimals and the key operations of calculus, rates and accumulations. Energy is abstract as is momentum, force by contrast is tangible. Further, its phase space shows how geometric abstract considerations on conservation of kinetic energy and momentum (already abstracta) lead to a geometric pattern that produces the result. Going to projectiles we see vector components and different force effects thus dynamics of projectile motion. The case of the capilliarity between wedged glass blocks producing a hyperbola shows calculus again and patently direct embedding of quantities and structures. The semi-circle and string thought exercise would show embedding of abstract geometrical structures and patterns in space. The Mobius strip, spectacularly so. These things are manifesting such properties in contexts that are not merely conceptual, they are concretely physical. And we could continue. KF kairosfocus

hazel:
But kf claims that pure math concepts exist outside of the individual minds which understand them, …
What? ID says the Intelligent Design was from a Mind. And if math was used to design the physical world then it is obvious that the Designing Mind understood them.
...and that the pure math existed before (“antecedent to” is his phrase) the existence of the physical world.
That Intelligent Designer, again.
Examples like this one, or even examples where a mathematical model accurately describes actual events in the physical world, do not establish, with “demonstrable warrant”, his philosophical claims about abstract math concepts existing outside and prior to the physical world.
Except it is not a philosophical claim. ET

F/N2: My objective here is to hammer home through accessible and undeniably relevant case studies just how pervasively the Wigner Math-Physics gap is bridged. Understanding deep in our bones through seeing a pervasive pattern is necessary to break the spells of Kantian ugly gaps and associated subjectivism, relativism and nominalism. That's what will have to be done to rescue Math, Physics, logic and understanding of being from what we have been seeing for weeks. We have been bewitched. KF PS: I added a Mobius strip cutting exercise to the OP -- simple case. kairosfocus

F/N: I should speak to potential energy, that which is locked into position (in a force field) or state -- chemical, nuclear -- etc. In this case, consider an old fashioned cannon, elevated at an angle. First, in vacuo -- a simple ideal case. Fire a ball, and away it goes, projected with initial velocity [muzzle velocity], with mass, at an angle. A simple analysis will see its velocity breaks into vertical and horizontal components. The latter, leads to steady horizontal speed. The former undergoes uniform gravitationally induced acceleration downwards, leading to climbing to a peak and descending symmetrically again. This shows how the initial KE of vertical motion is converted gradually -- at the rate that follows from PE = m*g*h -- into positional energy in the gravity field and then returns to KE under conservation of energy. Rich onward aspects lurk, including how a gravity potential well marks a warping of the spacetime fabric due to mass. The result of the two is that the projectile follows a parabola, and in many cases where air resistance is not material, that can be seen pretty directly. A parabola of course being one of the five conic sections. (I used to look at such using conically tapered drinking glasses: circles, ellipses, parabolas, hyperbolas. Straight lines are trivial. Also note, "orbital" paths for objects in a gravity well follow conic sections (unless perturbed, which then leads on to butterfly effects and chaos!) Coming back, we can consider air resistance (an example of taking an ideal model and bringing in further factors to more accurately address complexities of cases) and how it affects the components, leading to complex ballistics models, which bleed over into modelling flight (often, by way of rockets and guided missiles these days). And of course, we see more and more structural and quantitative abstracta embedded in physical reality. Going back to PE, capillarity provides a striking case study which I originally encountered by accident. For some reason I now forget, I was using two optical glass blocks sitting in water tinted with ink, to illustrate the effect. Somehow, I set the blocks in a narrow, v-shaped wedge. Instantly, the liquid that had been pulled up above the surface ran up into a sharply defined, instantly recognised hyperbola. Why? I went to the board and did a live modelling exercise. We know, liquid molecules wet glass showing adhesion, and they stick together [balanced by intermolecular repulsion that sharply rises as they are compressed and molecular electron clouds begin to overlap]. So, consider that the surface adhesion at the meniscus is lifting an entrained column of liquid through h consistent with force balance, F_adh = - mgh. So, now, consider an increment dx along the blocks of width z is lifted to h, where dx * z*h is the lifted volume, of mass density * lifted volume. At this level, in effect this is a tiny rectangular prism. It soon drops out that h is inversely proportional to x, length along the face of the block from the apex of the V. A striking case that brings together infinitesimals, structural and quantitative constraints and more, yielding to close approximation a well recognised mathematical result. (I soon realised that if done carefully, the curve would remain on separation and could be transferred to a paper.) I of course then routinely used this case in further classes. Again, we see how anstracta of structure and quantity are deeply embedded in the fabric of the world. KF PS: I recall, too, exercises of gluing together a Mobius strip and cutting around the loop then cutting again: double length strip then two interlocked circles. (See vid here, with bonus on cutting at the 1/3 width point: https://www.youtube.com/watch?v=XlQOipIVFPk and the two-cut discussion here: https://www.wikihow.com/Explore-a-Mobius-Strip then that which is here: http://www.exo.net/~pauld/activities/mobius/mobiusdissection.html see actual video here https://www.youtube.com/watch?v=f-19NLKxNUc ) Likewise, that cutting out a circle then folding over a sector or cutting it out will then lead to forming a right circular cone. An astonishing spatial transformation almost as impressive as the strip, if you think about it. I have already talked about doing a string and half-circle exercise -- pinning threads to the ends of the diameter and along the arc that brings out circle theorem and pythagorean spatial properties. Maybe, I should add, build the squares on the sides and see how the theorem works. Toss in the Euler identity 0 = 1 + e^i*pi for good measure. Space inextricably embeds in itself deep abstract structures and quantities. kairosfocus

H, we have here a case study on how an abstract, dual space that brings out the significance of major conservation laws is intimately involved in the framework of behaviour we see in the time-space domain; the embedding of key domains of structure and quantity in the logic of being in any possible world having already been demonstrated. Where, notice, Geometry in the abstract space is directly relevant to physical world behaviour -- the breakout that allows a count of collisions depends on the double-angle circle theorem exhausts the circumference of a circle. Where, too, such domains in an auxiliary space that demark criteria for crucial behaviour changes are pivotal in other similar analyses. For material example, in the Laplace domain, poles drifting to the right half of the space imply instabilities, and as that threshold is approached, we see ringing behaviour etc. Which is related to the issue of being outside the unit circle in the Z-transform domain. This case study also continues the exploration of how abstract, logic-model possible worlds draw out entities, relationships, structures and quantities which then provide bridging archetypes for the physical world -- hence ways in which we can better understand through case studies how the Wigner Math-Physics gap is bridged. All, in a context of exploring logic and first principles of thought of interest to design theory and wider thinking on serious matters; thought which would not normally be controversial but for the sort of ideologies on the loose in our day. In that explicit context of logic and first principles, the OP introduces a key analytical tool, phase or state or configuration space, which is of great value for itself and which is an extension of how logic -- rational principles -- of structure and quantity are key to the reasoning process we undertake in addressing scientific and other important matters. It specifically serves as a case study that sets the context in which we can see how energy and mass conservation laws lie implicit in the logic of force-based interaction of bodies acting in space and time -- a big result in its own right, and one that in my view should be better brought out in early exposure to physics. This example of a dual, abstract domain and its relevance is also significant as opening the way for consideration of other cases of state/ phase/ configuration spaces and similar uses of abstract domains such as Fourier, Laplace and Z transforms. KF PS: The case study also puts on the table two out of three crucial conservation laws and how they arise: momentum, energy and angular momentum (an extension of conservation of momentum through the analogy of translational and rotational motion). This in turn highlights the physical significance of an abstract, structurally embedded quantity or three. That is already an embedded abstraction -- conservation laws -- that mark major cross-cutting and unifying/bridging themes in Physics. It also puts on the table the significance of three linked abstracta: momentum, angular momentum and energy. Where, too, we see the embedding of a core calculus concept (and fundamental theorem), as momentum is the cumulative effect of force is time, and kinetic energy is the cumulative effect of force in space -- rates and accumulations being key abstracta that thanks to hyperreals and nonstandard analysis, bring back infinitesimals. Angular momentum, per the analogy, is the cumulative effect of torque in time. Where, too inertial quantities play a regulatory role on rates of accumulation. This points to the interesting questions as to what mass, moment of inertia, momentum and energy are. Let Wikipedia speak as a witness testifying against known ideological interest:
In physics, energy is the quantitative property that must be transferred to an object in order to perform work on, or to heat, the object.[note 1] Energy is a conserved quantity; the law of conservation of energy states that energy can be converted in form, but not created or destroyed. The SI unit of energy is the joule, which is the energy transferred to an object by the work of moving it a distance of 1 metre against a force of 1 [N]ewton. Common forms of energy include the kinetic energy of a moving object, the potential energy stored by an object's position in a force field (gravitational, electric or magnetic), the elastic energy stored by stretching solid objects, the chemical energy released when a fuel burns, the radiant energy carried by light, and the thermal energy due to an object's temperature. Mass and energy are closely related. Due to mass–energy equivalence, any object that has mass when stationary (called rest mass) also has an equivalent amount of energy whose form is called rest energy, and any additional energy (of any form) acquired by the object above that rest energy will increase the object's total mass just as it increases its total energy. For example, after heating an object, its increase in energy could be measured as a small increase in mass, with a sensitive enough scale.
Notice, how the operational definition on the unit of energy gives a big clue on its abstract nature. PPS: Notice, now that our eyes are sensitised, how Wiki similarly speaks about momentum:
In Newtonian mechanics, linear momentum, translational momentum, or simply momentum (pl. momenta) is the product of the mass and velocity of an object. [--> actually, this is back-ways, Newton's laws are laws of momentum, "motion" being an older terminology, momentum is the quantification of motion and force is its time rate of change .. the more general, calculus form of the second law, F = dP/dt] It is a vector quantity, possessing a magnitude and a direction in three-dimensional space. If m is an object's mass and v is the velocity (also a vector), then the momentum is p = m v , In SI units, it is measured in kilogram meters per second (kg?m/s). Newton's second law of motion states that a body's rate of change in momentum is equal to the net force acting on it. Momentum depends on the frame of reference [--> a huge topic, one of the core postulates in Relativity being how in an inertial frame of reference the laws of physics take their simplest form], but in any inertial frame it is a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) [--> Relativity builds on classical physics in these aspects] and, in a modified form, in electrodynamics, quantum mechanics, quantum field theory, and general relativity. It is an expression of one of the fundamental symmetries of space and time: translational symmetry. Advanced formulations of classical mechanics, Lagrangian and Hamiltonian mechanics, allow one to choose coordinate systems that incorporate symmetries and constraints. In these systems the conserved quantity is generalized momentum, and in general this is different from the kinetic momentum defined above. The concept of generalized momentum is carried over into quantum mechanics, where it becomes an operator on a wave function. The momentum and position operators are related by the Heisenberg uncertainty principle.
In this context, the intimate fusing of abstracta of structure and quantity and concrete manifestations in space and time is patent. kairosfocus

Ed, it's a model of an idealized situation based on formulas that are known for the movement and energy of objects. It is all pure math. What it doesn't do is add to kf's arguments. No one has disputed that math can, to varying degrees (sometimes to remarkable degrees), provide accurate models of things that actually happen in the physical world (although I think this particular situation would be hard to actually set up.) That was the whole point of Wigner's essay on the Unreasonable Effectiveness of math, which I don't think anyone has disputed. But kf claims that pure math concepts exist outside of the individual minds which understand them, and use them, and that the pure math existed before ("antecedent to" is his phrase) the existence of the physical world. Examples like this one, or even examples where a mathematical model accurately describes actual events in the physical world, do not establish, with "demonstrable warrant", his philosophical claims about abstract math concepts existing outside and prior to the physical world. hazel

It’s way beyond me. But, possibly, that is the point. Ed George

Actually, after watching further, I see that this is all pure math, using a theoretical model. Still neat, though. hazel

I like applied math. :-) hazel

F/N: Maybe I should add a note on kinetic energy i/l/o kinematics and some basic dynamics of force and work. 1: It is easy to see from uniformly accelerated motion: v^2 = u^2 + 2*a*x, 2: So, rearranging: v^2 - u^2 = 2*a*x, 1/2[v^2 - u^2] = a*x, 3: Where F = m*a (where m is constant) and increment of work, dW = F*dx, so too: 1/2*m*[v^2 - u^2] = m*a*x = F*x = W --> Work done by F applied to a body is linked to change in a velocity-square term, so set u = 0: 1/2*m*v^2 = m*a*x = F*x = W --> 1/2*m*v^2 or kinetic energy, is the net work done to give a body of mass m its velocity v, starting from rest and it is manifest also in the forced motion through relevant distance moved, x. This gives some background to the OP. It also helps us see why kinetic energy will be conserved in the idealised case, KE change comes from forces changing the speed of massive bodies. (BTW, this can be extended to rotational motion.) KF PS: Momentum conservation can be similarly analysed, given that empirically bodies interact in pairs, exerting equal magnitude, oppositely directed forces, where too momentum is in effect cumulative effect of force acting across time. So momentum change in body A of an interacting pair will be equal size but oppositely directed to that of body B. In the cases above, the rigid wall has effectively infinite mass and all momentum change is in the body that hits it. The two moving bodies interact in ways dependent on relative masses and velocities. All of this then has its dual in the phase space view. kairosfocus

Things like this make me look forward even more keenly to being able to question the designer. ScuzzaMan

Logic & First Principles 8: Bridging the Wigner MATH-PHYSICS GAP (with help from phase/ configuration/ state space) kairosfocus

You must be logged in to post a comment.

Leave a Reply