UD commenter Joe notes:
Alan [Fox] amuses by not understanding the definition of “default”. He thinks the design inference is the default even though it is reached via research, observations, knowledge and experiences.
To put this ill-founded but longstanding objection to the design inference — it is tantamount to an accusation of question-begging — to bed permanently, I note:
____________
>> . . . a year after Dr Liddle was repeatedly and specifically corrected that the inference to design is after rejecting not one but TWO defaults, that is still being raised as an objection over at TSZ.
That speaks volumes.
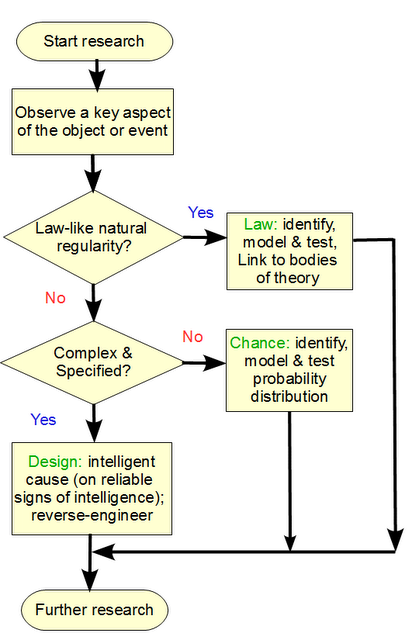
Let’s outline again, for those unable to understand a classic flowchart [even UML preserves a version of this . . .).
{Flowchart of the explanatory filter:
1: Step one, we examine an aspect of an object, phenomenon or process (in science we examine relevant aspects, it did not matter what colour they painted the pendulum bob in assessing its oscillations).
2: Observe enough to see whether we have low or high contingency, i.e. high variability on similar initial conditions.
3: Lawlike regularities lead to inference of mechanical necessity expressible in deterministic laws, like Kepler’s laws of planetary motion, or the law of the simple pendulum with small swings. Or, the observation that dropped heavy objects reliably fall under g = 9.8 N/kg near earth’s surface.
4: If an aspect shows high contingency, this is not reasonably explicable on such a law.
5: Thus, we have to look at the two known sources of high contingency, chance and design. For instance, a dropped die that tumbles and settles can be fair and showing a flat distribution across {1, 2, . . . 6} or it can be artfully loaded. (This example has been cited over and over for years, that it has not sunk in yet is utterly telling on closed mindedness.)
6: The presumed default on high contingency, is chance, showing itself in some typical stochastic distribution, as is say typical of the experimental scatter studied under the theory of errors in science. Dice show a flat distribution if they are fair. Wind speed often follows a Weibull distribution, and so forth.
7: Sampling theory tells us that when we observe such a distribution, we tend to reflect the bulk of the population, and that rare, special zones are unlikely to come up in a sample that is too small. This is the root of Fisherian hypothesis testing commonly used in statistical studies. (As in far tails are special rare zones so if you keep on hitting that zone, you are most likely NOT under a chance based sample. Loaded dice being a typical case in point: as you multiply the number of dice, the distribution tends to have a sharp peak in the middle and for instance, you are very unlikely to get 1,1,1, .. or all sixes etc. The flipped coin as a two sided die, is a classic studied under statistical mechanics.)
8: So, once we have a complex enough case that deeply isolates special zones, we are maximally unlikely to see such by chance. But, the likelihood of seeing such under loading or similar manipulation is a different proposition altogether.
9: WLOG, we may consider a long covered tray of 504 coins in a string with a scanner that reports the state when a button is pushed:
)) — || Tray of coins Black Box || –> 504 bit string
10: Under the chance hyp, with all but certainty, on the gamut of the solar system, we would find the coins with near 50:50 distribution H/T, in no particular order.
11: That is an all but certain expectation on the gamut of the solar system.
12: But if instead we found the first 72 ASCII characters of this post in the 504 bits, we would have strong reason to suspect IDOW as the best explanation. There is no good reason otherwise to see the highly contingent outcome in so isolated a functional state.
13: Thus, having rejected the two defaults, coins are highly contingent and chance is maximally unlikely per the relevant distribution to provide such an outcome with FSCO/I, we infer to design.
14: In short, the logic involved is not so difficult or dubious, it is glorified common sense, backed up by billions of examples that ground an inductive generalisation, and by the needle in the haystack analysis that shows why it is eminently reasonable.
15: What needs to be explained is not why inference to design is reasonable, on seeing FSCO/I. Instead, it is why this is so controversial, given the strength of the case.
16: The answer to that is plain: it cuts across a dominant ideology in our day, evolutionary materialism, which likes to dress itself up in the lab coat and to fly the flag of science.
That, it seems, is the real problem . . . >>
____________
Let’s see if this is enough to settle the matter, and if not, why not. END