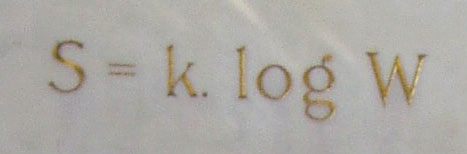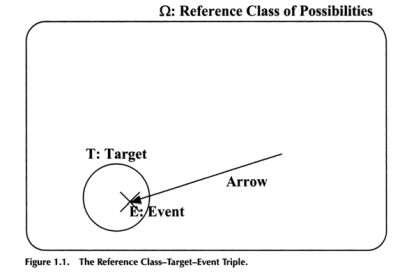
In his well-known work, No Free Lunch, p. 11, ID Researcher William A Dembski has illustrated the search challenge concept in terms of an arrow hitting a target amidst a reference class of possibilities. In so doing, he reaches back to the statistical mechanical and mathematical concept of a phase space “cut down” to address configurations only (leaving out momentum), aka state space. He then goes on to speak in terms of probabilities, observing:
>>. . . in determining whether an event is sufficiently improbable or complex to implicate design, the relevant probability is not that of the event [= E] itself. In the archery example, that probability corresponds to the size of the arrowhead point in relation to the size of the wall and will be minuscule regardless of whether a target [= T] is painted on the wall. Rather the relevant probability is that of hitting the target . . . [corresponding] to the size of the target in relation to the wall and can take any value between zero and one . . . The smaller the target the harder it is to hit it by chance and thus apart from design. The crucial probability then is the probability of the target with respect to the reference class of possible events [= Omega, Ω . . . traditionally used in statistical mechanics]. [NFL, p. 11.]>>
We may now freely correlate this with the AI concept of state-space search, as was recently pointed out in the Answering DiEb UD discussion thread:
KF, 30: >>Note this from Wiki on searches of a state space:
State space search is a process used in the field of computer science, including artificial intelligence (AI), in which successive configurations or states of an instance are considered, with the intention of finding a goal state with a desired property.
Problems are often modelled as a state space, a set of states that a problem can be in. The set of states forms a graph where two states are connected if there is an operation that can be performed to transform the first state into the second.
State space search often differs from traditional computer science search methods because the state space is implicit: the typical state space graph is much too large to generate and store in memory. Instead, nodes are generated as they are explored, and typically discarded thereafter. A solution to a combinatorial search instance may consist of the goal state itself, or of a path from some initial state to the goal state.
Representation
Examples of State-space search algorithms
Uninformed Search
According to Poole and Mackworth, the following are uninformed state-space search methods, meaning that they do not know information about the goal’s location.[1]
Depth-first search
Breadth-first search
Lowest-cost-first searchInformed Search
Some algorithms take into account information about the goal node’s location in the form of a heuristic function[2]. Poole and Mackworth cite the following examples as informed search algorithms:
Heuristic depth-first search
Greedy best-first search
A* searchMuy interesante, no? . . . . Cf my remarks above [which provide a definition of search tied to the state/configuration space concept]:
Several times, you [DiEb] have raised the issue of search [ –> as in, in recent exchanges at UD]. I have pointed out that at base, it is tantamount to sampling from a configuration space.
[As, algebraic representation is commonly desired (and is often deemed superior to illustration or verbal description), a traditional representation of such a space is to symbolise it as Omega, here we can use w. Search then is obviously — and the obviousness is a material point here — tantamount to taking a subset of cases k in w by whatever relevant means, blind or intelligent. The search challenge then is to find some relevant zone z in w such that a performance based on configuration rises above a floor deemed non-functional: find/happen upon some z_i in w such that p(z) GT/eq f_min. Zones z are islands of function in the configuration space, w.]>>
The correlations are patent.
Now, let us adjust. First, the relevant reference class of possibilities is the state or configuration space, Ω [which for combox convenience I and others often represent as w or W]. Here, see Boltzmann’s tomb, recording the key contribution that tragic figure wished to forever be remembered for:
And yes, entropy S is directly connected. (So, too, in the informational sense.)
Next, consider the case where there may be many potential targets, dotted about a — still abstract — space of possibilities and where many searches are conducted in parallel — think of Shakespeare’s King Henry V, with English and Welsh longbow-men at Agincourt facing the French Chivalry [= heavy armoured cavalry] coming at them. Estimates have suggested longbow-men mass-volleys of 40,000 shafts per minute and of the cloud of arrows briefly and brutally shading out the sun. Obviously, this improves the odds of hitting some one or more targets [especially the poor innocent horses], as the outcome of that battle notoriously testifies:
These concrete [though, pardon, awful] real-world cases can help us to now understand the relevant kinds of “search” that ID is addressing.
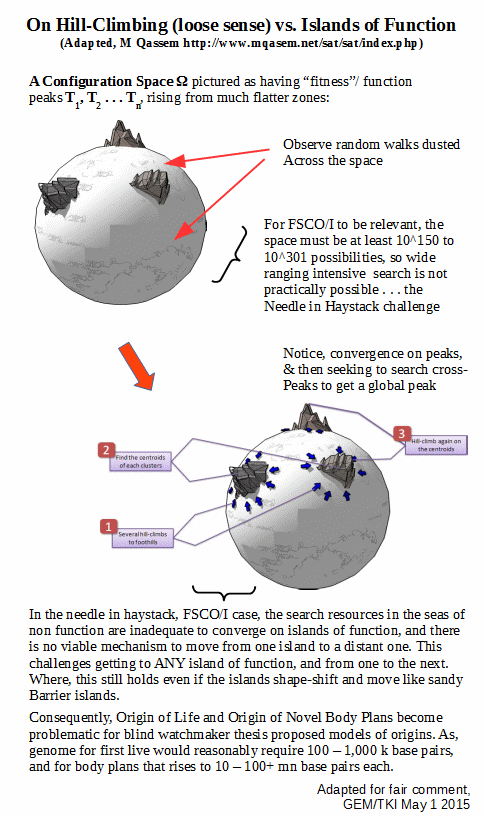
Obviously, a search pattern, whether by one observer or by many in parallel, samples from the space of possibilities, and each individual “shot” can hit or miss the targets, while there is a cost of time and resources for every shot. But now, we first ponder, what happens when targets are isolated and scattered across a vast space of possibilities? Where, also, resources are very limited so in aggregate they will be exhausted long before other than an all-but-zero fraction of the space is sampled? And, what happens if the bowman is blind-folded and deaf so he cannot sense where a target is likely to be? And what if we now revert to purposeless “bow-men” scattering their “shots” at random and/or based on some mechanical necessity not correlated to where targets are?
That is, we are now looking at needle-in-the-haystack, blind search:
In that light, let us now look briefly at a later discussion by Dembski in which he implies that kind of blind bow-men scattershot search. Though, I must request a look with fresh eyes, not the mind full of objections and real or imagined peculiarities and personalities. Notice, how closely Dembski’s conceptions mirror what we have seen above, underscoring the relevance of the description of what search is as relevant to ID:
KF, 22 : >>William A. Dembski and Robert J. Marks II, “The Search for a Search: Measuring the Information Cost of Higher Level Search,” Journal of Advanced Computational Intelligence and Intelligent Informatics, Vol.14, No.5, 2010, pp. 475-486.
Abstract
Needle-in-the-haystack [search] problems look for small targets in large spaces. In such cases, blind search stands no hope of success. Conservation of information dictates any search technique [–> as in not specifically correlated to the structure of the space, i.e. a map of the targets] will work, on average, as well as blind search. Success requires an assisted [intelligently directed, well-informed] search. But whence the assistance required for a search to be successful? To pose the question this way suggests that successful searches do not emerge spontaneously but need themselves to be discovered via a search. The question then naturally arises whether such a higher-level “search for a search” is any easier than the original search.
[–> where once search is taken as implying sample, searches take subsets so the set of possible searches is tantamount to the power set of the original set. For a set of cardinality n, the power set has cardinality 2^n.]
We prove two results: (1) The Horizontal No Free Lunch Theorem, which shows that average relative performance of searches never exceeds unassisted or blind searches, and (2) The Vertical No Free Lunch Theorem, which shows that the difficulty of searching for a successful search increases exponentially with respect to the minimum allowable active information being sought.
1. Introduction
Conservation of information theorems [1–3], especially the No Free Lunch Theorems (NFLT’s) [4–8], show that without prior information about a search environment or the target sought, one search strategy is, on average, as
good as any other [9]. This is the result of the Horizontal NFLT presented in Section 3.2.A search’s difficulty can be measured by its endoge-nous information [1, 10–14] defined as
I_w = – log_2 p …………. (1)
where p is the probability of a success from a random query [1]. When there is knowledge about the target lo-cation or search space structure, the degree to which the search is improved is determined by the resulting active information[1, 10–14]. Even moderately sized searches are virtually certain to fail in the absence of knowledge about the target location or the search space structure. Knowledge concerning membership of the search prob-lem in a structured class [15], for example, can constitute search space structure information [16].
Endogenous and active information together allow for a precise characterization of the conservation of
informa-tion. The average active information, or active entropy,of an unassisted search is zero when no assumption is made concerning the search target. If any assumption is made concerning the target, the active entropy becomes negative. This is the Horizontal NFLT presented in Sec-tion 3.2. It states that an arbitrary search space structure will, on average, result in a worse search than assuming nothing and simply performing an unassisted search . . . >>
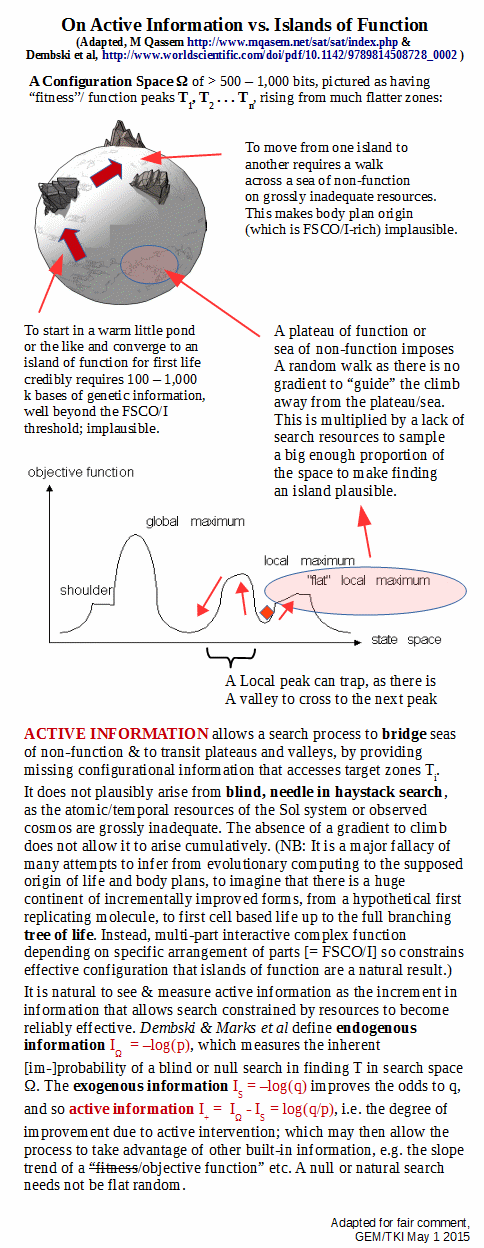
Here, searches can come from a configuration space of possibilities blindly by chance and/or by some mechanism which in general is not correlated to the target-map of the space of possibilities. Once the ratio of space to target approaches the needle in haystack challenge level, blind searches are not a plausible means of getting to one or more targets. In that context the gap between blind search and observed hitting of targets is best explained on direction through so-called active information. That may be externally provided or may arise from an implicit mapping by hill climbing on a performance that rises above a floor of non-function, once the space has a sufficiently smooth slope that such will not fall into the pitfalls for hill-climbing.
Function based on complex, coherent, information-rich organisation — functionally specific, complex organisation and/or information [FSCO/I] is now present. As an illustration:
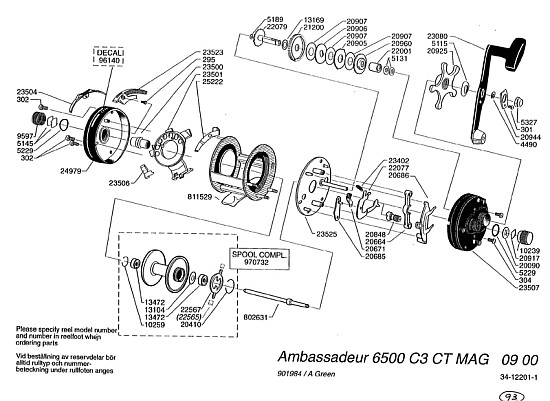
Just for fun, let me add [Feb 3] an illustration of gearing found in life forms:
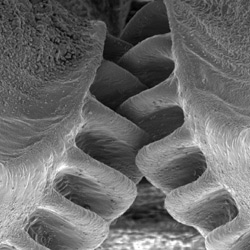
Let’s compare a gear train:
And, what is required informationally and organisationally to make the precise matching:
A moment’s reflection on such configurations will instantly tell us that there is an abstract space of possible configurations of the parts, scattered or clumped together, of which only a very few, proportionately, will rise above the floor of non-function to work as a fishing reel. Thus we see FSCO/I and the reason why it arises in deeply isolated, rare, islands of function in spaces of possibilities. For, well matched, correctly oriented, aligned and coupled parts must be brought together for functionality to result.
We can pause for a moment to speak to those who now wish to race off on side-tracks about how biological, cell based life reproduces and that renders the above irrelevant. The problem is, part of what is to be explained is that as von Neumann suggested, such cell based life uses FSCO/I-rich facilities, the von Neumann kinematic self-replicator, to achieve this capability:
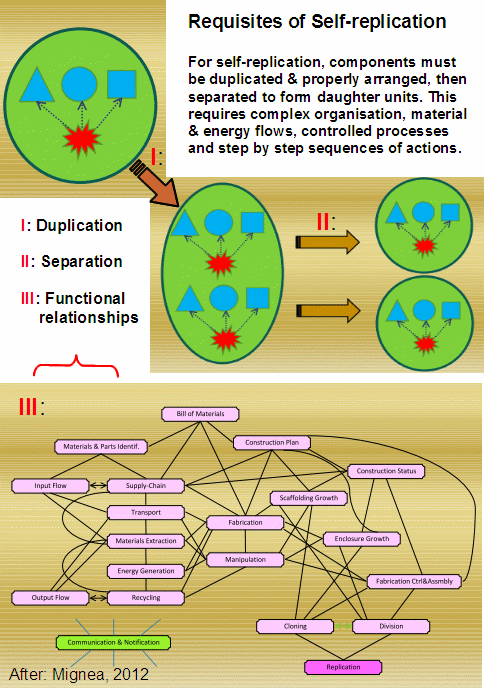
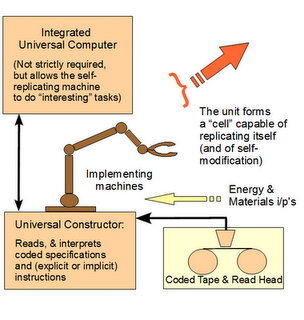In short, at OOL, the appeal to vNSR has to be addressed in terms of explaining the FSCO/I in it on precisely the sort of blind search challenge that has been discussed; credibly requiring 100 – 1,000 kbits of genetic information coupled to execution machinery and an encapsulated metabolic entity, which has to form in a plausible environment by blind processes demonstrated to be feasible per observation, not speculation or speculation on steroids by way of computer simulation. Then, to move on to explain the variety of major body plans, innovations of 10 – 100+ million bits of further information and associated systems has to be accounted for.
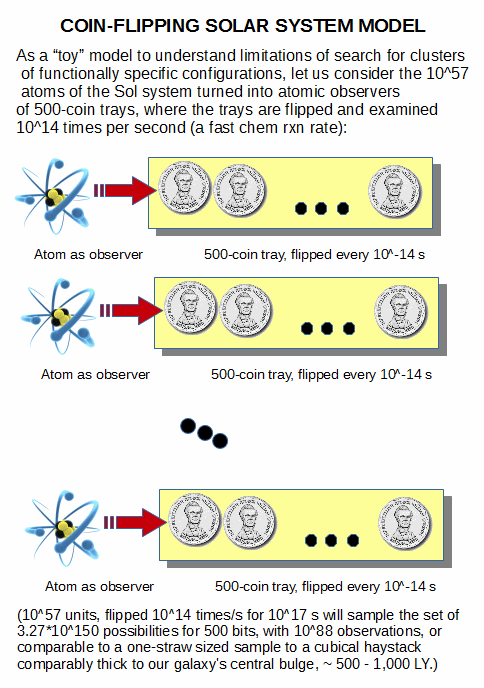
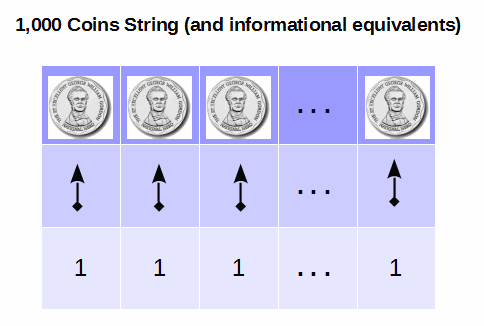
Where, just 500 – 1,000 bits of information correspond to configuration spaces of order 3.27*10^150 to 1.07*10^301 possibilities. And yes, we can here represent the search challenge in the very generous terms of the 10&57 atoms of our solar system or the 10^80 of the observed cosmos each making 10^14 [fast chemical reaction rate, especially for organic chemistry] observations of a tray of coins (or equivalently a paramagnetic substance) every second, for 10^17 s, comparable tot he time to the singularity:
(In short, we can readily see the emptiness of dismissive remarks on “big numbers” that too often appear in UD’s objector sites.)
The search challenge then becomes a matter of a space of possibilities explored through random walks (including dusted hops) and/or equally blind trajectories based on mechanical necessity. The target zones are islands of function out there in the space of possibilities corresponding of course to cell based life. The first challenge is to get to the shoreline of a first such island of function. Once there, presumably population variation and selection driven hill-climbing may operate within the island of function, subject to the problems of such hill climbing. But then, to move across to another island of function for a novel body plan, intervening seas of non-function will have to be crossed, precisely what hill-climbing is not applicable to. Where, no, it is not plausible that there is a grand continent of functionality, starting from the known scattering of protein fold domains in amino acid configuration space, a part of the whole situation.
We may freely illustrate:
And:
So, we may see that in an ID context informed by the AI approach of state space search (or more broadly, the underlying statistical mechanics approaches):
KF, :>>search . . . is tantamount to sampling from a configuration space.
[As, algebraic representation is commonly desired (and is often deemed superior to illustration or verbal description), a traditional representation of such a space is to symbolise it as Omega, here we can use w. Search then is obviously — and the obviousness is a material point here — tantamount to taking a subset of cases k in w by whatever relevant means, blind or intelligent. The search challenge then is to find some relevant zone z in w such that a performance based on configuration rises above a floor deemed non-functional: find/happen upon some z_i in w such that p(z) GT/eq f_min. Zones z are islands of function in the configuration space, w.]
In that context, the search problem is to solve the search challenge as identified, especially for large configuration spaces that exceed 10^150 – 10^300 possibilities, i.e. for 500 – 1,000 bits as a threshold. The answer to which is, that there is no credible solution by blind chance and/or mechanical necessity within the scope of the sol system to the observed cosmos. I add: intelligently directed configuration, using insight, routinely solves this problem, e.g. posts pro and con in this thread. The observed base of cases exceeds a trillion.
A search algorithm can be identified as attacking the search problem i/l/o the relevant possible searches, modulo the issue that there may be a need to intervene and impose a computational halt as some searches may run without limit if simply left to their inherent dynamics. Where, an algorithm is generally understood to be a finite, stepwise computational process that starts with a given initial point and proceeds to provide a result that is intended by its creator. This obtains for computation, which may model the real world situation which is dynamical rather than algorithmic.
I would consider that, given the context, search problems and algorithms are relatively trivial to understand, once search has been adequately conceptualised [and as above, further informed by the AI approach, state space search].>>
All of this then feeds into the reason why the design inference explanatory filter (here in successive, per aspect form) is credibly reliable in identifying cases of design as materially relevant cause, simply from observing FSCO/I:
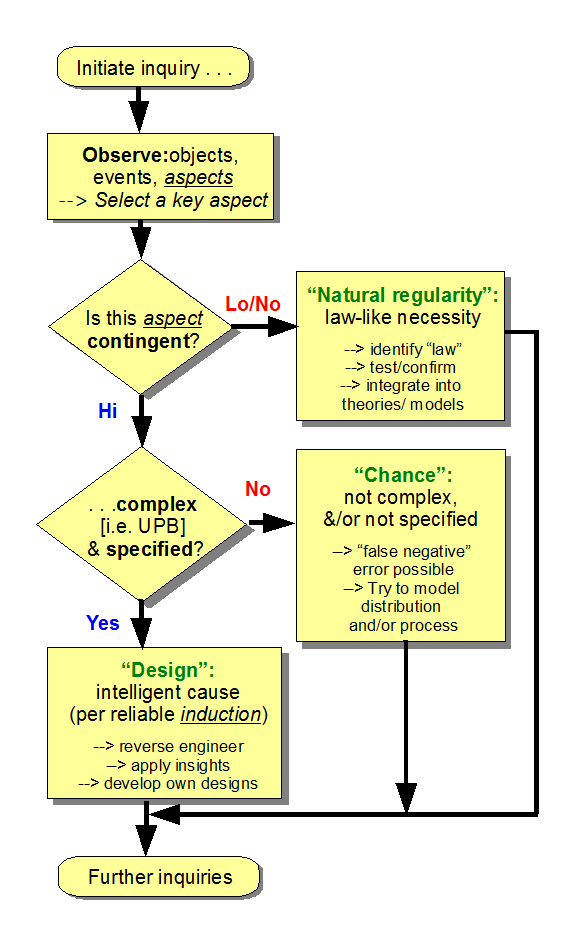For, the first decision step distinguishes highly contingent from low contingency situations, filtering off cases where mere mechanical necessity is the best explanation of a particular aspect. At the second decision node we filter off things of low complexity and also cases where the function is not of relevant type: specific, highly complex [thus a large configuration space], dependent on synergistic interaction of parts.
But what about specifying probabilities?
While in many cases this is an interesting exercise in mathematical modelling or analysis, it is not actually relevant to search challenge.
For, we may readily identify when a search is of excessive cost comparable to even the atomic resources of our solar system and/or the observed cosmos. Once complexity is beyond 500 – 1,000 bits, that is enough for our purposes. Under that scope of possibilities, the relevant resources cannot blindly search sufficient of the space to make any happening on a target seem plausible. If a target was hit under these circumstances, the best explanation per Newton’s vera causa principle of actually observed causes being used in scientific explanations, is active information conveying an implicit map or else intelligence that puts us down next to a target zone/ island of function or else a golden search that must be similarly selected with insightful knowledge of the possibilities.
So, we have excellent reason to freely conclude that the basic design inference and underlying frame of thought — never mind all sorts of objections that have been made or that will continue to be made — are well-founded. But those objections are so persistent that it is sometimes necessary to take a sledgehammer to a cashew nut. END