(Follows up from here.)
Over at MF’s blog, there has been a continued stream of objections to the recent log reduction of the chi metric in the recent CSI Newsflash thread.
Here is commentator Toronto:
__________
>> ID is qualifying a part of the equation’s terms with subjective observation.
If I do the same to Einstein’s, I might say;
E = MC^2, IF M contains more than 500 electrons,
BUT
E **MIGHT NOT** be equal to MC^2 IF M contains less than 500 electrons
The equation is no longer purely mathematical but subject to other observations and qualifications that are not mathematical at all.
Dembski claims a mathematical evaluation of information is sufficient for his CSI, but in practice, every attempt at CSI I have seen, requires a unique subjective evaluation of the information in the artifact under study.
The determination of CSI becomes a very small amount of math, coupled with an exhausting study and knowledge of the object itself.>>
_____________
A few thoughts in response:
a –> First, let us remind ourselves of the log reduction itself, starting with Dembski’s 2005 chi expression:
χ = – log2[10^120 ·ϕS(T)·P(T|H)] . . . eqn n1
How about this (we are now embarking on an exercise in “open notebook” science):
1 –> 10^120 ~ 2^398
2 –> Following Hartley, we can define Information on a probability metric:
I = – log(p) . . . eqn n2
3 –> So, we can re-present the Chi-metric:
Chi = – log2(2^398 * D2 * p) . . . eqn n3
Chi = Ip – (398 + K2) . . . eqn n4
4 –> That is, the Dembski CSI Chi-metric is a measure of Information for samples from a target zone T on the presumption of a chance-dominated process, beyond a threshold of at least 398 bits, covering 10^120 possibilities.
5 –> Where also, K2 is a further increment to the threshold that naturally peaks at about 100 further bits . . . . As in (using Chi_500 for VJT’s CSI_lite):
Chi_500 = Ip – 500, bits beyond the [solar system resources] threshold . . . eqn n5
Chi_1000 = Ip – 1000, bits beyond the observable cosmos, 125 byte/ 143 ASCII character threshold . . . eqn n6
Chi_1024 = Ip – 1024, bits beyond a 2^10, 128 byte/147 ASCII character version of the threshold in n6, with a config space of 1.80*10^308 possibilities, not 1.07*10^301 . . . eqn n6a . . . .
Using Durston’s Fits from his Table 1, in the Dembski style metric of bits beyond the threshold, and simply setting the threshold at 500 bits:
RecA: 242 AA, 832 fits, Chi: 332 bits beyond
SecY: 342 AA, 688 fits, Chi: 188 bits beyond
Corona S2: 445 AA, 1285 fits, Chi: 785 bits beyond . . . results n7
The two metrics are clearly consistent . . . .one may use the Durston metric as a good measure of the target zone’s actual encoded information content, which Table 1 also conveniently reduces to bits per symbol so we can see how the redundancy affects the information used across the domains of life to achieve a given protein’s function; not just the raw capacity in storage unit bits [= no. of AA’s * 4.32 bits/AA on 20 possibilities, as the chain is not particularly constrained.]
b –> In short, we are here reducing the explanatory filter to a formula. Once we have specific, observed functional information of Ip bits, and we compare it to a threshold of a sufficiently large configuration space, we may infer that the instance of FSCI (or more broadly CSI) is sufficiently isolated that the accessible search resources make it maximally unlikely that its best explanation is unintelligent cause by blind chance plus mechanical necessity. Instead, the best, and empirically massively supported causal explanation is design:
Fig 1: The ID Explanatory Filter
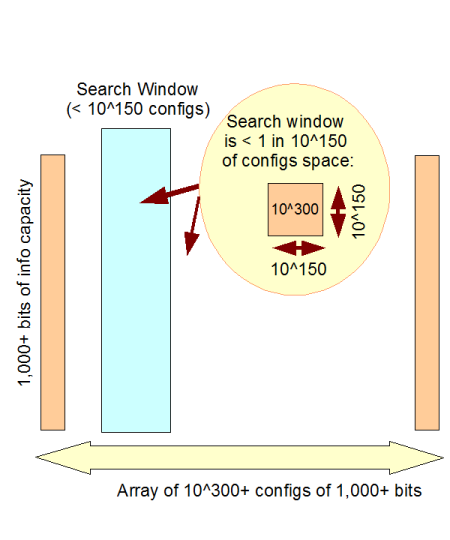
c –> This is especially clear when we use the 1,000 bit threshold, but in fact the “practical” universe we have is our solar system. And so, since the number of Planck time quantum states of our solar system since the usual date of the big bang is not more than 10^102, something that is in a config space of 10^150 [500 bits worth of possibilities] is 48 orders of magnitude beyond that threshold.
d –> So, something from a config space of 10^150 or more (500+ functionally specific bits) is on infinite monkey analysis grounds, comfortably beyond available search resources. 1,000 bits puts it beyond the resources of the observable cosmos:
Fig 2: The Observed Cosmos search window
e –> What the reduced Chi metric is telling us is that if say we had 140 functional bits [20 ASCII characters] , we would be 360 bits short of the threshold, and in principle a random walk based search could find something like that. For, while the reduced chi metric is giving us a value, it tells us we are falling short and by how much:
Chi_500(140 bits) = 140 – 500 = – 360 specific bits, within the threshold
f –> So, the Chi_500 metric tells us instances of this could happen by chance and trial and error testing. Indeed, that is exactly what has happened with random text generation experiments:
One computer program run by Dan Oliver of Scottsdale, Arizona, according to an article in The New Yorker, came up with a result on August 4, 2004: After the group had worked for 42,162,500,000 billion billion monkey-years, one of the “monkeys” typed, “VALENTINE. Cease toIdor:eFLP0FRjWK78aXzVOwm)-‘;8.t” The first 19 letters of this sequence can be found in “The Two Gentlemen of Verona”. Other teams have reproduced 18 characters from “Timon of Athens”, 17 from “Troilus and Cressida”, and 16 from “Richard II”.[20]
A website entitled The Monkey Shakespeare Simulator, launched on July 1, 2003, contained a Java applet that simulates a large population of monkeys typing randomly, with the stated intention of seeing how long it takes the virtual monkeys to produce a complete Shakespearean play from beginning to end. For example, it produced this partial line from Henry IV, Part 2, reporting that it took “2,737,850 million billion billion billion monkey-years” to reach 24 matching characters:
- RUMOUR. Open your ears; 9r"5j5&?OWTY Z0d…
g –> But, 500 bits or 72 ASCII characters, and beyond this 1,000 bits or 143 ASCII characters, are a very different proposition, relative to the search resources of the solar system or the observed cosmos.
h –> That is why, consistently, we observe CSI beyond that threshold [e.g. Toronto’s comment] being produced by intelligence, and ONLY as produced by intelligence.
i –> So, on inference to best empirically warranted explanation, and on infinite monkeys analytical grounds, we have excellent reason to have high confidence that the threshold metric is credible.
j –> As a bonus, we have exposed the strawman suggestion that the Chi metric only applies beyond the threshold. Nope, it applies within the threshold and correctly indicates that something of such an order could come about by chance and necessity within the solar system’s search resources.
k –> is a threshold metric inherently suspicious? Not at all. In control system studies, for instance, we learn that once you reduce your expression to a transfer function of form
G = [(s – z1)(s- z2) . . . ]/[(s – p1)(s-p2)(s – p3) . . . ]
. . . then, if poles appear in the RH side of the complex s-plane, you have an unstable system.
l –> A threshold, and one that, when poles approach close to the threshold from the LH half-plane, will show up in a tendency that can be detected in the frequency response as peakiness.
m –> Is the simplicity of the math in question, in the end [after you have done the hard work of specifying information, and identifying thresholds], suspicious? No, again. For instance, let us compare:
n –> Each of these is elegantly simple, but awesomely powerful; indeed, the last — precisely, a threshold relationship — was a key component of Einstein’s Nobel Prize (Relativity was just plain too controversial). And, once we put them to work in practical, empirical situations, each of them ” . . . is no longer purely mathematical but subject to other observations and qualifications that are not mathematical at all.”
(The objection is clearly selectively hyperskeptical. Since when was an expression about an empirical quantity or situation “purely mathematical”? Let’s try another expression:
How are its components measured and/or estimated, and with how much application of judgement calls, including those tracing to GAAP? [Cf discussion here.] Is this expression therefore meaningless and of no utility? What about M*VT = PT*T?)
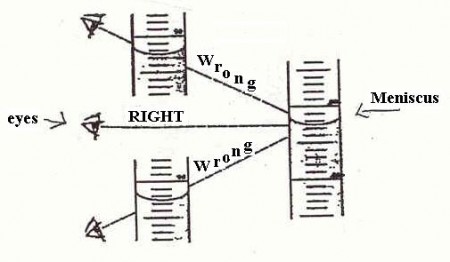
o –> So, what about that horror, the involvement of the semiotic, judging agent as observer, who may even intervene and– shudder — judge? Of course, the observer is a major part of quantum mechanics, to the point where some are tempted to make it into a philosophical position. But the problem starts long before that, e.g. look at the problem of reading a meniscus! (Try, for Hg in glass, and for water in glass — the answers are different and can affect your results.)
Fig 3: Reading a meniscus to obtain volume of a liquid is both subjective and objective (Fair use clipping.)
p –> So, there is nothing in principle or in practice wrong with looking at information, and doing exercises — e.g. see the effect of deliberately injected noise of different levels, or of random variations — to test for specificity. Axe does just this, here, showing the islands of function effect dramatically. Clipping:
. . . if we take perfection to be the standard (i.e., no typos are tolerated) then P has a value of one in 10^60. If we lower the standard by allowing, say, four mutations per string, then mutants like these are considered acceptable:
no biologycaa ioformation by natutal means
no biologicaljinfommation by natcrll means
no biolojjcal information by natiral myans
and if we further lower the standard to accept five mutations, we allow strings like these to pass:
no ziolrgicgl informationpby natural muans
no biilogicab infjrmation by naturalnmaans
no biologilah informazion by n turalimeans
The readability deteriorates quickly, and while we might disagree by one or two mutations as to where we think the line should be drawn, we can all see that it needs to be drawn well below twelve mutations. If we draw the line at four mutations, we find P to have a value of about one in 10^50, whereas if we draw it at five mutations, the P value increases about a thousand-fold, becoming one in 10^47.
q –> Let us note how — when confronted with the same sort of skepticism regarding the link between information [a “subjective” quantity] and entropy [an “objective” one tabulated in steam tables etc] — Jaynes replied:
“. . . The entropy of a thermodynamic system is a measure of the degree of ignorance of a person whose sole knowledge about its microstate consists of the values of the macroscopic quantities . . . which define its thermodynamic state. This is a perfectly ‘objective’ quantity . . . it is a function of [those variables] and does not depend on anybody’s personality. There is no reason why it cannot be measured in the laboratory.”
r –> In short, subjectivity of the investigating observer is not a barrier to the objectivity of the conclusions reached, providing they are warranted on empirical and analytical grounds. As has been provided for the Chi metric, in reduced form. END