By Robert Deyes And John Calvert
PART I: FOUNDATIONS IN PROBABILITY
“We call these [mutation] events accidental; we say that they are random occurrences. And since they constitute the only possible source of modifications in the genetic text, itself the sole repository of the organism’s hereditary structures, it necessarily follows that chance alone is at the source of every innovation, of all creation in the biosphere. (Jacques Monod)[Ref 1]
Many in science employ a dogma that life is related to matter, rather than to mind. The dogma seems conceptually flawed. Unlike rocks, rivers, wind, rain and snow, life operates on information – tightly integrated messages that function to order a grand symphony of future events for clearly evident purposes. Lacking a mind, matter simply can’t comprehend or order future events for a purpose. Because purpose only derives from mind, logic seems to demand that life is related to mind rather than just to matter.
Lacking a mind, material causes have only two tools to work with: (1) physical and chemical necessity flowing from the properties of matter, energy and the forces and (2) chance. As implied by Monod’s statement, physical and chemical necessity are not tools used to order the symbol sequences that make life. Hence, the heavy lifting is left to chance by default.
The chance default is considered adequate because it is endowed with seemingly gargantuan resources consisting of billions of years of time and countless opportunity. The purpose manifested by life is only “apparent” and not objectively real because chance can explain it. For the materialist, the purpose apparent in the messages of life is just an illusion, like the illusion of a rising sun in the morning.
This article explains why Monod is wrong and the claim of chance fails. It fails because probability decreases exponentially at an accelerating rate as the complexity of a system increases only incrementally. Because of the phenomenal rate of reduction even billions and billions of years of time and opportunity are not adequate for chance to mimic the simplest functions of life.
If chance is not adequate to explain life, given the absence of chemical necessity for its purposeful character, it seems we have no excuse for not relating life to mind, rather than to matter.
A Game Of Relationships (A vignette illustrating the implausibility of functional relationships arising by chance):
Today is a great day because Maggie is visiting. Maggie is your five year-old grand daughter. She brings with her a new game her dad gave her called “Relationships.” The game includes an easel that you set up in the family room. It also has a white metal drawing board that sits on the easel. The board is ten inches square and is divided by very faint white lines into 100 squares as follows:

The metal board is magnetic. Hanging below the cross bar of the easel is a box. Inside the box are little metal discs. Painted on each disc is an upper case or lower case letter of the 26 letter alphabet, a period, a comma or a question mark. Thus, there are 55 different symbols in the box. With these symbols one can make all manner of patterns.
A little machine is attached to the box. Every six minutes the machine randomly pulls a disc out of the box and randomly puts it on one of the 100 squares on the drawing board. After it does this it replenishes the box with a like copy of the placed disc so the box always has a full set of the 55 letters and punctuation marks.
Because the board is magnetic, the iron discs stick without falling to the floor. You and Maggie turn the machine on and watch it draw the letter “D” and put it in row 2 of column 4. You then retire to the kitchen for some milk and cookies. A few minutes later, you go back to the family room and see that there is now a second letter on the board. A letter “T” is in row 5 of column 3:

Dependent Physical Relationships
The point of the game is to describe the relationships that appear on the board. So, you and Maggie start looking for relationships. You find that there is a dependent or necessary relationship between the discs and the magnetic board. In other words, if you put a disc close to the board an electromagnetic force contained in the atoms that make up the board strongly attract the atoms that make up the iron disc. But if you release the disc before it gets too close to the board it will be pulled by the gravitational force to the ground. So, you conclude that the discs are related to the board by chemical and physical necessity. Stated another way, the relationship of the letter D to the board is dependent on the electromagnetic attraction of the board. The combination of the metal properties of the discs and the magnetic property of the board produce this “necessary” or dependent relationship between the board and the discs. If the discs were made of wood they would not stick. Instead, you would find them scattered on the floor unrelated to the board.
Independent Physical Relationships
Maggie likes playing with the magnets, but is getting bored. So, you ask her if there is a relationship between the letters themselves. Is the letter “D” related to the letter “T”? Both are related to the board. But, are they related to each other? You show Maggie how there is no physical or chemical necessity for D to be in row 2 of column 4 or for the T to be in row 5 column 3. Also, there is no necessity for the “D” to be a “D” or the “T” to be a “T”. They could easily be “A’s”, “c’s” or “q’s”. Thus there is no physical, chemical or “necessary” relationship between the “D” and “T”. It can also be said that “D’s” relationship in space does not depend on “T’s” relationship in space. They are independent of each other. You also know that the machine is a random generator. It just pulls and puts symbols randomly. So, if the discs are related at all, it is simply a random or “chance” relationship. Their relationship to the board is necessary, but their relationship to each other is random.
Functionally dependent relationships
Maggie says she has had enough and wants to go out and play. So she goes outside and you go back to the kitchen to make a pie for dinner. After putting the pie in the oven, you stroll back into the family room to watch the news. Now you see a new pattern of letters on the board that spells “Think.”
With some surprise, you ask again – what is the relationship, if any between the discs? Although there is no physically dependent relationship between the “T” and the “D,” there is a clear relationship between the “T” and each of the other four letters that comprise the word “Think.” By themselves they are meaningless. Together the discs function to produce an event to occur in the future. The future event is the manifestation of the meaning symbolized by the command “Think.” Once all five of the letters are assembled in that precise sequence there comes into existence a manifestation of meaning symbolized by the word “Think.” That meaning is of course:
“to employ one’s mind rationally and objectively in evaluating or dealing with a given situation.”
Consider the following arrangements on a board:
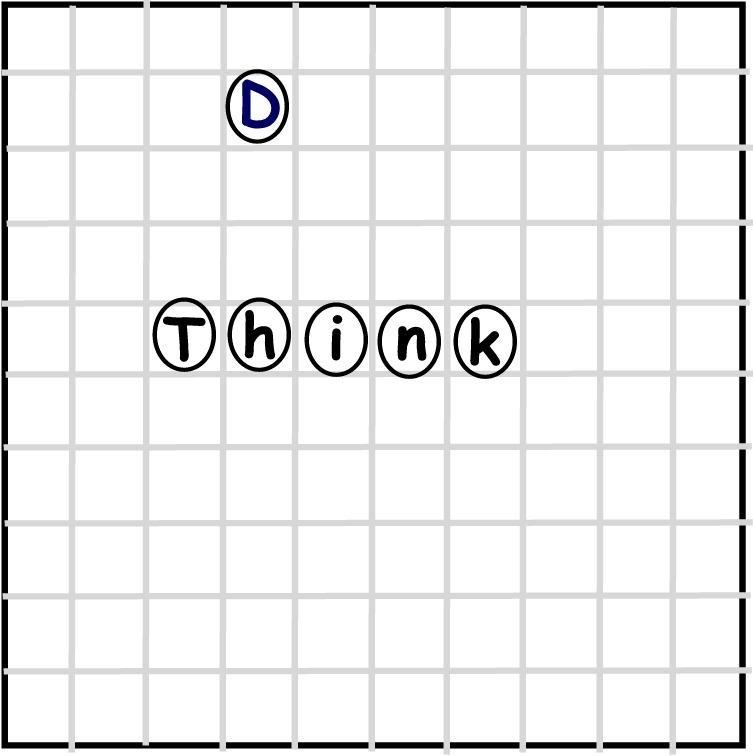
If any of the five letters were missing or on the wrong square the manifestation would not occur. Hence, all discs are related to each other by a non-physical intangible unique function. Although the discs are physical objects themselves, the function their relationship manifests is not physical. You also note that while the relationship between the discs and the board is necessary or dependent due to the charge on physical particles – atoms and electrons, the relationships between each of the letters in Think are physically independent, unified only by an intangible function.
“Function” is synonymous with “meaning,” and “purpose,”
You ask, what can produce a “functional,” “meaningful,” or “purposeful” relationship?
Just as a magnetic relationship can derive only from an electromagnetic force, a purposeful relationship can only derive from a mind or some form of intelligence that has the capacity to think of it. Purpose, meaning or function can only be a derivative of thought. It is produced in the mind through the capacity of the mind to “know” the present, store that “knowledge” in memory, to “think” about that knowledge so as to “predict” the future and to then “choose” to alter the future for an intended purpose. The arrangement of matter, energy and the forces to achieve the purpose per the choice, becomes the manifestation of that immaterial thought or purpose born in the mind.
Material causes and random processes, which lack a mind, simply do not have the capacity to produce an intention in the first instance. Material causes cannot know or think. Hence, they lack the capacity to manifest thoughts they cannot have. They can’t know the present, have knowledge of the past or choose to alter the future.
Accordingly, if a function is manifested by a pattern consisting of physically independent elements, then it is reasonable to infer that a mind may have produced it.
Think of how a mind produces the future manifestation associated with the word “Think.” The mind orders a sequence of steps integrated to manifest a function that does not come into being until all the steps have been taken. For example, the first step in the production of the manifestation of a command to think is to generate the letter “T.” That step alone is not sufficient to produce the manifestation. A second step must also be taken – the placement of an “h” immediately to the right of the “T.” But that does not produce the manifestation either. Three more steps are required. The future effect does not arise until the last letter is placed. The only cause that we know of that has the capacity to generate and then manifest a real intention is a mind.
Minds order events for a future purpose. They order patterns that will command, inform, assemble, build, enable, excite, please, transport, house, nourish, and destroy. Each manifestation of a mind is preceded by a set of steps. The steps often reveal the ultimate intention of the mind, but not always. One does not know the true intention of the minds that built Stonehenge. However, one may know that it was produced by a mind or minds for a purpose. One may not know the purpose of a homicide, although one may reasonably infer that it was a homicide. The inference to a mind arises from the clues left behind by the mind – the physical steps that had to be taken to produce the intended non-physical function or effect.
The name we often ascribe to a pattern that manifests the intention of a mind is “information.” Information is clearly carried in writings which serve to expressly reflect intentions. It is not always apparent in all mind produced patterns, such as works of art, ciphers, incomplete works or works that use an unintelligible language.
Who or what “done” it? So, when you see “Think” on the board you scratch your head and think. You are the only one who has been in the house since Maggie went out to play. If that is true, then no mind has been present to fiddle with the random generator. Perhaps the discs that spell “Think” are not a derivative of intention but are in fact just related by chance. Maybe the manifestation of meaning reflected in the sequence is just an illusion of a mind at work. If chance can explain the pattern, then you need not look for Maggie hiding in the closet.
You think chance ought to be a plausible alternative. After all, there are only five letters involved in the pattern. Chance ought to be able to account for such a short sequence. So you decide to calculate the odds to show how chance can explain the pattern and solve the mystery.
The probability (P) of the occurrence of a series of events comprising a pattern manifesting a particular function (F) is the number of opportunities or trials (T) for the pattern to occur divided by the number of possible patterns or outcomes (O) that could occur or PF=T/O:
T number of trials for function
PFprobability of function = ————————————-
O possible outcomes
A simple example would be the probability of the occurrence of a single event pattern consisting of a dot that could be produced by flipping a coin that has a dot on one side and a dash on the other. The probability of getting the pattern of single dot on one trial consisting of one flip is:
Although the numerator remains 1, a crucial change occurs in the denominator. The number of outcomes or possible patterns in the denominator grows at an exponential rate as the complexity of the target pattern increases. The first flip makes possible two outcomes (dot or dash), the second four (dot dot, dash dash, dot dash or dash dot), and the third eight (2x2x2 = 8). What we find is that the numerator remains constant at one, with each increase in sequence complexity, requiring a serial multiplication in the number of possible outcomes:
T (1 trial of 3 flips)
PFprobability of function = —————————— = 0.125
O (2x2x2)
Suppose the desired function is the message “help” to be spelled out in Morse code language using three dots, three dashes and three dots. In this case, the number of trials remains one, but the nine steps needed to get to function requires nine flips of the two sided coin. Thus the number of outcomes provided by each flip, being 2, must be serially multiplied by each other so that the number of possible outcomes becomes 2x2x2x2x2x2x2x2x2= 29 =512. So the probability is 1/512 = .0019.
First 9 flips = 1/512
Flip 10 = 2×512= 1/1,024
Flip 11 =2×1,024= 1/2,048
Flips 12-17…….…… = 1/131,072
Flip 18 =2×131,072= 1/262,144
Flip 19 =2×262,144= 1/524,288
Flip 20 =2×524,288= 1/1,048,576
Flip 21 =2×1,048,576= 1/2,097,152
Flip 22 =2×2,097,152= 1/4,194,304
Notice how probability declines exponentially due to the concomitant exponential increase in the number of outcomes. Consider our earlier equation:
T number of trials for function
PFprobability of function = ——————————————
O possible outcomes
The number below the line is important, because it tells you the number of trials you would realistically have to put in the numerator – above the line – to get to a probable outcome. If the denominator calls for 8 outcomes, then you need 8 trials for the event to be probable. If the denominator calls for 4 million outcomes you need 4 million trials. But what if you don’t have enough time or resources to run 4 million trials? If you could do ten 22 flip trials in an hour it would take 48 years of constant flipping to expect a random generator to send a functional message that might get help to John. By then it would be too late.
So, armed with this basic knowledge of probability theory, you ask, what is the chance of the “T”, “h”, “i,” “n,” and “k” being pulled and then put in the correct positions in Maggie’s ‘Relationship’ game? The number of possible pull outcomes consists of 55 since there are always 55 different letters in the box. The number of possible put outcomes are 100 since there are 100 different squares on which any letter may be placed. Thus, the number of possible outcomes for any pull-put step is 55 x 100 = 5,500. However five pull-put steps are required for one trial. The number of possible outcomes for one five step trial is 5,500 x 5,500 x 5,500 x 5,500 x 5,500 = 5,032,843,750,000,000,000. So the probability is one over 5 trillion trillion:
T: 1/5,500
Th: 1/5,500 x 1/5,500 = 1/30,350,000
Thi: 1/5,500 x 1/5,500 x 1/5,500 = 1/166,375,000,000
Thin: 1/5,500 x 1/5,500 x 1/5,500 x 1/5,500 = 1/915,062,500,000,000 (915 trillion)
Think: 1/5,500 x 1/5,500 x 1/5,500 x 1/5,500 x 1/5,500 = 1/5,032,843,750,000,000,000 (5 trillion trillion)
When does improbability equate to practical impossibility? As one looks at the gargantuan number – one over 5 trillion, trillion, one could argue that even with such low probability, it is still possible that “Think” just might appear on the first trial – its possible. But the question is, can we reasonably expect a chance process to produce a specified or needed effect within a given amount of time? If not, then it is unreasonable for us to rely on the chance process to produce the effect. In our example the robot is only pulling letters at the rate of ten an hour. Suppose the board is automatically cleared after each five pulls. Only two five sequence trials an hour are now permitted. To expect “Think” to arise by chance would take 2.5 trillion, trillion hours or 574 trillion years. The universe is only 14 billion years old. By adding trillions of robots we could maybe get within the age of the universe, but who would be around to “think,” after the production of the message? Given these odds, it is not reasonable for us to attribute the apparently meaningful command of “Think” to chance rather than to a mind.
Imagine a safe cracker that has only six hours in the middle of the night to open the bank vault having a combination lock with 100 set points and a combination that requires the knob to be turned to three correct numbers in sequence. Each trial consists of three turns. The possible number of outcomes is 1/100 x 1/100 x 1/100 = 1/1,000,000. If it takes a minute to do each three turn trial, we could realistically expect the robber to take 16,667 hours to open the safe. He only has six. A combination lock could be made with 1,000 set points and require ten turns to the correct number. But, as a practical matter that extra degree of complexity is not needed. Combination locks reflect the amount of complexity needed to establish practical impossibility within a specified time.
Mathematician William Dembski argues that anything less probable than one over 10150 is statistically impossible as a practical matter (Refs 2-3). The number is based on the number of elemental particles in the universe (electrons, protons and neutrons) which is about 1080 , multiplied by the number of times an elemental particle changes state within a second, which is 1045, multiplied by the number of seconds which have elapsed since the beginning of the universe, assuming it arose about a billion times 20 billion years ago, which is 1025 seconds ago (1080x1045x1025=10150). The number 10150 quantifies all of the time and opportunities – probability resources – available in the entire universe for any given sequence of past events to have occurred by chance. It represents the largest number that one could put in the numerator for any set of events within this universe. The number is helpful, because it can be used to assess whether it is reasonable to round the probability of an event to zero, as a practical matter.
For example, assume every elemental particle in the universe was a monkey flipping coins at the rate of 1045 flips a second. Could we reasonably expect them to produce a sequence of heads and tails that would match the first sentence in Lincoln’s Gettysburg Address in Morse code?
“Four score and seven years ago, our fathers brought forth upon this continent a new nation, conceived in liberty, and dedicated to the proposition that all men are created equal.”
The sentence contains 177 letters, spaces and punctuation marks. It can be sent with a 577 symbol sequence of dots and dashes in Morse code. The probability is 1 over 2577, which is the same as 1 over 10173. Since the 10173 number is significantly less probable than the universal probability limit of 10150, a reasonable person would not bet on the monkeys, even if they started flipping at the beginning of the universe.
As you return to the word “Think” on Maggie’s game board and think of the odds of one over five trillion, trillion, you conclude that it is not reasonable to believe that the relationship between the five letters was ordered just by chance. While 1/5,032,843,750,000,000,000 does not exceed the 1/10150 discussed above, there just has not been enough time in the known universe assuming that the robot is pulling letters at the rate of ten an hour. You also know that physics doesn’t order the sequence. Physics and chemistry can order the relationship between the discs and the board but they can’t order the relationship between the discs themselves to require that they manifest the word “Think.”
So, you think somehow Maggie must have snuck into the room and fiddled with the discs while you were making the pie. Isn’t it amazing how smart a five year old grand child can be!
In summary, this vignette illustrates the inherent problem of attributing complex functional sequences to chance. As the complexity of the sequence increases, its chance probability decreases exponentially. Within finite realms, chance losses its plausibility with only small increases in complexity.
ABOUT THE AUTHORS
Robert Deyes holds a Masters Degree in Medical Genetics from the University of Glasgow and a Bachelors Degree in Molecular Biology from the University of Portsmouth, UK. He carried out an 18-month research project at the Université Louis Pasteur in Strasbourg, France. John Calvert, JD, holds a Bachelors degree and professional experience in Geology and is Managing Director of Intelligent Design Network Inc, a non-profit organization that seeks institutional objectivity in origins science.
BIBLIOGRAPHY
1. Jacques Monod, Chance and Necessity, pp 112-3 (Vintage Books 1971); Molecular Biologist known for his work on gene expression in the Lac Operon. Nobel Prize in Physiology
2. William Dembski in The Design Inference: Eliminating Chance Through Small Probabilities, p.36 et. seq (Cambridge Press, 1998)
3. William Dembski in No Free Lunch: Why Specified Complexity Cannot Be Purchased Without Intelligence, p.83 (Rowman & Littlefield, 2002)