For some weeks now, an underlying persistent debate on the reality of numbers has emerged in several discussion threads at UD. In part, it has been cast in terms of nominalism vs platonic realism; the latter being the effective view of most working mathematicians. Obviously, this is a first principles issue and is worth focussed discussion.
Now, No. 14 in this series, on objectivity of aesthetics principles as canons of beauty, begins by pointing to an underlying challenge:
We live in a Kant-haunted age, where the “ugly gulch” between our inner world of appearances and judgements and the world of things in themselves is often seen as unbridgeable. Of course, there are many other streams of thought that lead to widespread relativism and subjectivism, but the ugly gulch concept is in some ways emblematic. Such trends influence many commonly encountered views, most notably our tendency to hold that being a matter of taste, beauty lies solely in the eye of the beholder.
Of course, F H Bradley, long since pointed out that to claim the un-know-ability of things in themselves is already to claim a major point of just such knowledge. So, this is self-referentially absurd. Wisdom, then, is to acknowledge that we can and do err but even that is a point of undeniably certain knowledge therefore we can and do confidently know some aspects of reality as it is, not just as it appears to us. Reality is in part intelligible, it is not utterly inscrutable. Already, this is a hint that there is a rational . . . a logical . . . structure to being which rational creatures may seek to understand, succeeding part of the time. Where of course aspects of that structure will be quantitative.
Let me highlight the core argument (and pardon the inflexibility of the new block style WP is using):
>>to assert that in effect conceptualism about abstracta is true, one relies on abstracta being in reality, e.g. here that a description or assertion can hold a relationship of accurate description with things as they are. Absent the reality of such a relationship independent of our individual or collective concepts, truth is meaningless. If only the concrete exists in reality, truth, an abstract relationship using symbolic representation (other abstracta!) is a case of non-being, illusion. Actually, illusion is another abstract relationship. Meaninglessness is next up, but this too is an abstract state of affairs. The infinite regress of abstracta begging to be acknowledged as real yawns open.
The reality of core abstracta is inescapably the case, i.e. it is necessarily true on pain of not being able to think, communicate conceptually, reason [implication is abstract], speak truth, demonstrate, warrant, know etc.
The serious issue then follows: in what way are such things real?
The best I can answer for now is that such abstracta are connected to the logic of being for worlds or things in the world. They are logically relevant characteristics of being, which in many cases are shared across beings as archetypes that are in-common, or even are in-common across possible worlds. In some cases such as numbers they are in common to all possible worlds as part of the fabric of any distinct possible world.
We may recognise or discover them and try to identify what they precisely are, but in many cases they defy particular definition in words.
Where do they come from, where are they? They come from the logic of being and are embedded as constraints on being. For instance, no entity E is such that it has two core characteristics x and y where y = ~x.
That is why square circles are impossible of being. Regardless of how we may form a fuzzy imagination that oscillates between the shapes or may try to superpose and blend the two.

Thus, abstracta are part of the distinct identity, nature and being of any particular entity. That is, the principle of distinct identity has ontological, not just conceptual, significance. That’s why we recognise it as a first principle of right reason.
So, not a spooky, mysterious, metaphysical world of forms, just the architecture of — rational principles or “logic” of — being or possible being (and of impossibility of being). Where of course a considerable part of that embedded architecture of being is structural and quantitative. That is, Mathematical. Mathematics has in key part ontological import. Hence, Wigner’s point on its astonishing power. The music of the spheres is written in the language of mathematics, with — I daresay — Fourier leading the charge.>>
Fourier in action:
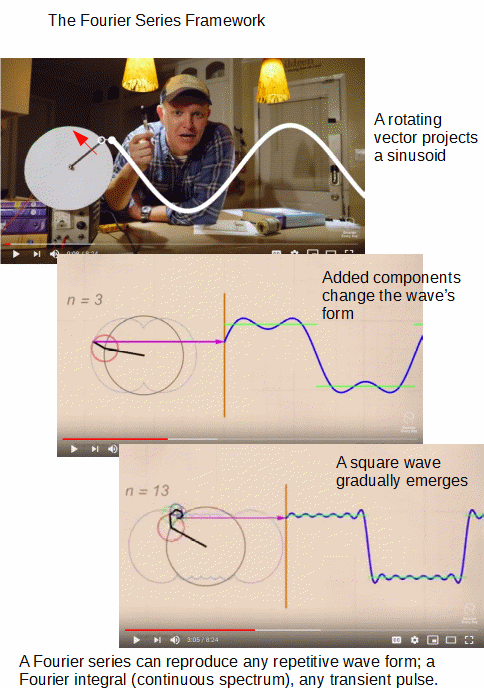
And again (a mechanical implementation in our hearing . . . relevant to octaves and fifths in music etc):
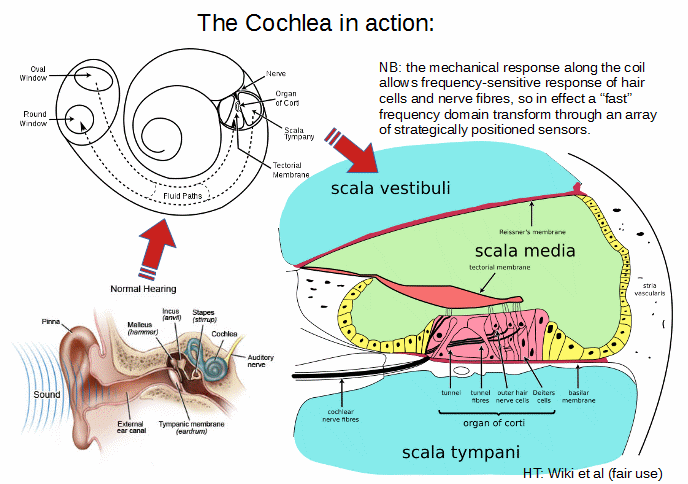
Let me then set it in the context of an ongoing exchange in the thread on beauty, and I take liberty to headline comment 390:
KF, 390: >>H, Let’s roll the tape a bit:
H, 377: >>kf writes,
What happens in the worldis independent of[–> antecedent to and insofar as it is intelligible, influences] our thoughts about it [which thoughts in many cases may and do accurately describe reality, concrete and abstract.”
I’ll agree that the world is antecedent to our thoughts: we experience the world and then form thoughts about.
I’ll agree that “insofar as it is intelligible, [the world] influences our thoughts about it, which thoughts in many cases may and do accurately describe reality,concreteand abstract” [sorry, WP suppressed strike-throughs]>>KF, 378: >>H, that apparent rejection of the reality of certain abstracta, if so, is fatally self-referential for much the same reason as nominalism (which is a form of such rejection) fails.>>
H, 379: >>I’ve explained my position, and see nothing “fatally self-referential” in it. The world is intelligible, and we are intelligent, so our understandings provide reasonably accurate maps of the world. We use abstractions to describe the world, but the world itself is “concrete” in the sense that it is its behavior which we observe that is the source of the material for our abstractions.
Probably no need for you (or me) to repeat ourselves again (although I do have a new thought on the matter that I may share later in the day when I have some time.)>>KF, 380: >>when an objective matter is on the table, agreement or disagreement is immaterial. Just to make statements you have had to repeatedly rely on abstracta being the case not just perceptions. Indeed, truth is an abstract relationship of statements to what is the case, belief or disbelief, agreement or disagreement too. The reality of core abstracta is inescapable.>>
H, 381: >> I have clearly said that we use abstractions – we have to – just to talk about the world, so of course I agree with you when you write, “Just to make statements you have had to repeatedly rely on abstracta being the case not just perceptions.” Perceptions of the world bring in the data from which we create our abstractions, but abstractions are a necessary, central aspect of our ability, as rational, logical creatures, to understand the world.
Is this the point upon which you think my position is “fatally self-referential”?, because if so it misrepresents me. Perhaps you could explain more about your “fatally self-referential” statement.>>KF, 382: >>this begins to approach the inescapability of the laws of thought, which embed cases in point. To attempt to deny one is forced to accept implicitly. For instance, you are affirming or implying that somethings are true, are accurate descriptions of reality, which is itself an abstract relationship, indeed the words and what they represent involve abstract relations. That is telling us something — we are at a start-point.>>
H, 383: >>Yes, I have continually said that we use abstract concepts to make statement about reality that are, to various degrees, accurate descriptions.>>
KF, 386: >>we cannot escape core abstracta and they are inescapably true or real as appropriate.>>
H, 389: >>kf writes “that apparent rejection of the reality of certain abstracta, if so, is fatally self-referential.” I accept the reality of the abstract concepts we create that describe the reality we experience. How is that “fatally self-referential”? I don’t see how you have explained that.>>
Notice, how you repeatedly affirm certain things to be true, i.e. to actually accurately describe real states of affairs? That is itself an abstract relationship, which must be real albeit abstract or discussion collapses. Likewise, the Mobius strip’s behaviour pivots on how it has ONE edge, ONE surface, etc. So if by cutting we introduce one or two further edges, it will form a longer loop or two interlocked loops. One-ness, two-ness, three-ness and consequences on the logic of being are abstract but take effect in space and bodies. It does so independent of our thoughts, concepts, expectations, as the relevant abstract properties are part of its core characteristics.
Above, at 375, I again laid out a demonstration as to why numbers are necessary entities that will manifest in any possible world, antecedent to our thoughts about a world. We are contingent beings within an already formed world.
Going back to the self-reference, to assert that in effect conceptualism about abstracta is true, one relies on abstracta being in reality, e.g. here that a description or assertion can hold a relationship of accurate description with things as they are. Absent the reality of such a relationship independent of our individual or collective concepts, truth is meaningless. If only the concrete exists in reality, truth, an abstract relationship using symbolic representation (other abstracta!) is a case of non-being, illusion. Actually, illusion is another abstract relationship. Meaninglessness is next up, but this too is an abstract state of affairs. The infinite regress of abstracta begging to be acknowledged as real yawns open.
The reality of core abstracta is inescapably the case, i.e. it is necessarily true on pain of not being able to think, communicate conceptually, reason [implication is abstract], speak truth, demonstrate, warrant, know etc.
The serious issue then follows: in what way are such things real?
The best I can answer for now is that such abstracta are connected to the logic of being for worlds or things in the world. They are logically relevant characteristics of being, which in many cases are shared across beings as archetypes that are in-common, or even are in-common across possible worlds. In some cases such as numbers they are in common to all possible worlds as part of the fabric of any distinct possible world.
We may recognise or discover them and try to identify what they precisely are, but in many cases they defy particular definition in words.
Where do they come from, where are they? They come from the logic of being and are embedded as constraints on being. For instance, no entity E is such that it has two core characteristics x and y where y = ~x.
That is why square circles are impossible of being. Regardless of how we may form a fuzzy imagination that oscillates between the shapes or may try to superpose and blend the two.Thus, abstracta are part of the distinct identity, nature and being of any particular entity. That is, the principle of distinct identity has ontological, not just conceptual, significance. That’s why we recognise it as a first principle of right reason.
So, not a spooky, mysterious, metaphysical world of forms, just the architecture of — rational principles or “logic” of — being or possible being (and of impossibility of being). Where of course a considerable part of that embedded architecture of being is structural and quantitative. That is, Mathematical. Mathematics has in key part ontological import. Hence, Wigner’s point on its astonishing power. The music of the spheres is written in the language of mathematics, with — I daresay — Fourier leading the charge.
Speaking of architecture, that does point to architect. But that is an onward discussion tied to the necessary being root of reality. >>
So, what is now on the table is the architecture of — i.e. rational principles or “logic” of — being or possible being or even impossibility of being. Which, in part we may tabulate:

Where also, it is worth the effort to also headline from 375:
KF, 375: >>[W]e can show that key abstract elements of structure and quantity are necessary aspects of the logic of being a distinct possible world.
Consider a distinct possible world, W which is distinct from near neighbours (say W’, W’) by having some aspect of core characteristics A, unique to itself. Were there no A, the world would be indistinguishable from near neighbours and we would recognise that distinct labels have been attached to the same underlying possible world. Such allows us to view W as a structured set:
W = {A|~A}
Now, nothing is in W that is not in A or else ~A, the dichotomy is empty and there is no x in W but not in A or else ~A. This is the quantitative property, nullity; thus zero is present, {} –> 0. Likewise, A is a distinct thing, a unit. Unity is present, so one. Following von Neumann, {0} –> 1, where also A manifests unity. In a different sense, ~A is a complex unity, collecting many other things, pointing to collectives, to systems, to organisation, to function based on organisation etc. For our purposes, ~A is a unit but one different from A, so we need to recognise duality, two-ness, thus two: {0,1} –> 2. Obviously, such succession continues without limit and manifests the naturals, also implying the transfinite ordinals on the premise of order type {0,1,2 . . . } –> w (omega).
Likewise, we may contemplate an inverse such that -x + x –> 0, which is a vector of one dimension. We now have integers. Ratios of integers gives rise to rationals and convergent sums yield the rest of the reals. This gives us continuum. From this, the vector rotation operator i*x repeated twice to give – x allows us to have 2-d vectors in a continuum, a plane. An abstract plane that we may contemplate but which pervades any possible world. Where such a world is sufficiently spatially extended and actualised, we may observe continua, dimensions, vectors, rotations, trajectories etc.
So, we see where any possible world, simply on being distinct, manifests directly 0,1,2 and by extension on the logic of being, N, Z, Q, R, C. The vector phenomenon captured from Z on, allows us to extend the abstract continuum to arbitrarily many dimensions. (Notice the distinction between world manifestations and our extension to n-dimensional entities, n arbitrarily high.In physics we speak of 10^22 degrees of freedom routinely, for statistical thermodynamics, just for a reasonably accessible case.)
Our world manifests three spatial dimensions on the macro scale, and we can observe things like Mobius strips etc.
The underlying point is, that we see intelligible, abstract, necessary, structural and quantitative entities as part of the fabric of any distinct world, part of its framework, part of the logic of its being as a distinct possible world.
In that context, we may identify certain facts of structure and quantity that necessarily obtain.
For instance consider five distinct units and how they may be partitioned into a pair and a triple: ||||| –> || + |||. Obviously, this can be reversed, || + ||| –> |||||. Addition and subtraction have a natural sense of partitioning and combining units. Multiplication and division are extensions as are many onward operations, relations and functions. And so forth.
The point is, that there are abstract, structural and quantitative entities that are intelligible on logic of being which are necessary corollaries of any distinct possible world. These abstracta, we recognise and observe through the effects of the logic of being, we do not invent. They are not merely concepts and constructs we invent and project to a world of things in themselves. That, being in reality just an inner game on the appearances we have and imagine as reflecting the outer world. No, the Kantian ugly gulch fails and we have no good reason to imagine the behaviour of a Mobius strip is some sort of contemplative inner dream. Such dreams we could modify at will, the logic of being is far less yielding than that.
So, we need to frame an understanding of Mathematics that recognises that we may study the logic of structure and quantity, but this is not isolated from the intelligible substance of structure and quantity manifest in the world. Yes, our sense of being and of cause needs to adapt to the logic of being that involves necessary albeit abstract entities. For instance, nullity, the empty set, zero are manifest in a myriad circumstances, indeed in any possible, distinct world. But as {} is indistinguishable from {} there is good reason to see that it is one and the same common entity. Which is a characteristic shown by many abstract entities. >>
So, now, let us further reflect. END