It seems there is now a talking-point agenda to dismiss the fine tuning issue as an illusion.
So, in the current thread on the big bang and fine tuning, I have clipped and commented on a recent article by Luke Barnes.
However, comments cannot put up images [save through extraordinary steps], so it is first worth showing Barnes’ key illustration, as showing where fine tuning comes in, updating Hoyle’s remark about the C-O balance first key fine tuning issue put on the table in 1953:
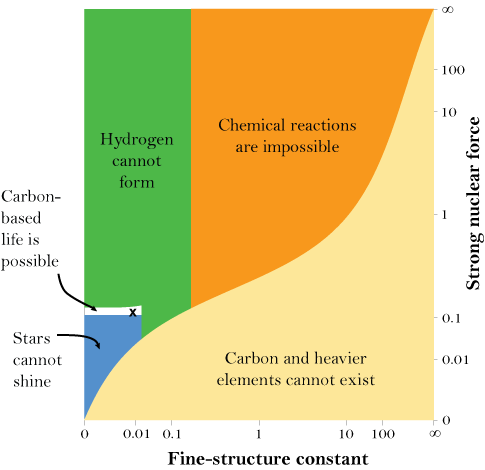
>>Luke Barnes has a useful semi-pop summary:
http://www.thenewatlantis.com/…..tures-laws
Today, our deepest understanding of the laws of nature is summarized in a set of equations. Using these equations, we can make very precise calculations of the most elementary physical phenomena, calculations that are confirmed by experimental evidence. But to make these predictions, we have to plug in some numbers that cannot themselves be calculated but are derived from measurements of some of the most basic features of the physical universe. These numbers specify such crucial quantities as the masses of fundamental particles and the strengths of their mutual interactions. After extensive experiments under all manner of conditions, physicists have found that these numbers appear not to change in different times and places, so they are called the fundamental constants of nature.
These constants represent the edge of our knowledge. Richard Feynman called one of them — the fine-structure constant, which characterizes the amount of electromagnetic force between charged elementary particles like electrons — “one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man.” An innovative, elegant physical theory that actually predicts the values of these constants would be among the greatest achievements of twenty-first-century physics.
Many have tried and failed. The fine-structure constant, for example, is approximately equal to 1/137, a number that has inspired a lot of worthless numerology, even from some otherwise serious scientists. Most physicists have received unsolicited e-mails and manuscripts from over-excited hobbyists that proclaim, often in ALL CAPS and using high-school algebra, to have unlocked the mysteries of the universe by explaining the constants of nature.
Since physicists have not discovered a deep underlying reason for why these constants are what they are, we might well ask the seemingly simple question: What if they were different? What would happen in a hypothetical universe in which the fundamental constants of nature had other values?
There is nothing mathematically wrong with these hypothetical universes. But there is one thing that they almost always lack — life. Or, indeed, anything remotely resembling life. Or even the complexity upon which life relies to store information, gather nutrients, and reproduce. A universe that has just small tweaks in the fundamental constants might not have any of the chemical bonds that give us molecules, so say farewell to DNA, and also to rocks, water, and planets. Other tweaks could make the formation of stars or even atoms impossible. And with some values for the physical constants, the universe would have flickered out of existence in a fraction of a second. That the constants are all arranged in what is, mathematically speaking, the very improbable combination that makes our grand, complex, life-bearing universe possible is what physicists mean when they talk about the “fine-tuning” of the universe for life.
That’s the issue in broad overview, from one angle.
Barnes adds some details that we can ponder for a moment:
. . . we can calculate all the ways the universe could be disastrously ill-suited for life if the masses of these [fundamental] particles were different. For example, if the down quark’s mass were 2.6 x 10-26 grams or more, then adios, periodic table! There would be just one chemical element and no chemical compounds, in stark contrast to the approximately 60 million known chemical compounds in our universe.
With even smaller adjustments to these masses, we can make universes in which the only stable element is hydrogen-like. Once again, kiss your chemistry textbook goodbye, as we would be left with one type of atom and one chemical reaction. If the up quark weighed 2.4 x 10-26 grams, things would be even worse — a universe of only neutrons, with no elements, no atoms, and no chemistry whatsoever.
The universe we happen to have is so surprising under the Standard Model because the fundamental particles of which atoms are composed are, in the words of cosmologist Leonard Susskind, “absurdly light.” Compared to the range of possible masses that the particles described by the Standard Model could have, the range that avoids these kinds of complexity-obliterating disasters is extremely small. Imagine a huge chalkboard, with each point on the board representing a possible value for the up and down quark masses. If we wanted to color the parts of the board that support the chemistry that underpins life, and have our handiwork visible to the human eye, the chalkboard would have to be about ten light years (a hundred trillion kilometers) high.
And that’s just for the masses of some of the fundamental particles. There are also the fundamental forces that account for the interactions between the particles. The strong nuclear force, for example, is the glue that holds protons and neutrons together in the nuclei of atoms. If, in a hypothetical universe, it is too weak, then nuclei are not stable and the periodic table disappears again. If it is too strong, then the intense heat of the early universe could convert all hydrogen into helium — meaning that there could be no water, and that 99.97 percent of the 24 million carbon compounds we have discovered would be impossible, too. And, as the chart to the right shows, the forces, like the masses, must be in the right balance. If the electromagnetic force, which is responsible for the attraction and repulsion of charged particles, is too strong or too weak compared to the strong nuclear force, anything from stars to chemical compounds would be impossible.
Stars are particularly finicky when it comes to fundamental constants. If the masses of the fundamental particles are not extremely small, then stars burn out very quickly. Stars in our universe also have the remarkable ability to produce both carbon and oxygen, two of the most important elements to biology. But, a change of just a few percent in the up and down quarks’ masses, or in the forces that hold atoms together, is enough to upset this ability — stars would make either carbon or oxygen, but not both.
And more.
This is not an illusion, it is a significant point.
And, Robin Collins aptly used the concept of a bread factory. A super-physics that forces these constants to a just-right range would be like how a factory has to be in a Goldilocks just-right zone to bake good loaves.
In short, pushing up the fine tuning one level does not get rid of it.
And a bread factory bakes a LOT of loaves, so if we have it randomly tuned, if the just right zone is not broad and easily found on a well behaved fitness slope, then things begin to get tricky: we should not be at this sort of deeply isolated operating point. That is, John Leslie was right, locally isolated operating points are like the lone fly on the patch of wall swatted by a bullet. Matters not that other stretches may be carpeted and any bullet would hit a fly.
In this zone, there’s the one fly. Crack-splat.
Tack-driver rifles and marksmen capable of using that capability don’t come along just so. Just ask Olympics champs about their training regimes and rifles.
Then, take a look at how the AR-15 family has evolved by design to take up features of such rifles. (Then ask how such a rifle would work at 1,000 m.)>>
This is of course FYI-FTR, so comments will be entertained back on the original thread. END
PS: An earlier UD post on fine tuning, here, gives useful background including links to more detailed discussions and answers to significant objections.