“What is time?” is a misleadingly simple question, one that soon surfaces many difficulties. That is, it is a philosophical issue: phil, being the study of hard big questions. However, it is clear that we need to ponder it here at UD at least at a basic level, if we are to examine relevant concerns such as cosmological fine tuning and the evident beginning of the observed cosmos in a singularity, currently typically projected as about 13.8 billion years ago . . . the following chart based on WIMAP has 13.77 BYA and starts with “quantum fluctuations” leading to a super-luminous stretching of space called inflation:
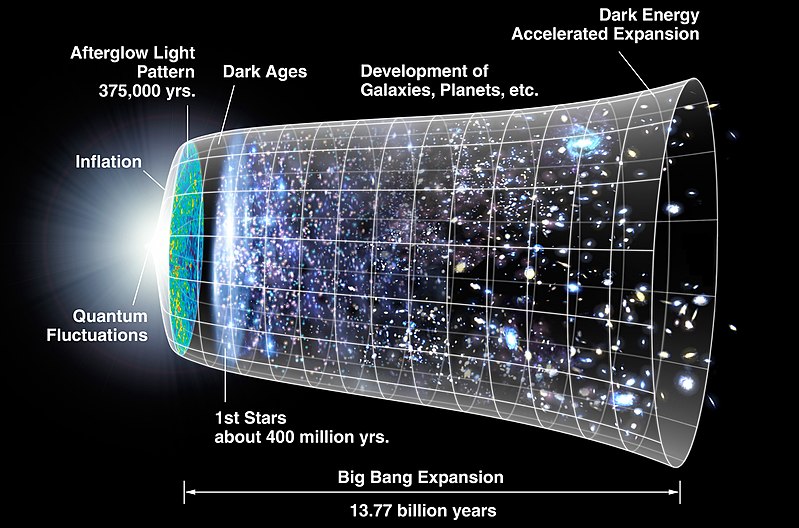
However, we still have not yet resolved the question at even first level. A good start (we must encourage the Wikipedians when they do reasonably well) is this from Wiki:
Time is the indefinite continued progress of existence and events that occur in apparently irreversible succession through the past, in the present, and the future. Time is a component quantity of various measurements used to sequence events, to compare the duration of events or the intervals between them, and to quantify rates of change of quantities in material reality or in the conscious experience. Time is often referred to as a fourth dimension, along with three spatial dimensions.
Time has long been an important subject of study in religion, philosophy, and science, but defining it in a manner applicable to all fields without circularity has consistently eluded scholars. Nevertheless, diverse fields such as business, industry, sports, the sciences, and the performing arts all incorporate some notion of time into their respective measuring systems.
Time in physics is unambiguously operationally defined as “what a clock reads”.
(HT: Wiki, links and footnotes omitted)
What a clock reads is a key clue.
For, it points to causal-temporal succession, thus to enabling energy flows from regions of concentration that allow orderly forced motion (i.e. physical work) thus apparently regular oscillations — cyclical, repeated hopefully regular processes — that can be accumulated as a local index of the passage of time, e.g. through a watch:

This immediately brings out the famed “arrow of time,” entropy.
For, a key driving force behind a process is the flow of energy from zones of high concentration (thus, high order or organisation or at least high temperatures serving as heat reservoirs for heat engines) through systems and processes to heat sinks.
That is, time is closely connected to thermodynamics, and onwards to the projected heat death of the observed cosmos (considered as a thermodynamically isolated system). Wiki also has a useful summary on heat death, which I will clip:
The heat death of the universe, also known as the Big Chill or Big Freeze,[1] is an idea of an ultimate fate of the universe in which the universe has evolved to a state of no thermodynamic free energy and therefore can no longer sustain processes that increase entropy. Heat death does not imply any particular absolute temperature; it only requires that temperature differences or other processes may no longer be exploited to perform work. In the language of physics, this is when the universe reaches thermodynamic equilibrium (maximum entropy).
If the topology of the universe is open or flat, or if dark energy is a positive cosmological constant (both of which are consistent with current data), the universe will continue expanding forever, and a heat death is expected to occur,[2] with the universe cooling to approach equilibrium at a very low temperature after a very long time period.
The hypothesis of heat death stems from the ideas of William Thomson, 1st Baron Kelvin (Lord Kelvin), who in the 1850s took the theory of heat as mechanical energy loss in nature (as embodied in the first two laws of thermodynamics) and extrapolated it to larger processes on a universal scale.
In short, if the cosmos is an isolated system (no mass, energy or information passes into or out of it) then it is headed for a point where as energy resources have been dissipated, significant physical change [that requiring energy concentrations to drive work] ceases, clocks cease and effectively time itself considered as what clocks measure ceases. Clocks are no longer possible, as would be biological processes and ecosystems or computational processes etc. For, constructive work has ceased for want of energy concentrations and heat sinks to drive it. (As opposed to random particle motion or trajectories etc.)
The thermodynamics of heat engines is king, in short:
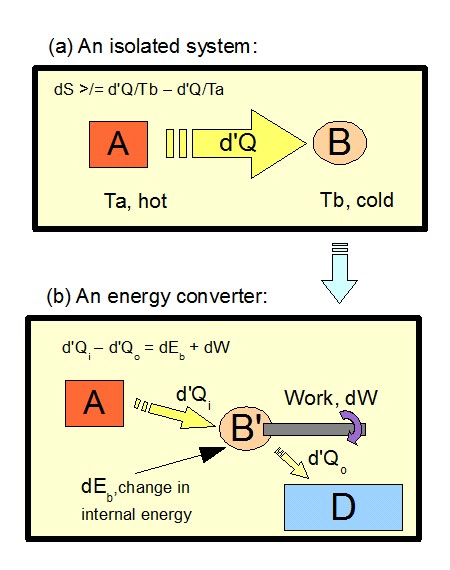
This directly speaks to the proposed infinite past (on the speculation that the big bang represents a fluctuation or the like in a wider cosmos as a whole). For, in transfinite time, any finite reservoir of high quality, concentrated energy will be exhausted. And if one proposes an infinite reservoir in the macro-cosmos, then that requires an equally infinite sink, or else the overall entity will cook itself into a high temperature heat death. Nor do random fluctuations seem to be plausible candidates for creating random pools of order on the scope of our observed cosmos. (Indeed, we would overwhelmingly expect to see a Boltzmann Brain micro-cosmos or the like, rather than the sort of extended entity we see. On a fluctuation, poof, such a brain which perceives a world then poof, gone.)
In this context, Sean Carroll of Caltech is interesting:
I’m trying to understand how time works. And that’s a huge question that has lots of different aspects to it. A lot of them go back to Einstein and spacetime and how we measure time using clocks. But the particular aspect of time that I’m interested in is the arrow of time: the fact that the past is different from the future. We remember the past but we don’t remember the future. There are irreversible processes. There are things that happen, like you turn an egg into an omelet, but you can’t turn an omelet into an egg.
And we sort of understand that halfway. The arrow of time is based on ideas that go back to Ludwig Boltzmann, an Austrian physicist in the 1870s. He figured out this thing called entropy. Entropy is just a measure of how disorderly things are. And it tends to grow. That’s the second law of thermodynamics: Entropy goes up with time, things become more disorderly. So, if you neatly stack papers on your desk, and you walk away, you’re not surprised they turn into a mess. You’d be very surprised if a mess turned into neatly stacked papers. That’s entropy and the arrow of time. Entropy goes up as it becomes messier.
So, Boltzmann understood that and he explained how entropy is related to the arrow of time. But there’s a missing piece to his explanation, which is, why was the entropy ever low to begin with? Why were the papers neatly stacked in the universe? Basically, our observable universe begins around 13.7 billion years ago in a state of exquisite order, exquisitely low entropy. It’s like the universe is a wind-up toy that has been sort of puttering along for the last 13.7 billion years and will eventually wind down to nothing. But why was it ever wound up in the first place? Why was it in such a weird low-entropy unusual state?
That is what I’m trying to tackle. I’m trying to understand cosmology, why the Big Bang had the properties it did. And it’s interesting to think that connects directly to our kitchens and how we can make eggs, how we can remember one direction of time, why causes precede effects, why we are born young and grow older. It’s all because of entropy increasing. It’s all because of conditions of the Big Bang.
He goes on to discuss multiverse models (note, here, that the Boltzmann brain type fluctuation will utterly dominate such models):
If you find an egg in your refrigerator, you’re not surprised. You don’t say, “Wow, that’s a low-entropy configuration. That’s unusual,” because you know that the egg is not alone in the universe. It came out of a chicken, which is part of a farm, which is part of the biosphere, etc., etc. But with the universe, we don’t have that appeal to make. We can’t say that the universe is part of something else. But that’s exactly what I’m saying. I’m fitting in with a line of thought in modern cosmology that says that the observable universe is not all there is. It’s part of a bigger multiverse. The Big Bang was not the beginning.
And if that’s true, it changes the question you’re trying to ask. It’s not, “Why did the universe begin with low entropy?” It’s, “Why did part of the universe go through a phase with low entropy?”
(Notice, how a highly speculative suggestion has been used as though it had the kind of observational support that backs the singularity. And, notice, how the Boltzmann brain domination of such fluctuation models is not headlined. Indeed, Boltzmann comes up multiple times in the interview but Boltzmann brain is not mentioned. Nor is there an evaluation of implications of entropy for the very long term in a supposedly infinite duration quasi-physical cosmos. Such exemplifies how science can sometimes slide into philosophy without a proper comparative difficulties evaluation; inadvertently begging big questions.)
Let me use Wiki speaking against its general ideological bent:
a Boltzmann brain is a self-aware entity that arises due to extremely rare random fluctuations out of a state of thermodynamic equilibrium [–> the predominant, statistically overwhelming group of accessible micro-states for a relevant entity in statistical thermodynamics]. For example, in a homogeneous Newtonian soup, theoretically by sheer chance all the atoms could bounce off and stick to one another in such a way as to assemble a functioning human brain (though this would, on average, take vastly longer than the current lifetime of the universe). The idea is indirectly named after the Austrian physicist Ludwig Boltzmann (1844–1906), who in 1896 published a theory that the Universe is observed to be in a highly improbable non-equilibrium state because only when such states randomly occur can brains exist to be aware of the Universe. One criticism of Boltzmann’s “Boltzmann universe” hypothesis is that the most common thermal fluctuations are as close to equilibrium overall as possible; thus, by any reasonable criterion, human brains in a Boltzmann universe with myriad neighboring stars would be vastly outnumbered by “Boltzmann brains” existing alone in an empty universe.
Boltzmann brains gained new relevance around 2002, when some cosmologists started to become concerned that, in many existing theories about the Universe, human brains in the current Universe appear to be vastly outnumbered by Boltzmann brains in the future Universe who, by chance, have exactly the same perceptions that we do; this leads to the absurd conclusion that statistically we ourselves are likely to be Boltzmann brains. Such a reductio ad absurdum argument is sometimes used to argue against certain theories of the Universe. When applied to more recent theories about the multiverse, Boltzmann brain arguments are part of the unsolved measure problem of cosmology.
Coming back, you may notice that clocks measure local time. This reflects relativity, where velocity and separation affect perceived simultaneity and the perceived lapse of time. That is a significant issue, but it does not remove the validity of the temporal-causal succession macro-scale view of time.
In this context, a significant discussion on a suggested infinite in the past macro-cosmos arose in a prior thread on hyperreals, infinitesimals etc.
To set context, allow me to show the surreals panorama in which the reals appear after w steps of construction, as the first vertical bar, with the integers as mileposts:
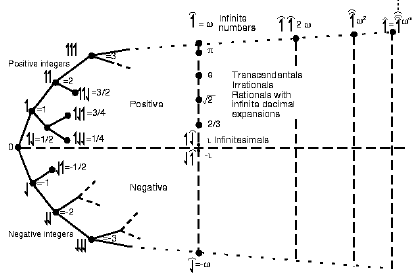
Likewise, following Dr Carol Wood, we may identify a hyperreal, K such that 1/K is an infinitesimal, which I have termed m:
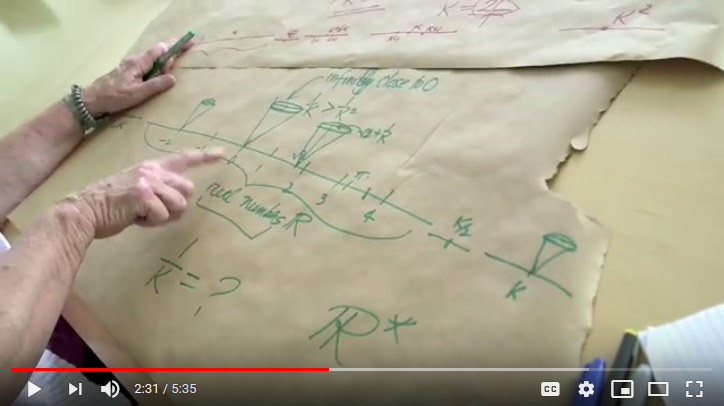
I add, showing descent from K in *N in unit steps (which will not attain to a finite span from 0, indicating the power of the ellipsis beyond n in N:
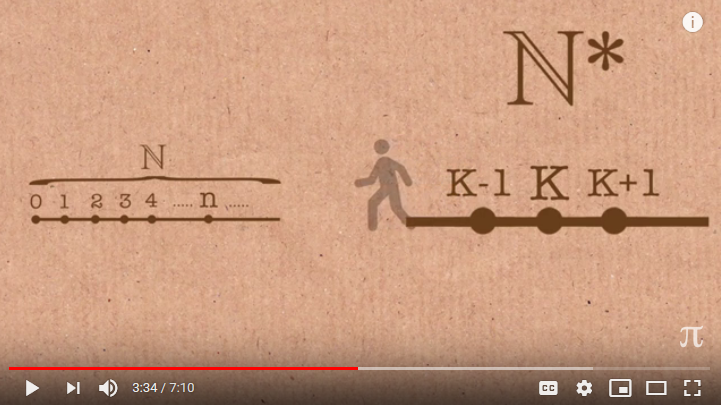
I clip here a comment I made in the discussion (which I hope is helpful to those troubled by infinite past within the reals claims):
KF, 165: >> there is no definable last finite integer ranging out L-wards step by step from 0 [–> in effect, 0, -1, -2 . . . -k, -(k+1) . . . without limit where k is any arbitrary typically large (and finite! . . . note, bound by k+1), particular distinct natural number we may symbolise]. Likewise, there is no definable least transfinite descending K, K-1, K-2, . . . K/2, . . . which is mirrored on the L-ward side, just harder to represent. [–> Here, K is a hyperreal so that 1/K = m, an infinitesimal closer to 0 than 1/k = n, for any k in the naturals, N.) We have a fuzzy border lurking under the seemingly simple ellipsis.
Take the hyperbolic 1/x catapult down towards 0 and we have -m = 1/-K which is closer to zero than 1/-k for any -k in Z-. Shift the resulting infinitesimal cloud anywhere along the reals, to r in R. [Just add 0 + cloud to r.] There is no definable closest real to r, part of there being a continuum. Also, there are hyperreals yet closer to r than any neighbouring real. The fuzzy border phenomenon appears around every real.
Coming back, I already wrote to you:
Z- never begins: { . . . -2, -1, 0} but that’s the point. To get to -2 temporally [considering the past stages as labelled with numbers for convenience] you have to descend down the full beginningless span of that ellipsis. Where for every stage Q finitely removed from -2, {. . . Q, . . . -2, -1, 0} you have had to descend to Q-2, Q-1, i,e, the chain replicates L-wards beyond Q in direct copy of to 0, i.e. the span is demonstrably infinite L-wards. And EVERY Q takes in the claim that the whole chain L-wards comprises finite values so that Q is bound by Q-1 for every Q in Z-. The chain is indeed beginningless L-wards in the sense of infinite.
In short we can do an L-wards 1:1 for every Q in Z-:
{. . . Q-2, Q-1, Q}
{ . . . -2, -1, 0}That is we see a self-similar copy of Z- appearing L-wards at every Q, i.e. the set is infinite L-wards. This is sledgehammer to peanut.
There is no identifiable L-wards first element of Z-, that’s what we ALL know the ellipsis means, and that therefore every identifiable Q in Z- is bound by an indefinite onward extension L-wards.
It is the consequence of this when we apply it to succession of temporal-causal stages approaching to Q from L-wards going R-wards that the significance appears. From Q L-wards, we have a copy L-shifted of from 0 L-wards, i.e. the order type of the succession L-wards from Q is w, of cardinality aleph null. We have not got away from the supertask of descent down a transfinite span, we still face it. Such a span cannot be bridged going R-wards to approach Q no more than it can be spanned going R-wards from 0.
This is the familiar supertask of spanning the transfinite in steps.
Going further, an argument that in effect holds that at every Q in Z- that is in finite span of 0 [having been constructed in the set builder sense by mirror image of the von Neumann construction] is a stage where the L-wards transfinite has already been spanned so is not a problem, fails.Fails by begging the question at issue. Spanning an actual past of step by step successive stages from a “beginningless” past.
We find here no warrant for begging or setting the question aside.
We are only warranted to address finitely remote past points Q that do not involve an antecedent transfinite span to Q.Credibly, there was no beginningless past that advanced by successive cumulative stages to the present.
Such a claim would require a supertask essentially similar to descent to now from a defined transfinitely remote stage, -K.>>
Going beyond, for example there is the famous A vs B theory debate: rather roughly, on the A view there is NOW, which progresses so that the past has gone and does not exist as such, it is an abstraction (albeit one that thanks to cause has marked the present) just as is the future. Here, unidirection of cause is such that the actual future cannot act causally in the now, it is its not yet emerged result. The B theory is more perspectival, seeing time as a panorama and our present as our particular for the moment point of view. In effect, events of a certain famous weekend in 30 AD just outside Jerusalem are just as real (but “past-wards” — strictly, “earlier than” — from us) as is our now this Easter Sunday, and as is the as yet unperceived future (strictly “later than”). And of course, the onward obvious point is: are there forks so there are multidimensional temporal timelines . . . a significant view in Quantum Mechanics. Nor should we overlook relativistic effects yielding the locality of now-ness. What is “now” for The Andromeda Galaxy, 2+ mn light years away, or for a Quasar at the edge of our observable cosmos, or on the brink of a black hole’s event horizon? Or, for the planet-wide array of telescopes we are using to try to observe and image it, here, the one in M87?

Huge, hotly debated issues hinge on the implications and challenges embedded in these views. In short, time is a pivotal, foundational concept.
There is of course much more to time, but the above is enough to spark thought onwards. END
PS: Carlo Rovelli before the UK’s Royal Institution on time i/l/o quantum gravity: