Here:
This syllogism is of considerable practical importance:

This raises the issue of denying the consequent, ~q. If p –> q and ~q, then as q is necessary for p, ~p. Where, p is sufficient for q, by reason of its core characteristics, the states of affairs associated with p, causal power, requirement of logic of being etc.
Let us note, p –> q is equivalent in import to ~q –> ~p.
(Let’s add, that denying the antecedent, thinking this falsifies the consequent also fails, p –> q does not mean there isn’t another way, say r, to get q. There’s more than one way to skin a cat-fish.)
Connected to ID, Newton’s rules demand that causal adequacy be shown before assigning powers to claimed causes, especially for things we cannot directly observe. (Design [= intelligently directed configuration] routinely causes functionally specific, complex organisation and/or associated information beyond 500 – 1,000 bits. Undirected, blind dynamic-stochastic processes . . . chance and/or mechanical necessity alone . . . have no such observed powers. Hence the controversial resort to Lewontin’s a priori commitment to only allow materialistic causes.)
Dynamic-stochastic process:
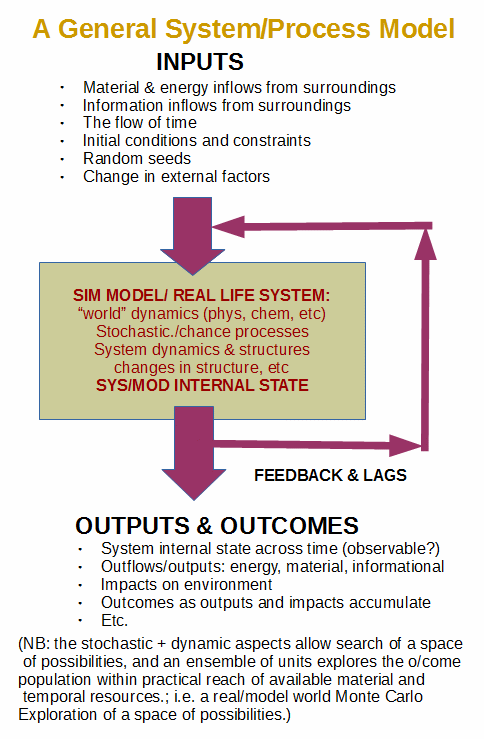
As it just came up again, let me again document how the ID explanatory filter does not impose design as a default but instead infers across three broad explanatory forces, blind chance and/or mechanical necessity and/or design . . . and yes all three factors can be jointly at work so we need to examine an entity, network, structure or process per aspect:
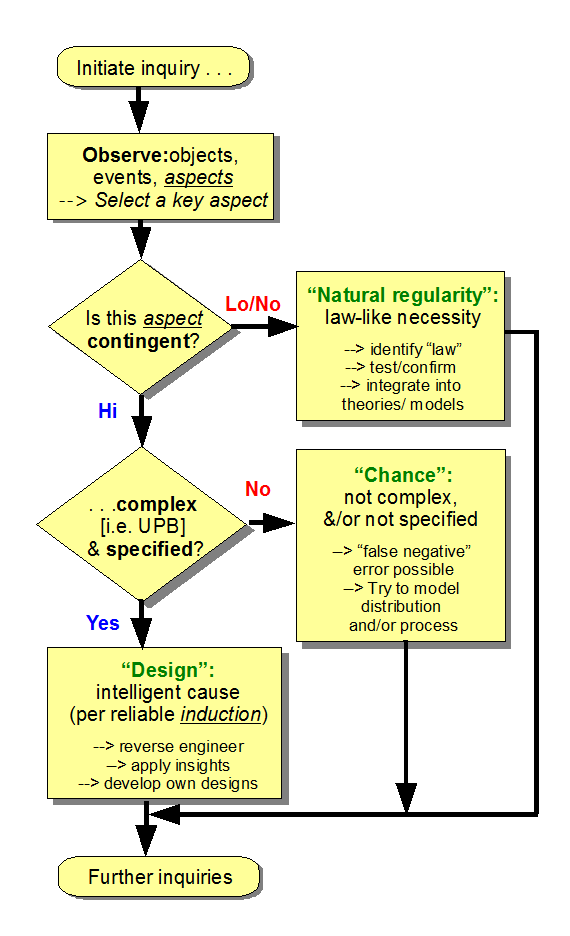
We thus see modus ponens [direct implication] and modus tollens [denial of the consequent]. A classic application of the latter, is that once a chain of implications terminates in a falsehood, this upends the chain. This is used in proof by reductio ad absurdum.
Related, p –> q and q –> r entails, p –> r, which extends to any chain we may warrant. That is, truth of an initial proposition chains downstream. This truth transmission property is an important power of implication.
Bearing in mind that time may be a factor in causal chains, cause-effect bonds, likewise, will flow from initial conditions to outcome. Hence, the issue of a first-cause agent, something which is self-moved and initiates chains of consequences. To type, I move a finger to and press a key initiating a keyboard scan and ultimately screen display, etc.
This points to the explanation argument, inference to the best explanation, aka abductive reasoning. (Abductive reasoning also includes the educated guesswork of spotting candidate patterns, hypothesis creation.)
The idea here is that facts of observation f1, f2, . . . fn = F, require a common explanation, so, we have candidate explanations e1, e2 . . . em that can be tested for implying the span of facts F. We also look for coherence and for balanced explanatory power [neither an ad hoc patchwork nor simplistic], picking the best, where E –> F. Power to predict future facts is a further important test. Such explanations, are not proved, nor can abduction — an inductive form of reasoning — prove, though it can support high reliability in a tested zone of application. However, implications are such that a false explanation or model can also be highly reliable.
Underneath, is the meaning of IF — THEN –, that is sufficiency:
p –> q is equivalent to ~ [p AND ~q], we cannot have p true and q false. This does not mean, p is true. To get there, we would need EQUIVALENCE, i.e. p –> q and q –> p. That is p is necessary and sufficient for q. The fallacy of affirming the consequent confuses p –> q with that equivalence.
Linked, q is necessary for p, that is, ~p OR q. This can be shown by using truth tables for what is called material implication.
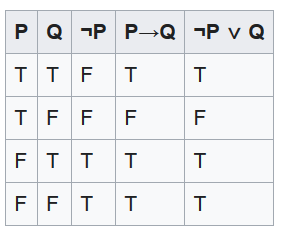
Hence, the peculiar phrase for equivalence, “necessary and sufficient.” In Mathematical contexts, we may see p IFF q, p if and only if q. Notice, a false p can properly imply a true q, which is a subtlety that is the root of many errors of thought.
Also related, is the disjunctive syllogism:

The conjunctive syllogism is p AND q, so that for and to be true both must be. This can be chained, and of course we then see if a chain has in it x and y so y = ~x, then the whole is inconsistent logically. One use of this is in a coherence defence by augmenting explanation. If claims p1, p2, . . . pn = P are suspected to be inconsistent but on augmenting with some e, e AND P is coherent, P must be coherent. This is the heart of Plantinga’s free will defence of the coherence of the concept of God in ethical theism. It also allows us to see that we can for example make a coherent account of the passion-resurrection narratives in the gospels. Weakening, to the case where there are contradictions, we may be able to identify which of x or y to choose, or we may be able to footnote the matter and set it aside as a difficulty. In short, it can be very hard to demonstrate substantial and irretrievable inconsistency in a string of propositions forming a narrative.
The celebrated case of the six blind men of Hindustan encountering the elephant and having partial patterns (beloved of post modernists and those who try to reduce differences to relativism), is a subtle lesson:

The onlooker with a broader picture and better explanation illustrates the power of a best explanation. Notice, here, it is Jesus of Nazareth!
Such various real-world syllogisms, however, are important.
In particular, implication used for explanation or prediction has utility in planning or modelling. We propose a “simplified” or proposed or candidate, p and explore its implications or what it explains. We may look at several, then choose the best, which we then implement.
In short, the logic of implication is powerful, subtle, useful but a source of many pitfalls. We would to well to study it. END